Question Number 132594 by Study last updated on 15/Feb/21

Commented by mr W last updated on 15/Feb/21
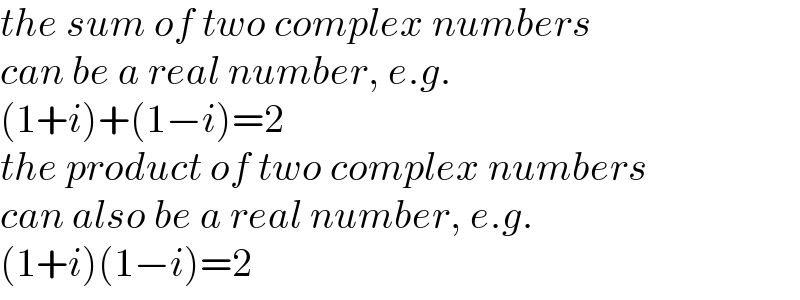
$${the}\:{sum}\:{of}\:{two}\:{complex}\:{numbers} \\ $$$${can}\:{be}\:{a}\:{real}\:{number},\:{e}.{g}.\: \\ $$$$\left(\mathrm{1}+{i}\right)+\left(\mathrm{1}−{i}\right)=\mathrm{2} \\ $$$${the}\:{product}\:{of}\:{two}\:{complex}\:{numbers} \\ $$$${can}\:{also}\:{be}\:{a}\:{real}\:{number},\:{e}.{g}.\: \\ $$$$\left(\mathrm{1}+{i}\right)\left(\mathrm{1}−{i}\right)=\mathrm{2} \\ $$
Answered by liberty last updated on 15/Feb/21
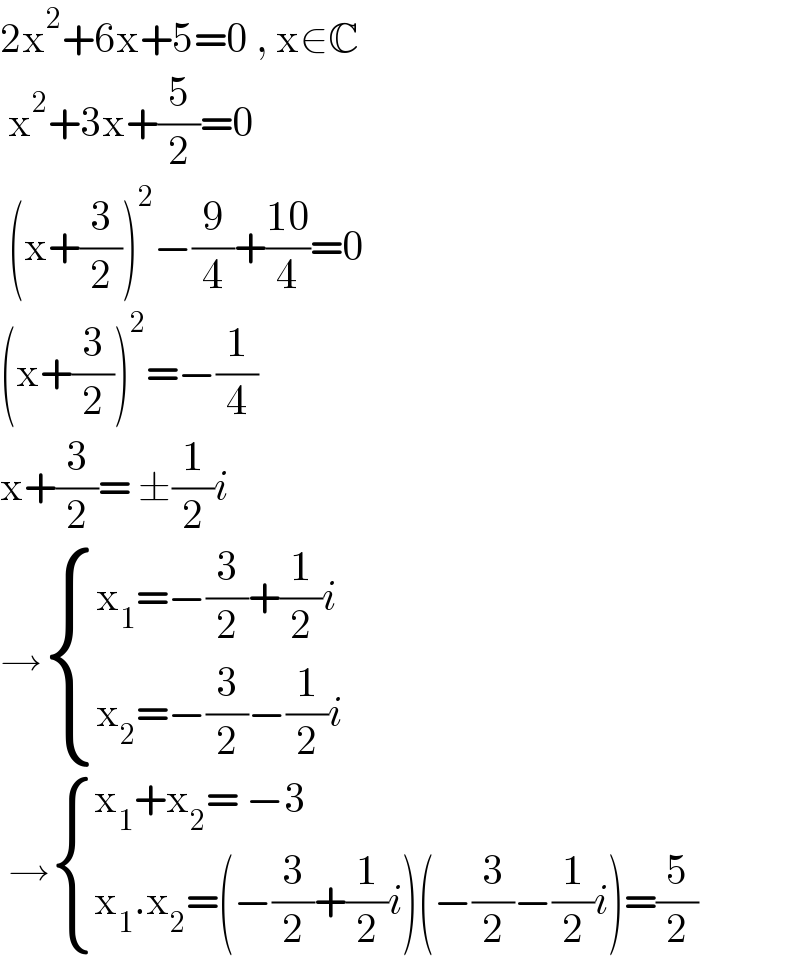
$$\mathrm{2x}^{\mathrm{2}} +\mathrm{6x}+\mathrm{5}=\mathrm{0}\:,\:\mathrm{x}\in\mathbb{C} \\ $$$$\:\mathrm{x}^{\mathrm{2}} +\mathrm{3x}+\frac{\mathrm{5}}{\mathrm{2}}=\mathrm{0} \\ $$$$\:\left(\mathrm{x}+\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{9}}{\mathrm{4}}+\frac{\mathrm{10}}{\mathrm{4}}=\mathrm{0} \\ $$$$\left(\mathrm{x}+\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{x}+\frac{\mathrm{3}}{\mathrm{2}}=\:\pm\frac{\mathrm{1}}{\mathrm{2}}{i} \\ $$$$\rightarrow\begin{cases}{\mathrm{x}_{\mathrm{1}} =−\frac{\mathrm{3}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}{i}}\\{\mathrm{x}_{\mathrm{2}} =−\frac{\mathrm{3}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}{i}}\end{cases} \\ $$$$\:\rightarrow\begin{cases}{\mathrm{x}_{\mathrm{1}} +\mathrm{x}_{\mathrm{2}} =\:−\mathrm{3}}\\{\mathrm{x}_{\mathrm{1}} .\mathrm{x}_{\mathrm{2}} =\left(−\frac{\mathrm{3}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}{i}\right)\left(−\frac{\mathrm{3}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}{i}\right)=\frac{\mathrm{5}}{\mathrm{2}}}\end{cases} \\ $$
