Question-132809

Question Number 132809 by mr W last updated on 17/Feb/21

Commented by mr W last updated on 18/Feb/21

a mountain has the shape of a right circular cone as shown (h>(√3)r). from point A to point B two sightseeing roads one time around the mountain should be built: road I with the shortest length. road II with a constant slope. 1. find the lengthes of both roads. 2. do the both roads cross in the middle? if yes, where?

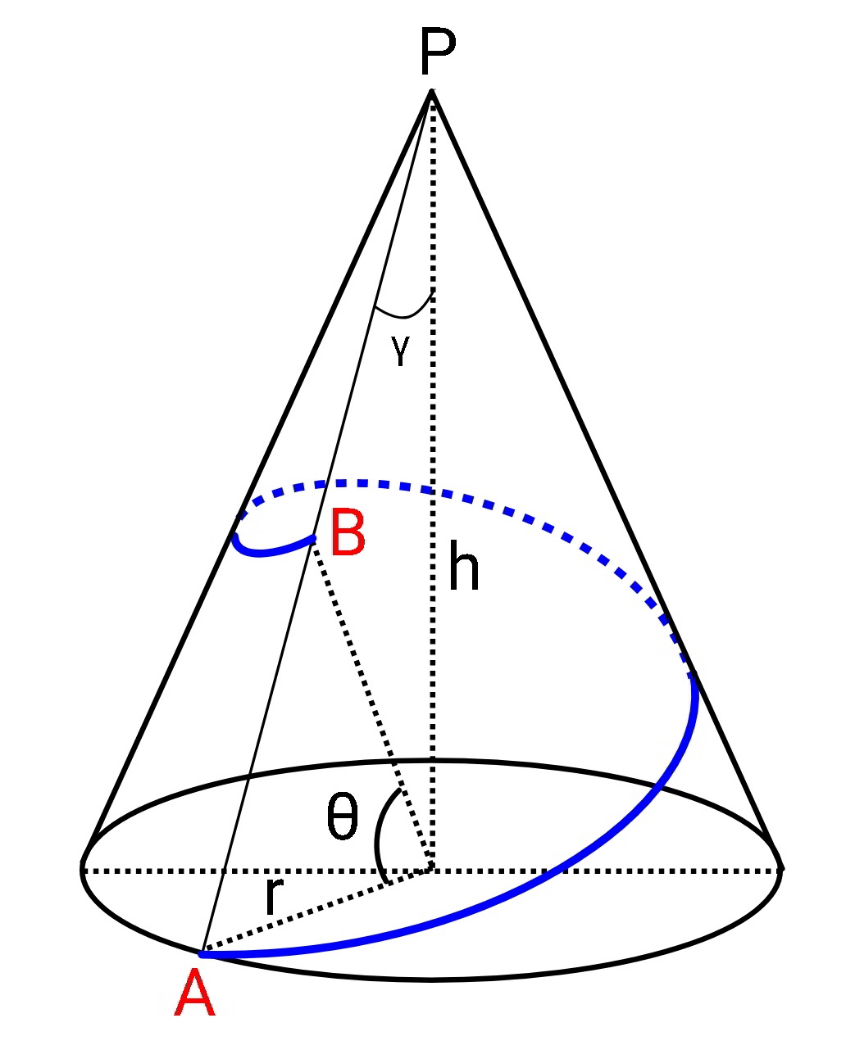
$${a}\:{mountain}\:{has}\:{the}\:{shape}\:{of}\:{a}\:{right} \\ $$$${circular}\:{cone}\:{as}\:{shown}\:\left({h}>\sqrt{\mathrm{3}}{r}\right). \\ $$$${from}\:{point}\:{A}\:{to}\:{point}\:{B}\:{two} \\ $$$${sightseeing}\:{roads}\:{one}\:{time}\:{around} \\ $$$${the}\:{mountain}\:{should}\:{be}\:{built}: \\ $$$${road}\:{I}\:{with}\:{the}\:{shortest}\:{length}. \\ $$$${road}\:{II}\:{with}\:{a}\:{constant}\:{slope}. \\ $$$$\mathrm{1}.\:{find}\:{the}\:{lengthes}\:{of}\:{both}\:{roads}. \\ $$$$\mathrm{2}.\:{do}\:{the}\:{both}\:{roads}\:{cross}\:{in}\:{the}\:{middle}? \\ $$$${if}\:{yes},\:{where}? \\ $$

Commented by bramlexs22 last updated on 17/Feb/21

sθ = 2πr ⇒θ = ((2πr)/s) ; s = (√(r^2 +h^2 )) θ = ((2πr)/( (√(r^2 +h^2 )))) . let AB = x AB^2 = (s−x)^2 +s^2 −2s.(s−x)cos (((2πr)/( (√(r^2 +h^2 )))))

$$\mathrm{s}\theta\:=\:\mathrm{2}\pi\mathrm{r}\:\Rightarrow\theta\:=\:\frac{\mathrm{2}\pi\mathrm{r}}{\mathrm{s}}\:;\:\mathrm{s}\:=\:\sqrt{\mathrm{r}^{\mathrm{2}} +\mathrm{h}^{\mathrm{2}} } \\ $$$$\theta\:=\:\frac{\mathrm{2}\pi\mathrm{r}}{\:\sqrt{\mathrm{r}^{\mathrm{2}} +\mathrm{h}^{\mathrm{2}} }}\:.\:\mathrm{let}\:\mathrm{AB}\:=\:\mathrm{x}\: \\ $$$$\:\mathrm{AB}^{\mathrm{2}} \:=\:\left(\mathrm{s}−\mathrm{x}\right)^{\mathrm{2}} +\mathrm{s}^{\mathrm{2}} −\mathrm{2s}.\left(\mathrm{s}−\mathrm{x}\right)\mathrm{cos}\:\left(\frac{\mathrm{2}\pi\mathrm{r}}{\:\sqrt{\mathrm{r}^{\mathrm{2}} +\mathrm{h}^{\mathrm{2}} }}\right) \\ $$$$ \\ $$

Commented by mr W last updated on 17/Feb/21

$${this}\:{is}\:{for}\:{road}\:{I}.\:{thanks}! \\ $$$${give}\:{also}\:{a}\:{try}\:{for}\:{road}\:{II}\:? \\ $$

Commented by ajfour last updated on 17/Feb/21

need to know- how the ′slope′ in ′constant slope′ is defined; two options, i think: (dz/(rdθ)) (dz≠dl) ; r=(√(x^2 +y^2 )) OR (dz/( (√((rdθ)^2 +(dl)^2 )))) ; l=(√(x^2 +y^2 +(h−z)^2 ))

$${need}\:{to}\:{know}-\:{how}\:{the}\:'{slope}'\:{in} \\ $$$$'{constant}\:{slope}'\:{is}\:{defined}; \\ $$$${two}\:{options},\:{i}\:{think}: \\ $$$$\frac{{dz}}{{rd}\theta}\:\:\:\:\left({dz}\neq{dl}\right)\:;\:\:{r}=\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:\:\:\:{OR} \\ $$$$\frac{{dz}}{\:\sqrt{\left({rd}\theta\right)^{\mathrm{2}} +\left({dl}\right)^{\mathrm{2}} }}\:\:;\:\:{l}=\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\left({h}−{z}\right)^{\mathrm{2}} } \\ $$$$ \\ $$

Commented by mr W last updated on 17/Feb/21

definition of slope: from (x,y,z) to (x+Δx,y+Δh,z+Δz) slope=((Δz)/( (√((Δx)^2 +(Δy)^2 ))))=((Δz)/( (√((Δl)^2 −(Δz)^2 )))) with Δl=(√((Δx)^2 +(Δy)^2 +(Δz)^2 ))

$${definition}\:{of}\:{slope}: \\ $$$${from}\:\left({x},{y},{z}\right)\:{to}\:\left({x}+\Delta{x},{y}+\Delta{h},{z}+\Delta{z}\right) \\ $$$${slope}=\frac{\Delta{z}}{\:\sqrt{\left(\Delta{x}\right)^{\mathrm{2}} +\left(\Delta{y}\right)^{\mathrm{2}} }}=\frac{\Delta{z}}{\:\sqrt{\left(\Delta{l}\right)^{\mathrm{2}} −\left(\Delta{z}\right)^{\mathrm{2}} }} \\ $$$${with}\:\Delta{l}=\sqrt{\left(\Delta{x}\right)^{\mathrm{2}} +\left(\Delta{y}\right)^{\mathrm{2}} +\left(\Delta{z}\right)^{\mathrm{2}} } \\ $$

Commented by mr W last updated on 18/Feb/21

$${could}\:{you}\:{go}\:{with}\:{this}\:{definition}\:{sir}? \\ $$

Answered by mr W last updated on 18/Feb/21

Commented by mr W last updated on 17/Feb/21

P=peak of mountain let λ=(r/h) γ=tan^(−1) (r/h)=tan^(−1) λ s_A =PA s_B =PB s_A =(√(h^2 +r^2 ))=h (√(1+λ^2 )) (s_B /(sin ((π/2)−θ)))=(h/(sin ((π/2)−θ+γ))) s_B =((cos θ h)/(cos (θ−γ)))=(h/(cos γ+sin γ tan θ)) s_B =((h(√(1+λ^2 )))/(1+λtan θ)) when the surface of the cone is unfolded, the shortest road from A to B is the straight line AB. AA^(⌢) ′=2πr ϕ=((2πr)/s_A )=((2πr)/( (√(h^2 +r^2 ))))=((2πλ)/( (√(1+λ^2 )))) (assume ϕ<π, i.e. λ<(1/( (√3))) or γ<30°) length of road =L_I L_I =AB=(√(s_A ^2 +s_B ^2 −2s_A s_B cos ϕ)) L_I =(√(h^2 +r^2 +((h^2 (1+λ^2 ))/((1+λtan θ)^2 ))−((2h(√((1+λ^2 )(h^2 +r^2 ))))/(1+λtan θ)) cos ((2πλ)/( (√(1+λ^2 )))))) (L_I /h)=(√((1+λ^2 )[1+(1/((1+λtan θ)^2 ))−(2/(1+λtan θ)) cos ((2πλ)/( (√(1+λ^2 ))))])) example: λ=(1/3), θ=45° (L_I /h)=(5/(12))(√(10(1−((24)/(25)) cos (((√(10))π)/( 5)))))≈1.552354 we see by road I, the point B is not always the highest point on the road. the highest point on the road has the closest distance to the peak P, this is the point M. ((sin (ϕ+α))/(sin α))=(s_A /s_B ) ((sin ϕ)/(tan α))+cos ϕ=1+λtan θ tan α=((sin ϕ)/(1+λtan θ−cos ϕ)) s_M =PM=s_A sin α ⇒s_M =((h(√(1+λ^2 )) sin ϕ)/( (√(1+(1+λtan θ)(1+λtan θ−2cos ϕ)))))

$${P}={peak}\:{of}\:{mountain} \\ $$$${let}\:\lambda=\frac{{r}}{{h}} \\ $$$$\gamma=\mathrm{tan}^{−\mathrm{1}} \frac{{r}}{{h}}=\mathrm{tan}^{−\mathrm{1}} \lambda \\ $$$${s}_{{A}} ={PA} \\ $$$${s}_{{B}} ={PB} \\ $$$${s}_{{A}} =\sqrt{{h}^{\mathrm{2}} +{r}^{\mathrm{2}} }={h}\:\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} } \\ $$$$\frac{{s}_{{B}} }{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\theta\right)}=\frac{{h}}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\theta+\gamma\right)} \\ $$$${s}_{{B}} =\frac{\mathrm{cos}\:\theta\:{h}}{\mathrm{cos}\:\left(\theta−\gamma\right)}=\frac{{h}}{\mathrm{cos}\:\gamma+\mathrm{sin}\:\gamma\:\mathrm{tan}\:\theta} \\ $$$${s}_{{B}} =\frac{{h}\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }}{\mathrm{1}+\lambda\mathrm{tan}\:\theta} \\ $$$$ \\ $$$${when}\:{the}\:{surface}\:{of}\:{the}\:{cone}\:{is} \\ $$$${unfolded},\:{the}\:{shortest}\:{road}\:{from} \\ $$$${A}\:{to}\:{B}\:{is}\:{the}\:{straight}\:{line}\:{AB}. \\ $$$$\overset{\frown} {{AA}}'=\mathrm{2}\pi{r} \\ $$$$\varphi=\frac{\mathrm{2}\pi{r}}{{s}_{{A}} }=\frac{\mathrm{2}\pi{r}}{\:\sqrt{{h}^{\mathrm{2}} +{r}^{\mathrm{2}} }}=\frac{\mathrm{2}\pi\lambda}{\:\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }} \\ $$$$\left({assume}\:\varphi<\pi,\:{i}.{e}.\:\lambda<\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:{or}\:\gamma<\mathrm{30}°\right) \\ $$$$ \\ $$$${length}\:{of}\:{road}\:={L}_{{I}} \\ $$$${L}_{{I}} ={AB}=\sqrt{{s}_{{A}} ^{\mathrm{2}} +{s}_{{B}} ^{\mathrm{2}} −\mathrm{2}{s}_{{A}} {s}_{{B}} \mathrm{cos}\:\varphi} \\ $$$${L}_{{I}} =\sqrt{{h}^{\mathrm{2}} +{r}^{\mathrm{2}} +\frac{{h}^{\mathrm{2}} \left(\mathrm{1}+\lambda^{\mathrm{2}} \right)}{\left(\mathrm{1}+\lambda\mathrm{tan}\:\theta\right)^{\mathrm{2}} }−\frac{\mathrm{2}{h}\sqrt{\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)\left({h}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)}}{\mathrm{1}+\lambda\mathrm{tan}\:\theta}\:\mathrm{cos}\:\frac{\mathrm{2}\pi\lambda}{\:\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }}} \\ $$$$\frac{{L}_{{I}} }{{h}}=\sqrt{\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)\left[\mathrm{1}+\frac{\mathrm{1}}{\left(\mathrm{1}+\lambda\mathrm{tan}\:\theta\right)^{\mathrm{2}} }−\frac{\mathrm{2}}{\mathrm{1}+\lambda\mathrm{tan}\:\theta}\:\mathrm{cos}\:\frac{\mathrm{2}\pi\lambda}{\:\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }}\right]} \\ $$$$ \\ $$$${example}: \\ $$$$\lambda=\frac{\mathrm{1}}{\mathrm{3}},\:\theta=\mathrm{45}° \\ $$$$\frac{{L}_{{I}} }{{h}}=\frac{\mathrm{5}}{\mathrm{12}}\sqrt{\mathrm{10}\left(\mathrm{1}−\frac{\mathrm{24}}{\mathrm{25}}\:\mathrm{cos}\:\frac{\sqrt{\mathrm{10}}\pi}{\:\mathrm{5}}\right)}\approx\mathrm{1}.\mathrm{552354} \\ $$$$ \\ $$$${we}\:{see}\:{by}\:{road}\:{I},\:{the}\:{point}\:{B}\:{is}\:{not} \\ $$$${always}\:{the}\:{highest}\:{point}\:{on}\:{the}\:{road}. \\ $$$${the}\:{highest}\:{point}\:{on}\:{the}\:{road}\:{has}\:{the} \\ $$$${closest}\:{distance}\:{to}\:{the}\:{peak}\:{P},\:{this} \\ $$$${is}\:{the}\:{point}\:{M}. \\ $$$$\frac{\mathrm{sin}\:\left(\varphi+\alpha\right)}{\mathrm{sin}\:\alpha}=\frac{{s}_{{A}} }{{s}_{{B}} } \\ $$$$\frac{\mathrm{sin}\:\varphi}{\mathrm{tan}\:\alpha}+\mathrm{cos}\:\varphi=\mathrm{1}+\lambda\mathrm{tan}\:\theta \\ $$$$\mathrm{tan}\:\alpha=\frac{\mathrm{sin}\:\varphi}{\mathrm{1}+\lambda\mathrm{tan}\:\theta−\mathrm{cos}\:\varphi} \\ $$$${s}_{{M}} ={PM}={s}_{{A}} \:\mathrm{sin}\:\alpha \\ $$$$\Rightarrow{s}_{{M}} =\frac{{h}\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }\:\mathrm{sin}\:\varphi}{\:\sqrt{\mathrm{1}+\left(\mathrm{1}+\lambda\mathrm{tan}\:\theta\right)\left(\mathrm{1}+\lambda\mathrm{tan}\:\theta−\mathrm{2cos}\:\varphi\right)}} \\ $$

Commented by MJS_new last updated on 17/Feb/21

just saying, the shortest distance is straight up the mountain and it′s also a route with constant slope ;−)

$$\mathrm{just}\:\mathrm{saying},\:\mathrm{the}\:\mathrm{shortest}\:\mathrm{distance}\:\mathrm{is}\:\mathrm{straight} \\ $$$$\mathrm{up}\:\mathrm{the}\:\mathrm{mountain}\:\mathrm{and}\:\mathrm{it}'\mathrm{s}\:\mathrm{also}\:\mathrm{a}\:\mathrm{route}\:\mathrm{with} \\ $$$$\left.\mathrm{constant}\:\mathrm{slope}\:;−\right) \\ $$

Commented by mr W last updated on 17/Feb/21

$${the}\:{roads}\:{should}\:{be}\:{around}\:{the} \\ $$$${mountain},\:{therefore}\:{the}\:{direct}\:{way} \\ $$$${right}\:{up}\:{from}\:{A}\:{to}\:{B}\:{is}\:{not}\:{valid}\::\left(\right. \\ $$

Commented by mr W last updated on 17/Feb/21

Commented by mr W last updated on 19/Feb/21

λ=(r/h) s_A =(√(h^2 +r^2 ))=h (√(1+λ^2 )) s_B =((h(√(1+λ^2 )))/(1+λtan θ)) ϕ=((2πλ)/( (√(1+λ^2 )))) α=tan^(−1) ((sin ϕ)/(1+λtan θ−cos ϕ)) s=PC (s/(sin α))=(s_A /(sin (α+δ))) ⇒s=((h(√(1+λ^2 )))/(cos δ+((sin δ)/(tan α)))) (ds/dδ)=((s(sin δ−((cos δ)/(tan α))))/(cos δ+((sin δ)/(tan α))))=−(s/(tan (α+δ))) φr=δs_A ⇒φ=((δ(√(1+λ^2 )))/λ) z=h−s cos γ=h−(s/( (√(1+λ^2 )))) ρ=s sin γ=((λs)/( (√(1+λ^2 )))) slope k=(dz/( (√((dρ)^2 +(ρdφ)^2 )))) k=((−(dz/ds))/( (√(((dρ/ds))^2 +(((ρ×(dφ/dδ))/(ds/dδ)))^2 )))) k=((1/( (√(1+λ^2 ))))/( (√(((λ/( (√(1+λ^2 )))))^2 +(((((λs)/( (√(1+λ^2 ))))×((√(1+λ^2 ))/λ))/(−(s/(tan (α+δ))))))^2 )))) ⇒k=(1/( (√(λ^2 +(1+λ^2 )tan^2 (α+δ))))) we see the maximum slope is at δ=0, i.e. at point A, or at δ=ϕ, i.e. at point B. k_A =(1/( (√(λ^2 +(1+λ^2 )tan^2 (α))))) (uphill) k_B =(1/( (√(λ^2 +(1+λ^2 )tan^2 (α+ϕ))))) (downhill) the smallest slope is zero when δ+α=(π/2) this is at the point M, the highest pioint on the road. example: λ=(1/3), θ=45° ϕ=((2πλ)/( (√(1+λ^2 ))))=((2π)/( (√(10)))) tan α=((sin ϕ)/(1+λtan θ−cos ϕ))=((sin ((2π)/( (√(10)))))/((4/3)−cos ((2π)/( (√(10)))))) k_(max) =(3/( (√(1+10(((sin ((2π)/( (√(10)))))/((4/3)−cos ((2π)/( (√(10)))))))^2 ))))=1.544 858

$$\lambda=\frac{{r}}{{h}} \\ $$$${s}_{{A}} =\sqrt{{h}^{\mathrm{2}} +{r}^{\mathrm{2}} }={h}\:\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} } \\ $$$${s}_{{B}} =\frac{{h}\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }}{\mathrm{1}+\lambda\mathrm{tan}\:\theta} \\ $$$$\varphi=\frac{\mathrm{2}\pi\lambda}{\:\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }} \\ $$$$\alpha=\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{sin}\:\varphi}{\mathrm{1}+\lambda\mathrm{tan}\:\theta−\mathrm{cos}\:\varphi} \\ $$$${s}={PC} \\ $$$$\frac{{s}}{\mathrm{sin}\:\alpha}=\frac{{s}_{{A}} }{\mathrm{sin}\:\left(\alpha+\delta\right)} \\ $$$$\Rightarrow{s}=\frac{{h}\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }}{\mathrm{cos}\:\delta+\frac{\mathrm{sin}\:\delta}{\mathrm{tan}\:\alpha}} \\ $$$$\frac{{ds}}{{d}\delta}=\frac{{s}\left(\mathrm{sin}\:\delta−\frac{\mathrm{cos}\:\delta}{\mathrm{tan}\:\alpha}\right)}{\mathrm{cos}\:\delta+\frac{\mathrm{sin}\:\delta}{\mathrm{tan}\:\alpha}}=−\frac{{s}}{\mathrm{tan}\:\left(\alpha+\delta\right)} \\ $$$$\phi{r}=\delta{s}_{{A}} \\ $$$$\Rightarrow\phi=\frac{\delta\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }}{\lambda} \\ $$$${z}={h}−{s}\:\mathrm{cos}\:\gamma={h}−\frac{{s}}{\:\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }} \\ $$$$\rho={s}\:\mathrm{sin}\:\gamma=\frac{\lambda{s}}{\:\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }} \\ $$$${slope}\:{k}=\frac{{dz}}{\:\sqrt{\left({d}\rho\right)^{\mathrm{2}} +\left(\rho{d}\phi\right)^{\mathrm{2}} }} \\ $$$${k}=\frac{−\frac{{dz}}{{ds}}}{\:\sqrt{\left(\frac{{d}\rho}{{ds}}\right)^{\mathrm{2}} +\left(\frac{\rho×\frac{{d}\phi}{{d}\delta}}{\frac{{ds}}{{d}\delta}}\right)^{\mathrm{2}} }} \\ $$$${k}=\frac{\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }}}{\:\sqrt{\left(\frac{\lambda}{\:\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }}\right)^{\mathrm{2}} +\left(\frac{\frac{\lambda{s}}{\:\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }}×\frac{\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }}{\lambda}}{−\frac{{s}}{\mathrm{tan}\:\left(\alpha+\delta\right)}}\right)^{\mathrm{2}} }} \\ $$$$\Rightarrow{k}=\frac{\mathrm{1}}{\:\sqrt{\lambda^{\mathrm{2}} +\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)\mathrm{tan}^{\mathrm{2}} \:\left(\alpha+\delta\right)}} \\ $$$$ \\ $$$${we}\:{see}\:{the}\:{maximum}\:{slope}\:{is}\:{at} \\ $$$$\delta=\mathrm{0},\:{i}.{e}.\:{at}\:{point}\:{A},\:{or}\:{at}\:\delta=\varphi,\:{i}.{e}. \\ $$$${at}\:{point}\:{B}. \\ $$$${k}_{{A}} =\frac{\mathrm{1}}{\:\sqrt{\lambda^{\mathrm{2}} +\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)\mathrm{tan}^{\mathrm{2}} \:\left(\alpha\right)}}\:\left({uphill}\right) \\ $$$${k}_{{B}} =\frac{\mathrm{1}}{\:\sqrt{\lambda^{\mathrm{2}} +\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)\mathrm{tan}^{\mathrm{2}} \:\left(\alpha+\varphi\right)}}\:\left({downhill}\right) \\ $$$$ \\ $$$${the}\:{smallest}\:{slope}\:{is}\:{zero}\:{when} \\ $$$$\delta+\alpha=\frac{\pi}{\mathrm{2}} \\ $$$${this}\:{is}\:{at}\:{the}\:{point}\:{M},\:{the}\:{highest} \\ $$$${pioint}\:{on}\:{the}\:{road}. \\ $$$$ \\ $$$${example}: \\ $$$$\lambda=\frac{\mathrm{1}}{\mathrm{3}},\:\theta=\mathrm{45}° \\ $$$$\varphi=\frac{\mathrm{2}\pi\lambda}{\:\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }}=\frac{\mathrm{2}\pi}{\:\sqrt{\mathrm{10}}} \\ $$$$\mathrm{tan}\:\alpha=\frac{\mathrm{sin}\:\varphi}{\mathrm{1}+\lambda\mathrm{tan}\:\theta−\mathrm{cos}\:\varphi}=\frac{\mathrm{sin}\:\frac{\mathrm{2}\pi}{\:\sqrt{\mathrm{10}}}}{\frac{\mathrm{4}}{\mathrm{3}}−\mathrm{cos}\:\frac{\mathrm{2}\pi}{\:\sqrt{\mathrm{10}}}} \\ $$$${k}_{{max}} =\frac{\mathrm{3}}{\:\sqrt{\mathrm{1}+\mathrm{10}\left(\frac{\mathrm{sin}\:\frac{\mathrm{2}\pi}{\:\sqrt{\mathrm{10}}}}{\frac{\mathrm{4}}{\mathrm{3}}−\mathrm{cos}\:\frac{\mathrm{2}\pi}{\:\sqrt{\mathrm{10}}}}\right)^{\mathrm{2}} }}=\mathrm{1}.\mathrm{544}\:\mathrm{858} \\ $$

Commented by MJS_new last updated on 17/Feb/21

the concept of the shortest distance around the cone is fuzzy... (1) if B=P it′s no more “around the cone” (2) if ϕ=180° it′s straight up over the peak (3) if ϕ>180° where is it? (4) let B=A in cases (2) and (3) this isn′t criticism, I′m just playing around with it if B is not 360° away from A it works better because we could go the other direction...

$$\mathrm{the}\:\mathrm{concept}\:\mathrm{of}\:\mathrm{the}\:\mathrm{shortest}\:\mathrm{distance}\:\mathrm{around} \\ $$$$\mathrm{the}\:\mathrm{cone}\:\mathrm{is}\:\mathrm{fuzzy}… \\ $$$$\left(\mathrm{1}\right)\:\mathrm{if}\:{B}={P}\:\mathrm{it}'\mathrm{s}\:\mathrm{no}\:\mathrm{more}\:“\mathrm{around}\:\mathrm{the}\:\mathrm{cone}'' \\ $$$$\left(\mathrm{2}\right)\:\mathrm{if}\:\varphi=\mathrm{180}°\:\mathrm{it}'\mathrm{s}\:\mathrm{straight}\:\mathrm{up}\:\mathrm{over}\:\mathrm{the}\:\mathrm{peak} \\ $$$$\left(\mathrm{3}\right)\:\mathrm{if}\:\varphi>\mathrm{180}°\:\mathrm{where}\:\mathrm{is}\:\mathrm{it}? \\ $$$$\left(\mathrm{4}\right)\:\mathrm{let}\:{B}={A}\:\mathrm{in}\:\mathrm{cases}\:\left(\mathrm{2}\right)\:\mathrm{and}\:\left(\mathrm{3}\right) \\ $$$$\mathrm{this}\:\mathrm{isn}'\mathrm{t}\:\mathrm{criticism},\:\mathrm{I}'\mathrm{m}\:\mathrm{just}\:\mathrm{playing}\:\mathrm{around} \\ $$$$\mathrm{with}\:\mathrm{it} \\ $$$$\mathrm{if}\:{B}\:\mathrm{is}\:\mathrm{not}\:\mathrm{360}°\:\mathrm{away}\:\mathrm{from}\:{A}\:\mathrm{it}\:\mathrm{works}\:\mathrm{better} \\ $$$$\mathrm{because}\:\mathrm{we}\:\mathrm{could}\:\mathrm{go}\:\mathrm{the}\:\mathrm{other}\:\mathrm{direction}… \\ $$

Commented by mr W last updated on 18/Feb/21

i have added a restriction: h>(√3)r. actually i′m also playing with it, so all are allowed to play in their ways, and you in your way.

$${i}\:{have}\:{added}\:{a}\:{restriction}:\:{h}>\sqrt{\mathrm{3}}{r}. \\ $$$${actually}\:{i}'{m}\:{also}\:{playing}\:{with}\:{it},\:{so} \\ $$$${all}\:{are}\:{allowed}\:{to}\:{play}\:{in}\:{their}\:{ways}, \\ $$$${and}\:{you}\:{in}\:{your}\:{way}. \\ $$

Answered by mr W last updated on 18/Feb/21

Commented by mr W last updated on 18/Feb/21

Commented by mr W last updated on 19/Feb/21

we have got from road I: tan γ=(r/h)=λ s_A =h (√(1+λ^2 )) s_B =((h(√(1+λ^2 )))/(1+λtan θ)) ϕ=((2πλ)/( (√(1+λ^2 )))) s=PC φr=δs_A φ=((δ(√(1+λ^2 )))/λ) z=C′C=h−s cos γ=h−(s/( (√(1+λ^2 )))) ρ=OC′=s sin γ=((λs)/( (√(1+λ^2 )))) slope k=(dz/( (√((dρ)^2 +(ρdφ)^2 )))) k=((−(dz/ds))/( (√(((dρ/ds))^2 +(((ρ×(dφ/dδ))/(ds/dδ)))^2 )))) k=((1/( (√(1+λ^2 ))))/( (√(((λ/( (√(1+λ^2 )))))^2 +(((((λs)/( (√(1+λ^2 ))))×((√(1+λ^2 ))/λ))/(ds/dδ)))^2 )))) k=(1/( (√(λ^2 +(1+λ^2 )((s/(ds/dδ)))^2 )))) (ds/dδ)=−(s/( (√((1/(1+λ^2 ))((1/( k^2 ))−λ^2 ))))) let ξ=(1/( (√((1/(1+λ^2 ))((1/( k^2 ))−λ^2 ))))) ∫_s_A ^s (ds/s)=−ξ∫_0 ^δ dδ ln s−ln s_A =−ξδ s=s_A e^(−ξδ) ⇒s=h(√(1+λ^2 ))e^(−ξδ) s_B =h(√(1+λ^2 ))e^(−ξϕ) =((h(√(1+λ^2 )))/(1+λtan θ)) e^(−ξϕ) =(1/(1+λtan θ)) ξ=((ln (1+λtan θ))/ϕ) (1/( (√((1/(1+λ^2 ))((1/( k^2 ))−λ^2 )))))=((ln (1+λtan θ))/ϕ) (1/( (1/( k^2 ))−λ^2 ))=((ln^2 (1+λtan θ))/((1+λ^2 )ϕ^2 )) (1/k^2 )=λ^2 +(((1+λ^2 )ϕ^2 )/( ln^2 (1+λtan θ)))=λ^2 +((4π^2 λ^2 )/( ln^2 (1+λtan θ))) ⇒k=(1/( λ(√(1+[((2π)/( ln (1+λtan θ)))]^2 )))) length of road L_(II) L_(II) =∫_0 ^ϕ (√(s^2 +((ds/dδ))^2 ))dδ L_(II) =h(√(1+λ^2 ))∫_0 ^ϕ e^(−ξδ) (√(1+ξ^2 ))dδ (L_(II) /h)=(((1−e^(−ξϕ) )(√((1+λ^2 )(1+ξ^2 ))))/ξ) ⇒(L_(II) /h)=(1−(1/(1+λtan θ)))(√(1+λ^2 +[((2πλ)/(ln (1+λtan θ)))]^2 )) or L_(II) =((√(1+k^2 ))/k)(s_A −s_B )cos γ L_(II) =h(√(1+(1/k^2 )))(1−(1/(1+λtan θ))) ⇒(L_(II) /h)=(1−(1/(1+λtan θ)))(√(1+λ^2 +[((2πλ)/( ln (1+λtan θ)))]^2 )) example: λ=(1/3), θ=45° (L_(II) /h)=(1/(12))(√(10+(((2π)/( ln (4/3))))^2 ))≈1.839 039 058 k=(3/( (√(1+(((2π)/( ln (4/3))))^2 ))))=0.137 214

$${we}\:{have}\:{got}\:{from}\:{road}\:{I}: \\ $$$$\mathrm{tan}\:\gamma=\frac{{r}}{{h}}=\lambda \\ $$$${s}_{{A}} ={h}\:\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} } \\ $$$${s}_{{B}} =\frac{{h}\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }}{\mathrm{1}+\lambda\mathrm{tan}\:\theta} \\ $$$$\varphi=\frac{\mathrm{2}\pi\lambda}{\:\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }} \\ $$$${s}={PC} \\ $$$$\phi{r}=\delta{s}_{{A}} \\ $$$$\phi=\frac{\delta\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }}{\lambda} \\ $$$${z}={C}'{C}={h}−{s}\:\mathrm{cos}\:\gamma={h}−\frac{{s}}{\:\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }} \\ $$$$\rho={OC}'={s}\:\mathrm{sin}\:\gamma=\frac{\lambda{s}}{\:\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }} \\ $$$${slope}\:{k}=\frac{{dz}}{\:\sqrt{\left({d}\rho\right)^{\mathrm{2}} +\left(\rho{d}\phi\right)^{\mathrm{2}} }} \\ $$$${k}=\frac{−\frac{{dz}}{{ds}}}{\:\sqrt{\left(\frac{{d}\rho}{{ds}}\right)^{\mathrm{2}} +\left(\frac{\rho×\frac{{d}\phi}{{d}\delta}}{\frac{{ds}}{{d}\delta}}\right)^{\mathrm{2}} }} \\ $$$${k}=\frac{\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }}}{\:\sqrt{\left(\frac{\lambda}{\:\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }}\right)^{\mathrm{2}} +\left(\frac{\frac{\lambda{s}}{\:\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }}×\frac{\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }}{\lambda}}{\frac{{ds}}{{d}\delta}}\right)^{\mathrm{2}} }} \\ $$$${k}=\frac{\mathrm{1}}{\:\sqrt{\lambda^{\mathrm{2}} +\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)\left(\frac{{s}}{\frac{{ds}}{{d}\delta}}\right)^{\mathrm{2}} }} \\ $$$$\frac{{ds}}{{d}\delta}=−\frac{{s}}{\:\sqrt{\frac{\mathrm{1}}{\mathrm{1}+\lambda^{\mathrm{2}} }\left(\frac{\mathrm{1}}{\:{k}^{\mathrm{2}} }−\lambda^{\mathrm{2}} \right)}} \\ $$$${let}\:\xi=\frac{\mathrm{1}}{\:\sqrt{\frac{\mathrm{1}}{\mathrm{1}+\lambda^{\mathrm{2}} }\left(\frac{\mathrm{1}}{\:{k}^{\mathrm{2}} }−\lambda^{\mathrm{2}} \right)}} \\ $$$$\int_{{s}_{{A}} } ^{{s}} \frac{{ds}}{{s}}=−\xi\int_{\mathrm{0}} ^{\delta} {d}\delta \\ $$$$\mathrm{ln}\:{s}−\mathrm{ln}\:{s}_{{A}} =−\xi\delta \\ $$$${s}={s}_{{A}} {e}^{−\xi\delta} \\ $$$$\Rightarrow{s}={h}\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }{e}^{−\xi\delta} \\ $$$${s}_{{B}} ={h}\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }{e}^{−\xi\varphi} =\frac{{h}\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }}{\mathrm{1}+\lambda\mathrm{tan}\:\theta} \\ $$$${e}^{−\xi\varphi} =\frac{\mathrm{1}}{\mathrm{1}+\lambda\mathrm{tan}\:\theta} \\ $$$$\xi=\frac{\mathrm{ln}\:\left(\mathrm{1}+\lambda\mathrm{tan}\:\theta\right)}{\varphi} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\frac{\mathrm{1}}{\mathrm{1}+\lambda^{\mathrm{2}} }\left(\frac{\mathrm{1}}{\:{k}^{\mathrm{2}} }−\lambda^{\mathrm{2}} \right)}}=\frac{\mathrm{ln}\:\left(\mathrm{1}+\lambda\mathrm{tan}\:\theta\right)}{\varphi} \\ $$$$\frac{\mathrm{1}}{\:\frac{\mathrm{1}}{\:{k}^{\mathrm{2}} }−\lambda^{\mathrm{2}} }=\frac{\mathrm{ln}^{\mathrm{2}} \:\left(\mathrm{1}+\lambda\mathrm{tan}\:\theta\right)}{\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)\varphi^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{{k}^{\mathrm{2}} }=\lambda^{\mathrm{2}} +\frac{\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)\varphi^{\mathrm{2}} }{\:\mathrm{ln}^{\mathrm{2}} \:\left(\mathrm{1}+\lambda\mathrm{tan}\:\theta\right)}=\lambda^{\mathrm{2}} +\frac{\mathrm{4}\pi^{\mathrm{2}} \lambda^{\mathrm{2}} }{\:\mathrm{ln}^{\mathrm{2}} \:\left(\mathrm{1}+\lambda\mathrm{tan}\:\theta\right)} \\ $$$$\Rightarrow{k}=\frac{\mathrm{1}}{\:\lambda\sqrt{\mathrm{1}+\left[\frac{\mathrm{2}\pi}{\:\mathrm{ln}\:\left(\mathrm{1}+\lambda\mathrm{tan}\:\theta\right)}\right]^{\mathrm{2}} }} \\ $$$$ \\ $$$${length}\:{of}\:{road}\:{L}_{{II}} \\ $$$${L}_{{II}} =\int_{\mathrm{0}} ^{\varphi} \sqrt{{s}^{\mathrm{2}} +\left(\frac{{ds}}{{d}\delta}\right)^{\mathrm{2}} }{d}\delta \\ $$$${L}_{{II}} ={h}\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }\int_{\mathrm{0}} ^{\varphi} {e}^{−\xi\delta} \sqrt{\mathrm{1}+\xi^{\mathrm{2}} }{d}\delta \\ $$$$\frac{{L}_{{II}} }{{h}}=\frac{\left(\mathrm{1}−{e}^{−\xi\varphi} \right)\sqrt{\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)\left(\mathrm{1}+\xi^{\mathrm{2}} \right)}}{\xi} \\ $$$$\Rightarrow\frac{{L}_{{II}} }{{h}}=\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+\lambda\mathrm{tan}\:\theta}\right)\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} +\left[\frac{\mathrm{2}\pi\lambda}{\mathrm{ln}\:\left(\mathrm{1}+\lambda\mathrm{tan}\:\theta\right)}\right]^{\mathrm{2}} } \\ $$$${or} \\ $$$${L}_{{II}} =\frac{\sqrt{\mathrm{1}+{k}^{\mathrm{2}} }}{{k}}\left({s}_{{A}} −{s}_{{B}} \right)\mathrm{cos}\:\gamma \\ $$$${L}_{{II}} ={h}\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{k}^{\mathrm{2}} }}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+\lambda\mathrm{tan}\:\theta}\right) \\ $$$$\Rightarrow\frac{{L}_{{II}} }{{h}}=\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+\lambda\mathrm{tan}\:\theta}\right)\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} +\left[\frac{\mathrm{2}\pi\lambda}{\:\mathrm{ln}\:\left(\mathrm{1}+\lambda\mathrm{tan}\:\theta\right)}\right]^{\mathrm{2}} } \\ $$$$ \\ $$$${example}: \\ $$$$\lambda=\frac{\mathrm{1}}{\mathrm{3}},\:\theta=\mathrm{45}° \\ $$$$\frac{{L}_{{II}} }{{h}}=\frac{\mathrm{1}}{\mathrm{12}}\sqrt{\mathrm{10}+\left(\frac{\mathrm{2}\pi}{\:\mathrm{ln}\:\frac{\mathrm{4}}{\mathrm{3}}}\right)^{\mathrm{2}} }\approx\mathrm{1}.\mathrm{839}\:\mathrm{039}\:\mathrm{058} \\ $$$${k}=\frac{\mathrm{3}}{\:\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}\pi}{\:\mathrm{ln}\:\frac{\mathrm{4}}{\mathrm{3}}}\right)^{\mathrm{2}} }}=\mathrm{0}.\mathrm{137}\:\mathrm{214} \\ $$

Commented by mr W last updated on 18/Feb/21