Question Number 132905 by bramlexs22 last updated on 17/Feb/21

Answered by bobhans last updated on 17/Feb/21
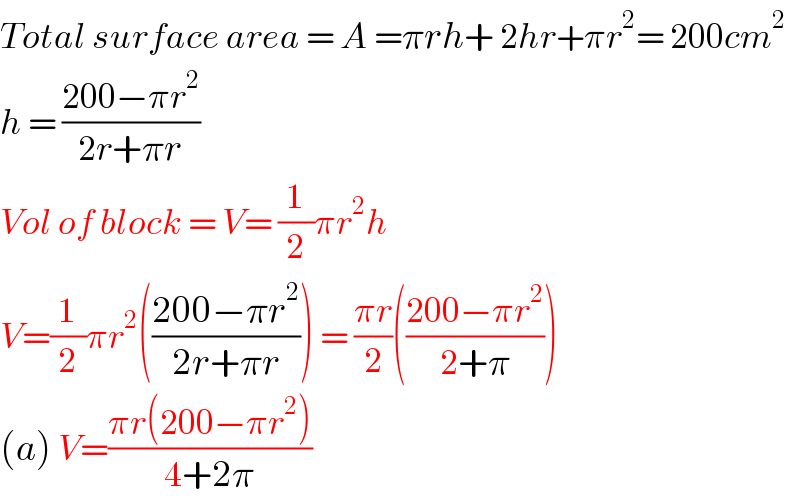
$${Total}\:{surface}\:{area}\:=\:{A}\:=\pi{rh}+\:\mathrm{2}{hr}+\pi{r}^{\mathrm{2}} =\:\mathrm{200}{cm}^{\mathrm{2}} \\ $$$${h}\:=\:\frac{\mathrm{200}−\pi{r}^{\mathrm{2}} }{\mathrm{2}{r}+\pi{r}} \\ $$$${Vol}\:{of}\:{block}\:=\:{V}=\:\frac{\mathrm{1}}{\mathrm{2}}\pi{r}^{\mathrm{2}} {h} \\ $$$${V}=\frac{\mathrm{1}}{\mathrm{2}}\pi{r}^{\mathrm{2}} \left(\frac{\mathrm{200}−\pi{r}^{\mathrm{2}} }{\mathrm{2}{r}+\pi{r}}\right)\:=\:\frac{\pi{r}}{\mathrm{2}}\left(\frac{\mathrm{200}−\pi{r}^{\mathrm{2}} }{\mathrm{2}+\pi}\right) \\ $$$$\left({a}\right)\:{V}=\frac{\pi{r}\left(\mathrm{200}−\pi{r}^{\mathrm{2}} \right)}{\mathrm{4}+\mathrm{2}\pi} \\ $$
Answered by bobhans last updated on 17/Feb/21
![(b)maximum value of V. (dV/dr) = (1/(2π+4)) (d/dr)[ 200πr − π^2 r^3 ] = 0 ⇔ (1/(2π+4)) [ 200π−3π^2 r^2 ] = 0 ⇒ r =(√((200)/(3π))) V_(max) = ((π((√((200)/(3π))))(200−π(((200)/(3π)))))/(2π+4)) V_(max) = ((4000π(√2))/((2π+4)(√(3π)))) = ((2000(√(2π)))/((π+2)(√3))) cm^3](https://www.tinkutara.com/question/Q132907.png)
$$\left({b}\right){maximum}\:{value}\:{of}\:{V}. \\ $$$$\:\frac{{dV}}{{dr}}\:=\:\frac{\mathrm{1}}{\mathrm{2}\pi+\mathrm{4}}\:\frac{{d}}{{dr}}\left[\:\mathrm{200}\pi{r}\:−\:\pi^{\mathrm{2}} {r}^{\mathrm{3}} \:\right]\:=\:\mathrm{0}\: \\ $$$$\:\Leftrightarrow\:\frac{\mathrm{1}}{\mathrm{2}\pi+\mathrm{4}}\:\left[\:\mathrm{200}\pi−\mathrm{3}\pi^{\mathrm{2}} {r}^{\mathrm{2}} \:\right]\:=\:\mathrm{0} \\ $$$$\Rightarrow\:{r}\:=\sqrt{\frac{\mathrm{200}}{\mathrm{3}\pi}}\: \\ $$$${V}_{{max}} \:=\:\frac{\pi\left(\sqrt{\frac{\mathrm{200}}{\mathrm{3}\pi}}\right)\left(\mathrm{200}−\pi\left(\frac{\mathrm{200}}{\mathrm{3}\pi}\right)\right)}{\mathrm{2}\pi+\mathrm{4}} \\ $$$${V}_{{max}} \:=\:\frac{\mathrm{4000}\pi\sqrt{\mathrm{2}}}{\left(\mathrm{2}\pi+\mathrm{4}\right)\sqrt{\mathrm{3}\pi}}\:=\:\frac{\mathrm{2000}\sqrt{\mathrm{2}\pi}}{\left(\pi+\mathrm{2}\right)\sqrt{\mathrm{3}}}\:{cm}^{\mathrm{3}} \\ $$
Commented by bramlexs22 last updated on 17/Feb/21

$$\mathrm{thanks} \\ $$
