Question Number 133168 by bemath last updated on 19/Feb/21
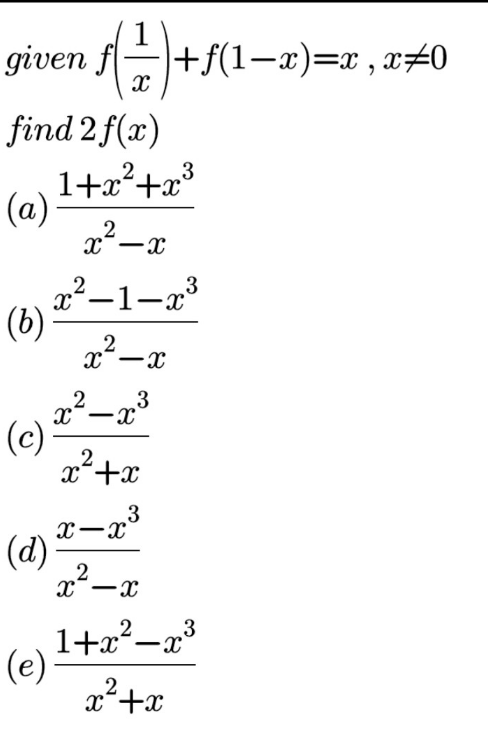
Answered by floor(10²Eta[1]) last updated on 19/Feb/21
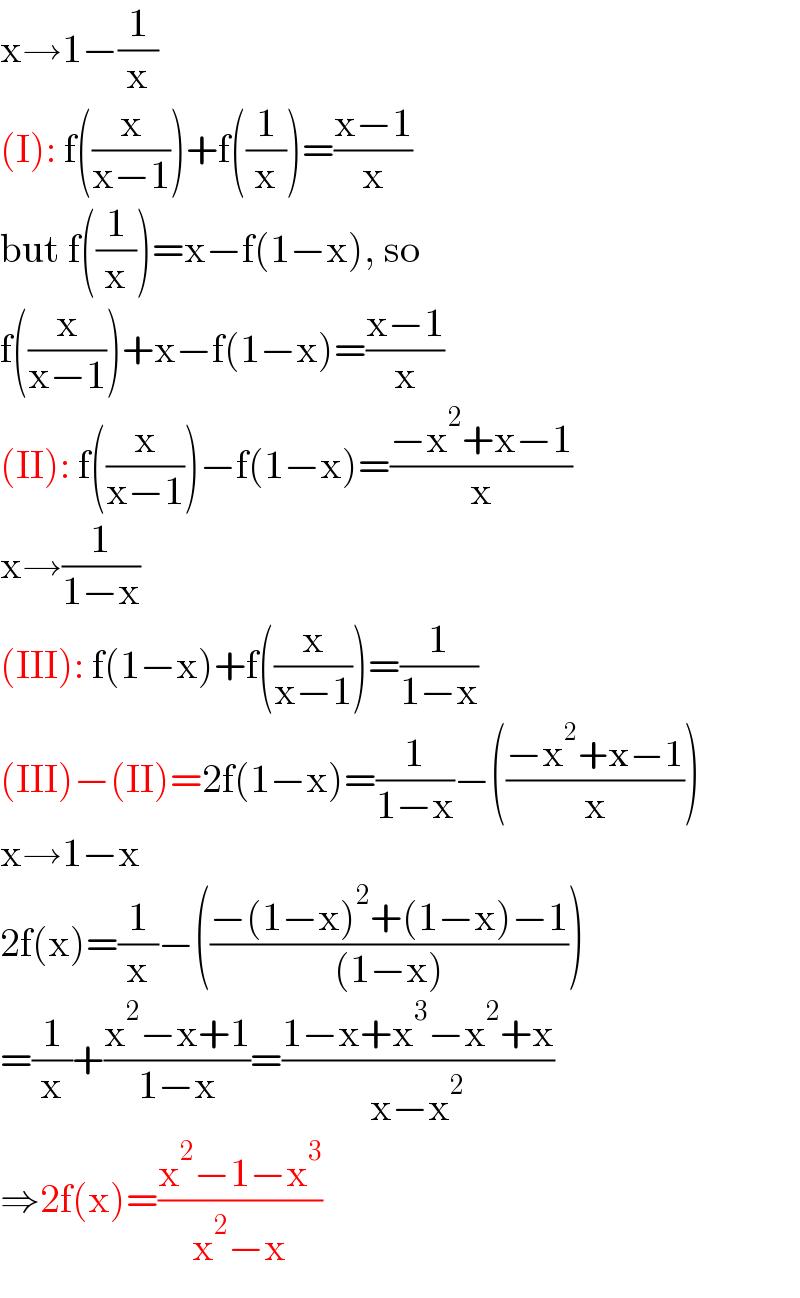
$$\mathrm{x}\rightarrow\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}} \\ $$$$\left(\mathrm{I}\right):\:\mathrm{f}\left(\frac{\mathrm{x}}{\mathrm{x}−\mathrm{1}}\right)+\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)=\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}} \\ $$$$\mathrm{but}\:\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)=\mathrm{x}−\mathrm{f}\left(\mathrm{1}−\mathrm{x}\right),\:\mathrm{so} \\ $$$$\mathrm{f}\left(\frac{\mathrm{x}}{\mathrm{x}−\mathrm{1}}\right)+\mathrm{x}−\mathrm{f}\left(\mathrm{1}−\mathrm{x}\right)=\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}} \\ $$$$\left(\mathrm{II}\right):\:\mathrm{f}\left(\frac{\mathrm{x}}{\mathrm{x}−\mathrm{1}}\right)−\mathrm{f}\left(\mathrm{1}−\mathrm{x}\right)=\frac{−\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\mathrm{1}}{\mathrm{x}} \\ $$$$\mathrm{x}\rightarrow\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}} \\ $$$$\left(\mathrm{III}\right):\:\mathrm{f}\left(\mathrm{1}−\mathrm{x}\right)+\mathrm{f}\left(\frac{\mathrm{x}}{\mathrm{x}−\mathrm{1}}\right)=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}} \\ $$$$\left(\mathrm{III}\right)−\left(\mathrm{II}\right)=\mathrm{2f}\left(\mathrm{1}−\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}−\left(\frac{−\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\mathrm{1}}{\mathrm{x}}\right) \\ $$$$\mathrm{x}\rightarrow\mathrm{1}−\mathrm{x} \\ $$$$\mathrm{2f}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{x}}−\left(\frac{−\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} +\left(\mathrm{1}−\mathrm{x}\right)−\mathrm{1}}{\left(\mathrm{1}−\mathrm{x}\right)}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{x}}+\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}{\mathrm{1}−\mathrm{x}}=\frac{\mathrm{1}−\mathrm{x}+\mathrm{x}^{\mathrm{3}} −\mathrm{x}^{\mathrm{2}} +\mathrm{x}}{\mathrm{x}−\mathrm{x}^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{2f}\left(\mathrm{x}\right)=\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{1}−\mathrm{x}^{\mathrm{3}} }{\mathrm{x}^{\mathrm{2}} −\mathrm{x}} \\ $$
