Question Number 133206 by rexford last updated on 20/Feb/21
Answered by EDWIN88 last updated on 20/Feb/21
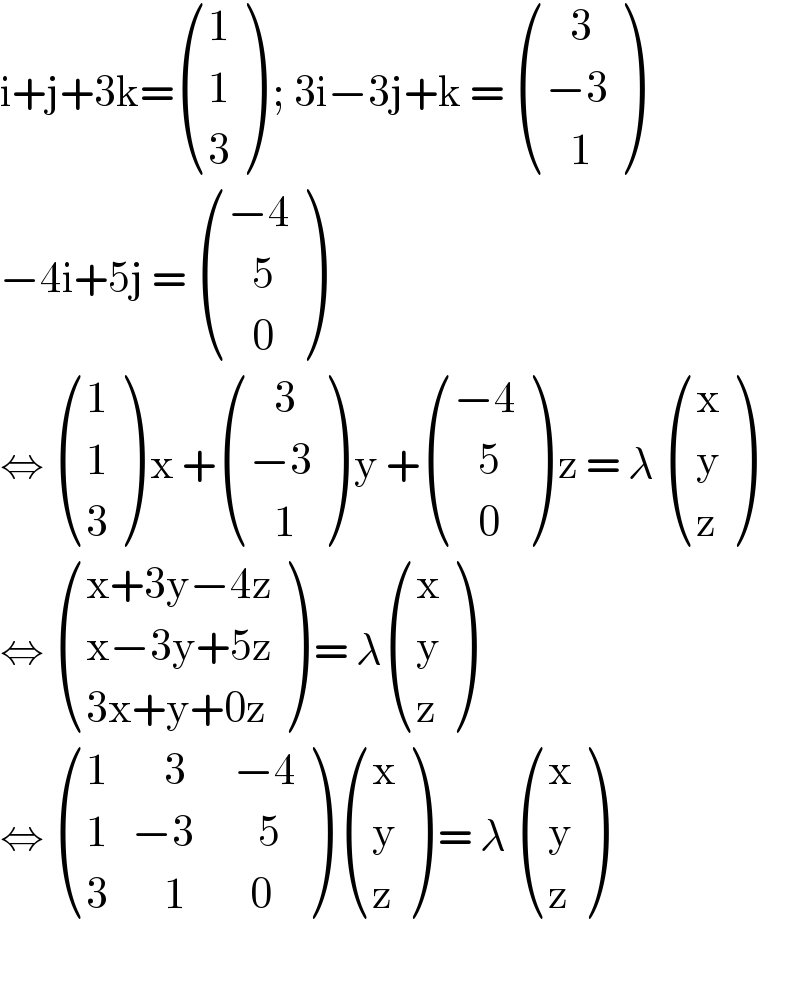
$$\mathrm{i}+\mathrm{j}+\mathrm{3k}=\begin{pmatrix}{\mathrm{1}}\\{\mathrm{1}}\\{\mathrm{3}}\end{pmatrix}\:;\:\mathrm{3i}−\mathrm{3j}+\mathrm{k}\:=\:\begin{pmatrix}{\:\:\:\mathrm{3}}\\{−\mathrm{3}}\\{\:\:\:\mathrm{1}}\end{pmatrix} \\ $$$$−\mathrm{4i}+\mathrm{5j}\:=\:\begin{pmatrix}{−\mathrm{4}}\\{\:\:\:\mathrm{5}}\\{\:\:\:\mathrm{0}}\end{pmatrix} \\ $$$$\Leftrightarrow\:\begin{pmatrix}{\mathrm{1}}\\{\mathrm{1}}\\{\mathrm{3}}\end{pmatrix}\:\mathrm{x}\:+\begin{pmatrix}{\:\:\:\mathrm{3}}\\{−\mathrm{3}}\\{\:\:\:\mathrm{1}}\end{pmatrix}\:\mathrm{y}\:+\begin{pmatrix}{−\mathrm{4}}\\{\:\:\:\mathrm{5}}\\{\:\:\:\mathrm{0}}\end{pmatrix}\:\mathrm{z}\:=\:\lambda\:\begin{pmatrix}{\mathrm{x}}\\{\mathrm{y}}\\{\mathrm{z}}\end{pmatrix} \\ $$$$\Leftrightarrow\:\begin{pmatrix}{\mathrm{x}+\mathrm{3y}−\mathrm{4z}}\\{\mathrm{x}−\mathrm{3y}+\mathrm{5z}}\\{\mathrm{3x}+\mathrm{y}+\mathrm{0z}}\end{pmatrix}\:=\:\lambda\begin{pmatrix}{\mathrm{x}}\\{\mathrm{y}}\\{\mathrm{z}}\end{pmatrix} \\ $$$$\Leftrightarrow\:\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\:\:\mathrm{3}\:\:\:\:\:\:−\mathrm{4}}\\{\mathrm{1}\:\:\:−\mathrm{3}\:\:\:\:\:\:\:\:\mathrm{5}}\\{\mathrm{3}\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\mathrm{0}}\end{pmatrix}\:\begin{pmatrix}{\mathrm{x}}\\{\mathrm{y}}\\{\mathrm{z}}\end{pmatrix}\:=\:\lambda\:\begin{pmatrix}{\mathrm{x}}\\{\mathrm{y}}\\{\mathrm{z}}\end{pmatrix} \\ $$$$ \\ $$
Answered by mr W last updated on 20/Feb/21
![[(1,3,(−4)),(1,(−3),5),(3,1,0) ] [(x),(y),(z) ]=λ [(x),(y),(z) ] [((1−λ),3,(−4)),(1,(−3−λ),5),(3,1,(0−λ)) ] [(x),(y),(z) ]=0 ∣ [((1−λ),3,(−4)),(1,(−3−λ),5),(3,1,(0−λ)) ]∣=0 (1−λ)(3λ+λ^2 −5)−3(−λ−15)−4(1+9+3λ)=0 (1−λ)(λ^2 +3λ−5)+5−8λ=0 λ^2 (λ+1)=0 ⇒λ=0, −1](https://www.tinkutara.com/question/Q133244.png)
$$\begin{bmatrix}{\mathrm{1}}&{\mathrm{3}}&{−\mathrm{4}}\\{\mathrm{1}}&{−\mathrm{3}}&{\mathrm{5}}\\{\mathrm{3}}&{\mathrm{1}}&{\mathrm{0}}\end{bmatrix}\begin{bmatrix}{{x}}\\{{y}}\\{{z}}\end{bmatrix}=\lambda\begin{bmatrix}{{x}}\\{{y}}\\{{z}}\end{bmatrix} \\ $$$$\begin{bmatrix}{\mathrm{1}−\lambda}&{\mathrm{3}}&{−\mathrm{4}}\\{\mathrm{1}}&{−\mathrm{3}−\lambda}&{\mathrm{5}}\\{\mathrm{3}}&{\mathrm{1}}&{\mathrm{0}−\lambda}\end{bmatrix}\begin{bmatrix}{{x}}\\{{y}}\\{{z}}\end{bmatrix}=\mathrm{0} \\ $$$$\mid\begin{bmatrix}{\mathrm{1}−\lambda}&{\mathrm{3}}&{−\mathrm{4}}\\{\mathrm{1}}&{−\mathrm{3}−\lambda}&{\mathrm{5}}\\{\mathrm{3}}&{\mathrm{1}}&{\mathrm{0}−\lambda}\end{bmatrix}\mid=\mathrm{0} \\ $$$$\left(\mathrm{1}−\lambda\right)\left(\mathrm{3}\lambda+\lambda^{\mathrm{2}} −\mathrm{5}\right)−\mathrm{3}\left(−\lambda−\mathrm{15}\right)−\mathrm{4}\left(\mathrm{1}+\mathrm{9}+\mathrm{3}\lambda\right)=\mathrm{0} \\ $$$$\left(\mathrm{1}−\lambda\right)\left(\lambda^{\mathrm{2}} +\mathrm{3}\lambda−\mathrm{5}\right)+\mathrm{5}−\mathrm{8}\lambda=\mathrm{0} \\ $$$$\lambda^{\mathrm{2}} \left(\lambda+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\lambda=\mathrm{0},\:−\mathrm{1} \\ $$
