Question Number 133240 by rexford last updated on 20/Feb/21
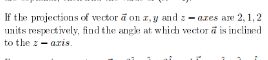
Answered by Kunal12588 last updated on 20/Feb/21
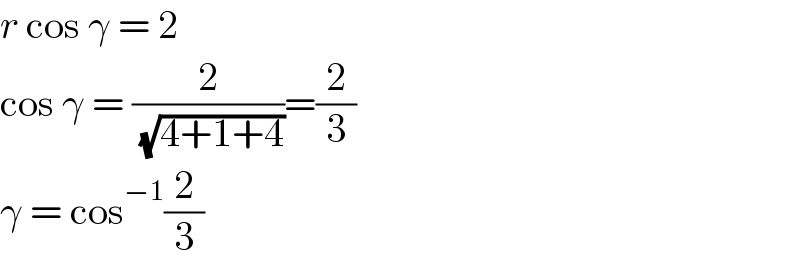
$${r}\:\mathrm{cos}\:\gamma\:=\:\mathrm{2} \\ $$$$\mathrm{cos}\:\gamma\:=\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{4}+\mathrm{1}+\mathrm{4}}}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\gamma\:=\:\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{2}}{\mathrm{3}} \\ $$
Answered by mr W last updated on 20/Feb/21
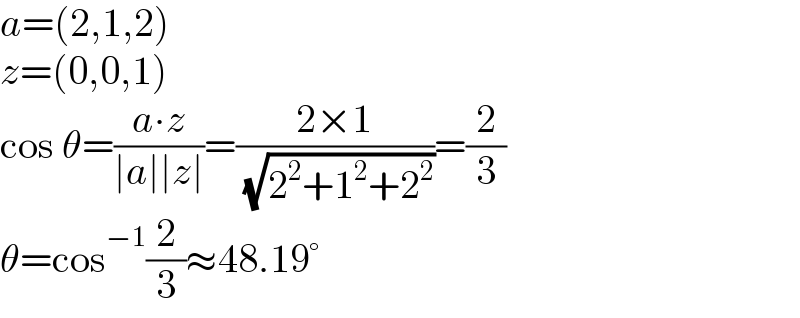
$${a}=\left(\mathrm{2},\mathrm{1},\mathrm{2}\right) \\ $$$${z}=\left(\mathrm{0},\mathrm{0},\mathrm{1}\right) \\ $$$$\mathrm{cos}\:\theta=\frac{{a}\centerdot{z}}{\mid{a}\mid\mid{z}\mid}=\frac{\mathrm{2}×\mathrm{1}}{\:\sqrt{\mathrm{2}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\theta=\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{2}}{\mathrm{3}}\approx\mathrm{48}.\mathrm{19}° \\ $$
