Question-133282

Question Number 133282 by rexford last updated on 20/Feb/21

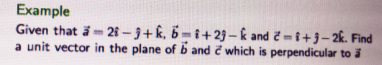
Answered by mr W last updated on 25/Feb/21

(b×c)×a =[(1,2,−1)×(1,1,−2)]×(2,−1,1) =(−3,1,−1)×(2,−1,1) =(0,1,1) as unit vector (0,((√2)/( 2)),((√2)/2))

$$\left(\boldsymbol{{b}}×\boldsymbol{{c}}\right)×\boldsymbol{{a}} \\ $$$$=\left[\left(\mathrm{1},\mathrm{2},−\mathrm{1}\right)×\left(\mathrm{1},\mathrm{1},−\mathrm{2}\right)\right]×\left(\mathrm{2},−\mathrm{1},\mathrm{1}\right) \\ $$$$=\left(−\mathrm{3},\mathrm{1},−\mathrm{1}\right)×\left(\mathrm{2},−\mathrm{1},\mathrm{1}\right) \\ $$$$=\left(\mathrm{0},\mathrm{1},\mathrm{1}\right) \\ $$$${as}\:{unit}\:{vector}\:\left(\mathrm{0},\frac{\sqrt{\mathrm{2}}}{\:\mathrm{2}},\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right) \\ $$

Answered by mr W last updated on 21/Feb/21

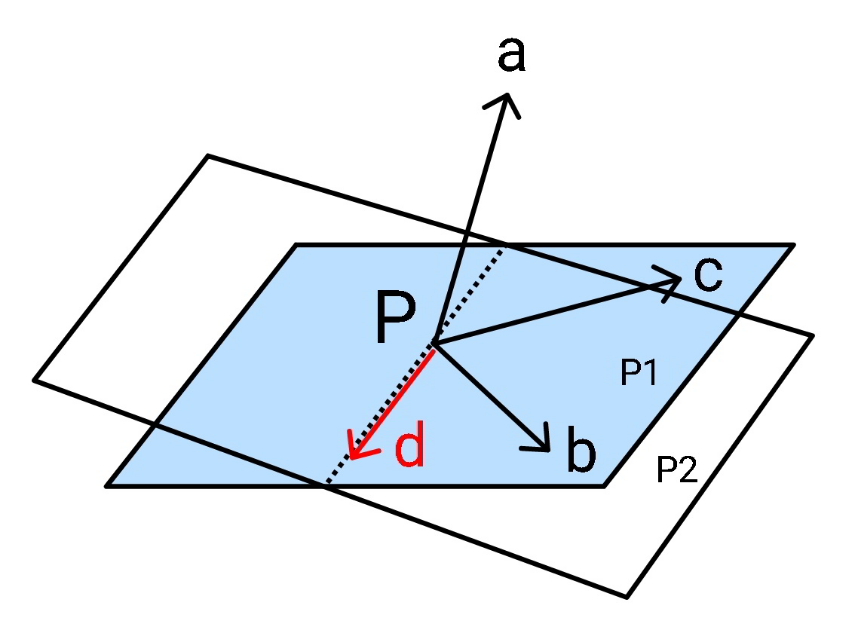
Commented by mr W last updated on 21/Feb/21

a=(2, −1, 1) b=(1, 2, −1) c=(1, 1, −2) say P(0, 0, 0) n_1 =b×c= determinant ((1,2,(−1)),(1,1,(−2)))=(−3, 1, −1) plane p_1 with normal n_1 : −3x+y−z=0 ...(i) n_2 =a=(2,−1, 1) plane p_2 with normal n_2 : 2x−y+z=0 ...(ii) intersection p_1 and p_2 : x=0 y=z d=(0, 1, 1) or as unit vector d=(0, ((√2)/2), ((√2)/2)) ⇒answer is ((√2)/2)j+((√2)/2)k

$$\boldsymbol{{a}}=\left(\mathrm{2},\:−\mathrm{1},\:\mathrm{1}\right) \\ $$$$\boldsymbol{{b}}=\left(\mathrm{1},\:\mathrm{2},\:−\mathrm{1}\right) \\ $$$$\boldsymbol{{c}}=\left(\mathrm{1},\:\mathrm{1},\:−\mathrm{2}\right) \\ $$$${say}\:{P}\left(\mathrm{0},\:\mathrm{0},\:\mathrm{0}\right) \\ $$$$\boldsymbol{{n}}_{\mathrm{1}} =\boldsymbol{{b}}×\boldsymbol{{c}}=\begin{vmatrix}{\mathrm{1}}&{\mathrm{2}}&{−\mathrm{1}}\\{\mathrm{1}}&{\mathrm{1}}&{−\mathrm{2}}\end{vmatrix}=\left(−\mathrm{3},\:\mathrm{1},\:−\mathrm{1}\right) \\ $$$${plane}\:{p}_{\mathrm{1}} \:{with}\:{normal}\:\boldsymbol{{n}}_{\mathrm{1}} : \\ $$$$−\mathrm{3}{x}+{y}−{z}=\mathrm{0}\:\:\:\:…\left({i}\right) \\ $$$$\boldsymbol{{n}}_{\mathrm{2}} =\boldsymbol{{a}}=\left(\mathrm{2},−\mathrm{1},\:\mathrm{1}\right) \\ $$$${plane}\:{p}_{\mathrm{2}} \:{with}\:{normal}\:\boldsymbol{{n}}_{\mathrm{2}} : \\ $$$$\mathrm{2}{x}−{y}+{z}=\mathrm{0}\:\:\:\:…\left({ii}\right) \\ $$$${intersection}\:{p}_{\mathrm{1}} \:{and}\:{p}_{\mathrm{2}} : \\ $$$${x}=\mathrm{0} \\ $$$${y}={z} \\ $$$$\boldsymbol{{d}}=\left(\mathrm{0},\:\mathrm{1},\:\mathrm{1}\right) \\ $$$${or}\:{as}\:{unit}\:{vector}\:\boldsymbol{{d}}=\left(\mathrm{0},\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}},\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right) \\ $$$$\Rightarrow{answer}\:{is}\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}{j}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}{k} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply