Question Number 133337 by mohammad17 last updated on 21/Feb/21

Commented by Dwaipayan Shikari last updated on 21/Feb/21

$${x}=\mathrm{3}\:{y}=\mathrm{1}\:{z}=\mathrm{2} \\ $$
Commented by mohammad17 last updated on 21/Feb/21
$${can}\:{you}\:{give}\:{me}\:{stebs} \\ $$
Commented by Dwaipayan Shikari last updated on 21/Feb/21
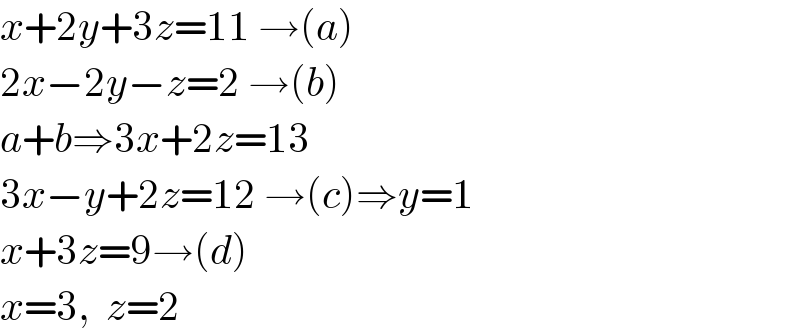
$${x}+\mathrm{2}{y}+\mathrm{3}{z}=\mathrm{11}\:\rightarrow\left({a}\right) \\ $$$$\mathrm{2}{x}−\mathrm{2}{y}−{z}=\mathrm{2}\:\rightarrow\left({b}\right) \\ $$$${a}+{b}\Rightarrow\mathrm{3}{x}+\mathrm{2}{z}=\mathrm{13} \\ $$$$\mathrm{3}{x}−{y}+\mathrm{2}{z}=\mathrm{12}\:\rightarrow\left({c}\right)\Rightarrow{y}=\mathrm{1} \\ $$$${x}+\mathrm{3}{z}=\mathrm{9}\rightarrow\left({d}\right) \\ $$$${x}=\mathrm{3},\:\:{z}=\mathrm{2} \\ $$
Commented by mohammad17 last updated on 21/Feb/21
$${please}\:{sir}\:{help}\:{me} \\ $$
Commented by bramlexs22 last updated on 21/Feb/21
$$\mathrm{this}\:\mathrm{not}\:\mathrm{triangular}\:\mathrm{decomposition} \\ $$
Answered by bramlexs22 last updated on 21/Feb/21
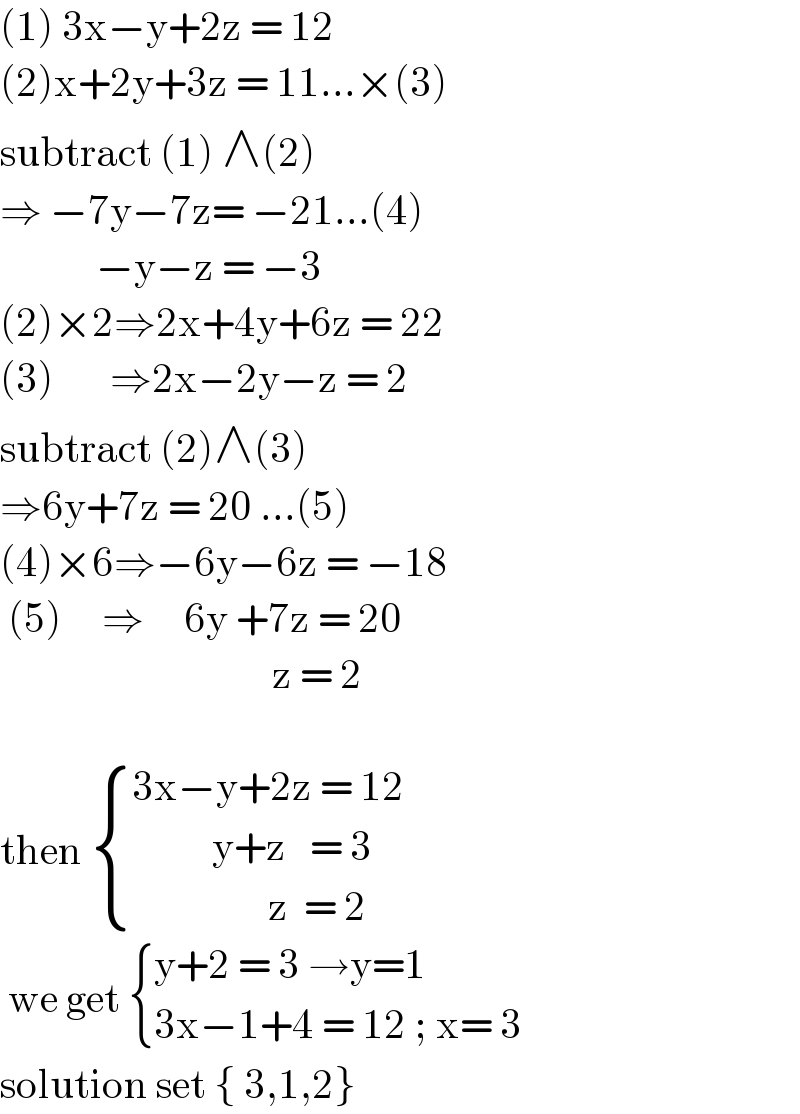
$$\left(\mathrm{1}\right)\:\mathrm{3x}−\mathrm{y}+\mathrm{2z}\:=\:\mathrm{12}\: \\ $$$$\left(\mathrm{2}\right)\mathrm{x}+\mathrm{2y}+\mathrm{3z}\:=\:\mathrm{11}…×\left(\mathrm{3}\right) \\ $$$$\mathrm{subtract}\:\left(\mathrm{1}\right)\:\wedge\left(\mathrm{2}\right) \\ $$$$\Rightarrow\:−\mathrm{7y}−\mathrm{7z}=\:−\mathrm{21}…\left(\mathrm{4}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{y}−\mathrm{z}\:=\:−\mathrm{3} \\ $$$$\left(\mathrm{2}\right)×\mathrm{2}\Rightarrow\mathrm{2x}+\mathrm{4y}+\mathrm{6z}\:=\:\mathrm{22} \\ $$$$\left(\mathrm{3}\right)\:\:\:\:\:\:\:\Rightarrow\mathrm{2x}−\mathrm{2y}−\mathrm{z}\:=\:\mathrm{2} \\ $$$$\mathrm{subtract}\:\left(\mathrm{2}\right)\wedge\left(\mathrm{3}\right) \\ $$$$\Rightarrow\mathrm{6y}+\mathrm{7z}\:=\:\mathrm{20}\:…\left(\mathrm{5}\right) \\ $$$$\left(\mathrm{4}\right)×\mathrm{6}\Rightarrow−\mathrm{6y}−\mathrm{6z}\:=\:−\mathrm{18} \\ $$$$\:\left(\mathrm{5}\right)\:\:\:\:\:\Rightarrow\:\:\:\:\:\mathrm{6y}\:+\mathrm{7z}\:=\:\mathrm{20} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{z}\:=\:\mathrm{2} \\ $$$$ \\ $$$$\mathrm{then}\:\begin{cases}{\mathrm{3x}−\mathrm{y}+\mathrm{2z}\:=\:\mathrm{12}}\\{\:\:\:\:\:\:\:\:\:\:\mathrm{y}+\mathrm{z}\:\:\:=\:\mathrm{3}}\\{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{z}\:\:=\:\mathrm{2}}\end{cases} \\ $$$$\:\mathrm{we}\:\mathrm{get}\:\begin{cases}{\mathrm{y}+\mathrm{2}\:=\:\mathrm{3}\:\rightarrow\mathrm{y}=\mathrm{1}}\\{\mathrm{3x}−\mathrm{1}+\mathrm{4}\:=\:\mathrm{12}\:;\:\mathrm{x}=\:\mathrm{3}}\end{cases} \\ $$$$\mathrm{solution}\:\mathrm{set}\:\left\{\:\mathrm{3},\mathrm{1},\mathrm{2}\right\} \\ $$
