Question Number 133394 by Dwaipayan Shikari last updated on 21/Feb/21
Commented by Dwaipayan Shikari last updated on 21/Feb/21
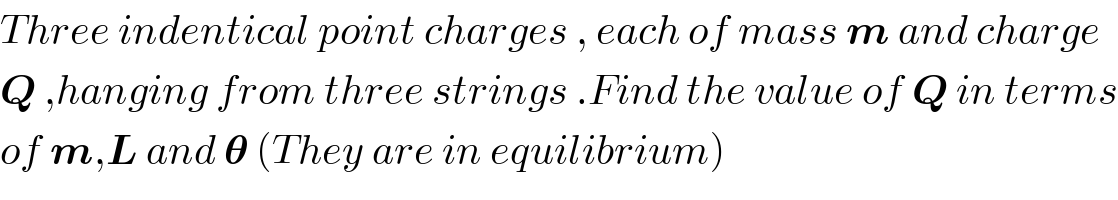
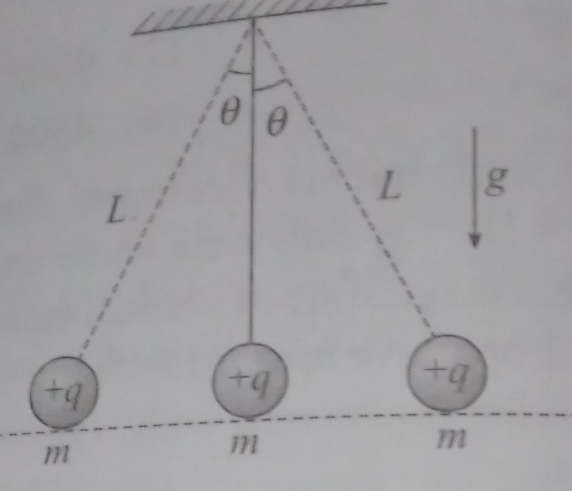
$${Three}\:{indentical}\:{point}\:{charges}\:,\:{each}\:{of}\:{mass}\:\boldsymbol{{m}}\:{and}\:{charge} \\ $$$$\boldsymbol{{Q}}\:,{hanging}\:{from}\:{three}\:{strings}\:.{Find}\:{the}\:{value}\:{of}\:\boldsymbol{{Q}}\:{in}\:{terms} \\ $$$${of}\:\boldsymbol{{m}},\boldsymbol{{L}}\:{and}\:\boldsymbol{\theta}\:\left({They}\:{are}\:{in}\:{equilibrium}\right) \\ $$
Commented by Dwaipayan Shikari last updated on 21/Feb/21
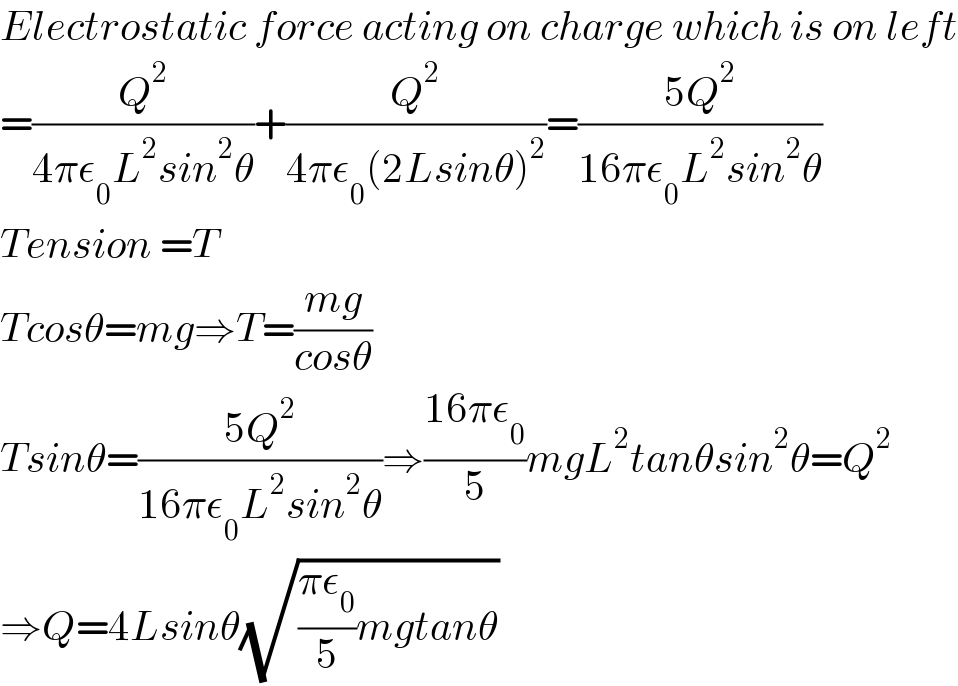
$${Electrostatic}\:{force}\:{acting}\:{on}\:{charge}\:{which}\:{is}\:{on}\:{left} \\ $$$$=\frac{{Q}^{\mathrm{2}} }{\mathrm{4}\pi\epsilon_{\mathrm{0}} {L}^{\mathrm{2}} {sin}^{\mathrm{2}} \theta}+\frac{{Q}^{\mathrm{2}} }{\mathrm{4}\pi\epsilon_{\mathrm{0}} \left(\mathrm{2}{Lsin}\theta\right)^{\mathrm{2}} }=\frac{\mathrm{5}{Q}^{\mathrm{2}} }{\mathrm{16}\pi\epsilon_{\mathrm{0}} {L}^{\mathrm{2}} {sin}^{\mathrm{2}} \theta} \\ $$$${Tension}\:={T}\: \\ $$$${Tcos}\theta={mg}\Rightarrow{T}=\frac{{mg}}{{cos}\theta} \\ $$$${Tsin}\theta=\frac{\mathrm{5}{Q}^{\mathrm{2}} }{\mathrm{16}\pi\epsilon_{\mathrm{0}} {L}^{\mathrm{2}} {sin}^{\mathrm{2}} \theta}\Rightarrow\frac{\mathrm{16}\pi\epsilon_{\mathrm{0}} }{\mathrm{5}}{mgL}^{\mathrm{2}} {tan}\theta{sin}^{\mathrm{2}} \theta={Q}^{\mathrm{2}} \\ $$$$\Rightarrow{Q}=\mathrm{4}{Lsin}\theta\sqrt{\frac{\pi\epsilon_{\mathrm{0}} }{\mathrm{5}}{mgtan}\theta} \\ $$
Commented by Dwaipayan Shikari last updated on 22/Feb/21

$${Is}\:{it}\:{true}? \\ $$
