Question Number 133423 by mathlove last updated on 22/Feb/21

Commented by liki last updated on 24/Feb/21
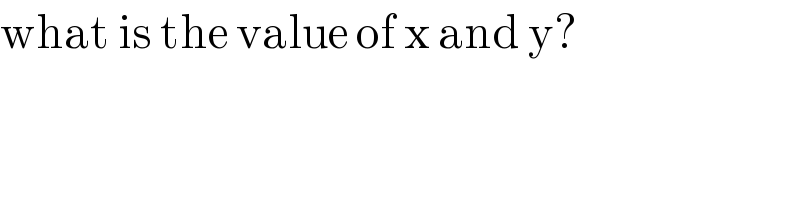
$$\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{x}\:\mathrm{and}\:\mathrm{y}? \\ $$
Commented by MJS_new last updated on 24/Feb/21
I gave the answer 2 days ago. What's the problem?
Commented by liki last updated on 24/Feb/21

$$\mathrm{sory}\:\mathrm{sir}\:\mathrm{i}\:\mathrm{did}\:\mathrm{not}\:\mathrm{see}\:\mathrm{the}\:\mathrm{answer}\: \\ $$
Commented by liki last updated on 24/Feb/21
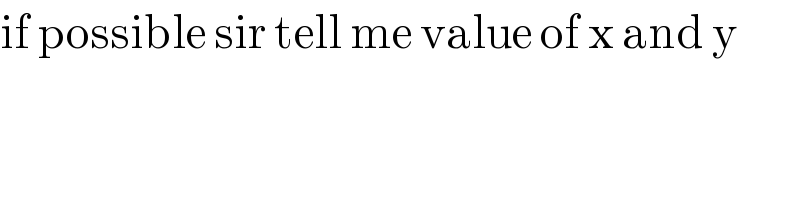
$$\mathrm{if}\:\mathrm{possible}\:\mathrm{sir}\:\mathrm{tell}\:\mathrm{me}\:\mathrm{value}\:\mathrm{of}\:\mathrm{x}\:\mathrm{and}\:\mathrm{y} \\ $$
Answered by MJS_new last updated on 24/Feb/21
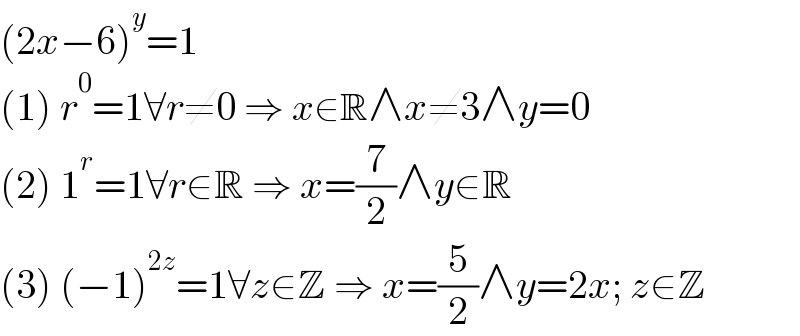
$$\left(\mathrm{2}{x}−\mathrm{6}\right)^{{y}} =\mathrm{1} \\ $$$$\left(\mathrm{1}\right)\:{r}^{\mathrm{0}} =\mathrm{1}\forall{r}\neq\mathrm{0}\:\Rightarrow\:{x}\in\mathbb{R}\wedge{x}\neq\mathrm{3}\wedge{y}=\mathrm{0} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{1}^{{r}} =\mathrm{1}\forall{r}\in\mathbb{R}\:\Rightarrow\:{x}=\frac{\mathrm{7}}{\mathrm{2}}\wedge{y}\in\mathbb{R} \\ $$$$\left(\mathrm{3}\right)\:\left(−\mathrm{1}\right)^{\mathrm{2}{z}} =\mathrm{1}\forall{z}\in\mathbb{Z}\:\Rightarrow\:{x}=\frac{\mathrm{5}}{\mathrm{2}}\wedge{y}=\mathrm{2}{x};\:{z}\in\mathbb{Z} \\ $$
Commented by MJS_new last updated on 24/Feb/21
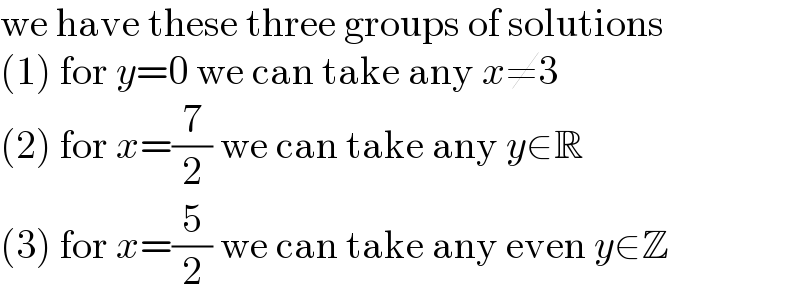
$$\mathrm{we}\:\mathrm{have}\:\mathrm{these}\:\mathrm{three}\:\mathrm{groups}\:\mathrm{of}\:\mathrm{solutions} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{for}\:{y}=\mathrm{0}\:\mathrm{we}\:\mathrm{can}\:\mathrm{take}\:\mathrm{any}\:{x}\neq\mathrm{3} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{for}\:{x}=\frac{\mathrm{7}}{\mathrm{2}}\:\mathrm{we}\:\mathrm{can}\:\mathrm{take}\:\mathrm{any}\:{y}\in\mathbb{R} \\ $$$$\left(\mathrm{3}\right)\:\mathrm{for}\:{x}=\frac{\mathrm{5}}{\mathrm{2}}\:\mathrm{we}\:\mathrm{can}\:\mathrm{take}\:\mathrm{any}\:\mathrm{even}\:{y}\in\mathbb{Z} \\ $$
