Question Number 133431 by Algoritm last updated on 22/Feb/21
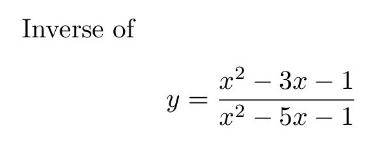
Answered by benjo_mathlover last updated on 22/Feb/21
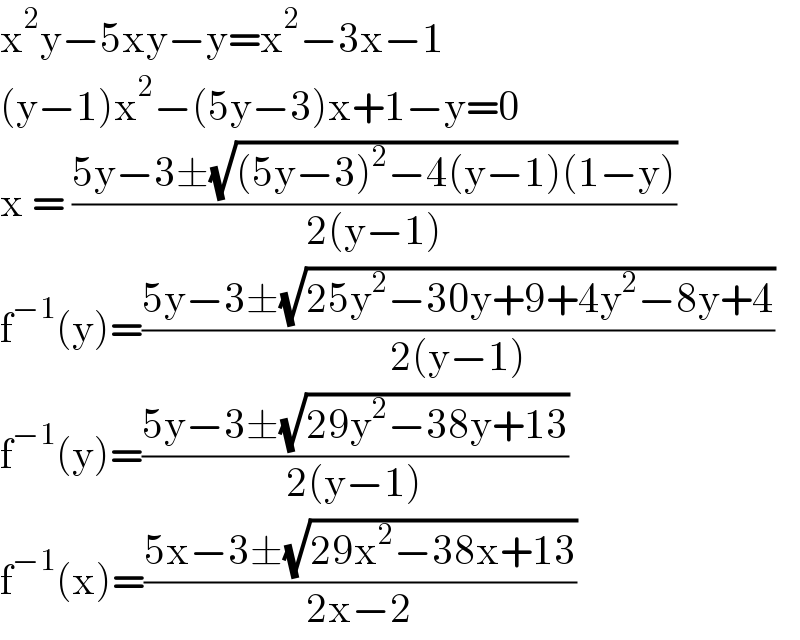
$$\mathrm{x}^{\mathrm{2}} \mathrm{y}−\mathrm{5xy}−\mathrm{y}=\mathrm{x}^{\mathrm{2}} −\mathrm{3x}−\mathrm{1} \\ $$$$\left(\mathrm{y}−\mathrm{1}\right)\mathrm{x}^{\mathrm{2}} −\left(\mathrm{5y}−\mathrm{3}\right)\mathrm{x}+\mathrm{1}−\mathrm{y}=\mathrm{0} \\ $$$$\mathrm{x}\:=\:\frac{\mathrm{5y}−\mathrm{3}\pm\sqrt{\left(\mathrm{5y}−\mathrm{3}\right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{y}−\mathrm{1}\right)\left(\mathrm{1}−\mathrm{y}\right)}}{\mathrm{2}\left(\mathrm{y}−\mathrm{1}\right)} \\ $$$$\mathrm{f}^{−\mathrm{1}} \left(\mathrm{y}\right)=\frac{\mathrm{5y}−\mathrm{3}\pm\sqrt{\mathrm{25y}^{\mathrm{2}} −\mathrm{30y}+\mathrm{9}+\mathrm{4y}^{\mathrm{2}} −\mathrm{8y}+\mathrm{4}}}{\mathrm{2}\left(\mathrm{y}−\mathrm{1}\right)} \\ $$$$\mathrm{f}^{−\mathrm{1}} \left(\mathrm{y}\right)=\frac{\mathrm{5y}−\mathrm{3}\pm\sqrt{\mathrm{29y}^{\mathrm{2}} −\mathrm{38y}+\mathrm{13}}}{\mathrm{2}\left(\mathrm{y}−\mathrm{1}\right)} \\ $$$$\mathrm{f}^{−\mathrm{1}} \left(\mathrm{x}\right)=\frac{\mathrm{5x}−\mathrm{3}\pm\sqrt{\mathrm{29x}^{\mathrm{2}} −\mathrm{38x}+\mathrm{13}}}{\mathrm{2x}−\mathrm{2}} \\ $$
Answered by Dwaipayan Shikari last updated on 22/Feb/21
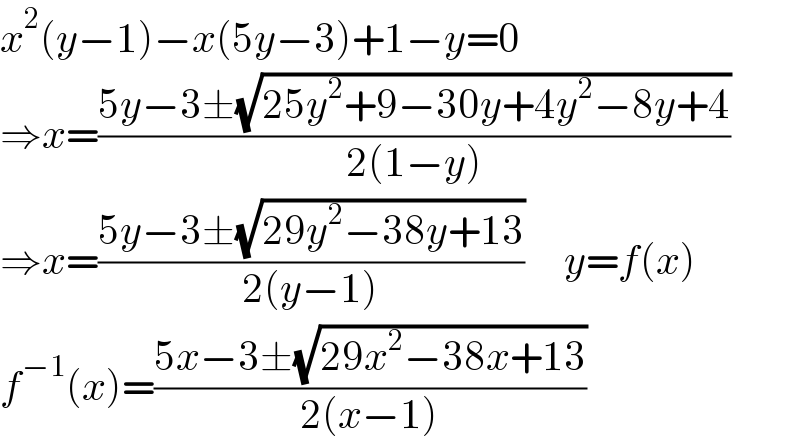
$${x}^{\mathrm{2}} \left({y}−\mathrm{1}\right)−{x}\left(\mathrm{5}{y}−\mathrm{3}\right)+\mathrm{1}−{y}=\mathrm{0}\: \\ $$$$\Rightarrow{x}=\frac{\mathrm{5}{y}−\mathrm{3}\pm\sqrt{\mathrm{25}{y}^{\mathrm{2}} +\mathrm{9}−\mathrm{30}{y}+\mathrm{4}{y}^{\mathrm{2}} −\mathrm{8}{y}+\mathrm{4}}}{\mathrm{2}\left(\mathrm{1}−{y}\right)} \\ $$$$\Rightarrow{x}=\frac{\mathrm{5}{y}−\mathrm{3}\pm\sqrt{\mathrm{29}{y}^{\mathrm{2}} −\mathrm{38}{y}+\mathrm{13}}}{\mathrm{2}\left({y}−\mathrm{1}\right)}\:\:\:\:\:{y}={f}\left({x}\right) \\ $$$${f}^{−\mathrm{1}} \left({x}\right)=\frac{\mathrm{5}{x}−\mathrm{3}\pm\sqrt{\mathrm{29}{x}^{\mathrm{2}} −\mathrm{38}{x}+\mathrm{13}}}{\mathrm{2}\left({x}−\mathrm{1}\right)} \\ $$
