Question Number 133440 by bagjagunawan last updated on 22/Feb/21
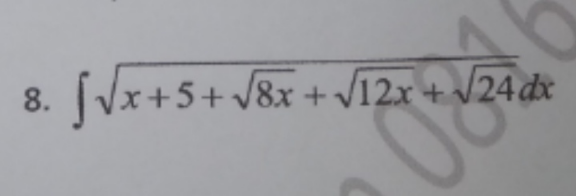
Answered by Ar Brandon last updated on 22/Feb/21
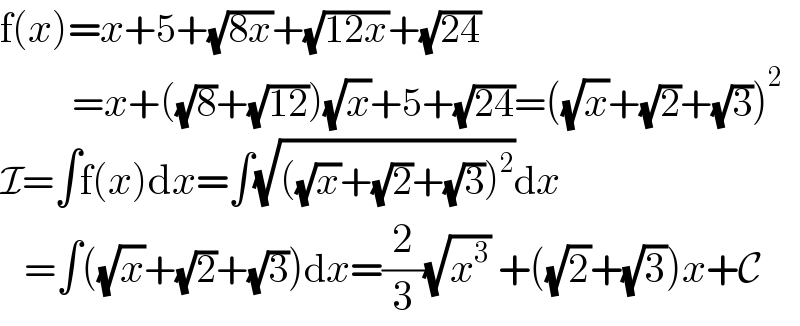
$$\mathrm{f}\left({x}\right)={x}+\mathrm{5}+\sqrt{\mathrm{8}{x}}+\sqrt{\mathrm{12}{x}}+\sqrt{\mathrm{24}}\: \\ $$$$\:\:\:\:\:\:\:\:\:={x}+\left(\sqrt{\mathrm{8}}+\sqrt{\mathrm{12}}\right)\sqrt{{x}}+\mathrm{5}+\sqrt{\mathrm{24}}=\left(\sqrt{{x}}+\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \\ $$$$\mathcal{I}=\int\mathrm{f}\left({x}\right)\mathrm{d}{x}=\int\sqrt{\left(\sqrt{{x}}+\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }\mathrm{d}{x} \\ $$$$\:\:\:=\int\left(\sqrt{{x}}+\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}\right)\mathrm{d}{x}=\frac{\mathrm{2}}{\mathrm{3}}\sqrt{{x}^{\mathrm{3}} }\:+\left(\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}\right){x}+\mathcal{C} \\ $$
Commented by bagjagunawan last updated on 22/Feb/21

$$\mathrm{Wow}\: \\ $$$$\mathrm{thank}\:\mathrm{you}\:\mathrm{Sir} \\ $$
Commented by Ar Brandon last updated on 22/Feb/21
You're welcome
