Question-133487

Question Number 133487 by mr W last updated on 22/Feb/21

Commented by mr W last updated on 22/Feb/21

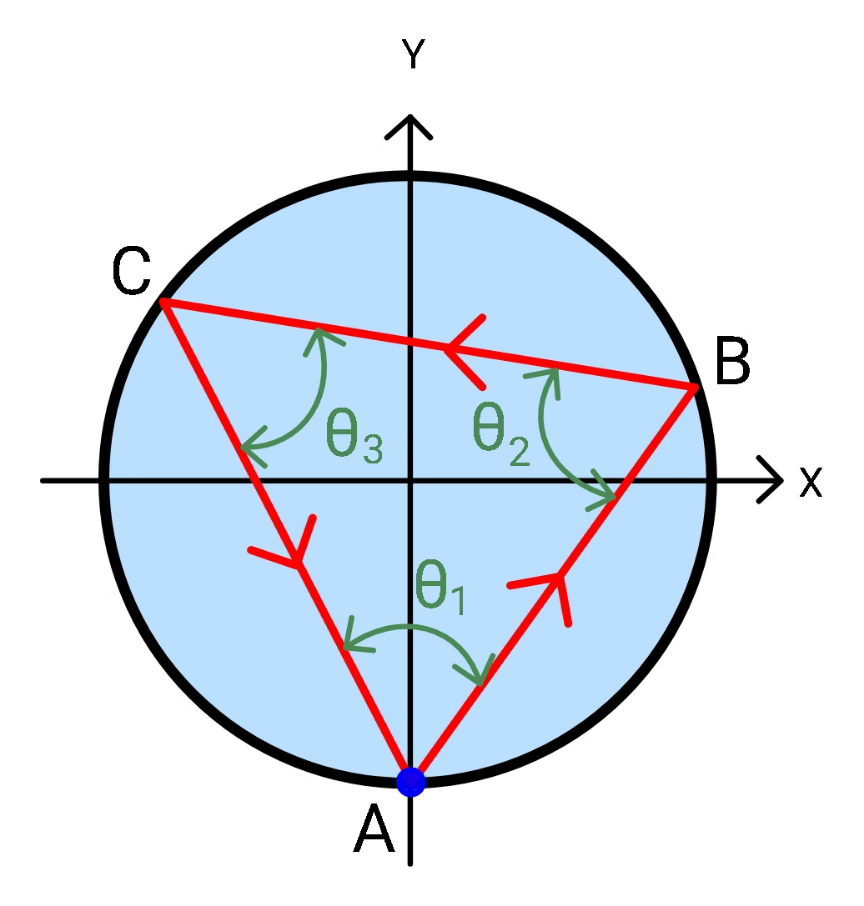
$${a}\:{ball}\:{is}\:{projected}\:{along}\:{the}\:{smooth} \\ $$$${floor}\:{and}\:{returns}\:{back}\:{after}\:{two} \\ $$$${times}\:{impact}\:{with}\:{the}\:{circular}\:{wall}. \\ $$$${if}\:{the}\:{restitution}\:{coefficient}\:{is}\:{e}, \\ $$$${find}\:{the}\:{angles}\:{of}\:\Delta{ABC}. \\ $$

Answered by mr W last updated on 22/Feb/21

Commented by mr W last updated on 23/Feb/21

at point B: tan β=((tan α)/e) at point C: tan γ=((tan β)/e)=((tan α)/e^2 ) 2(α+β+γ=π ⇒α+β=(π/2)−γ tan (α+β)=tan ((π/2)−γ)=(1/(tan γ)) ((tan α+((tan α)/e))/(1−((tan^2 α)/e)))=(1/((tan α)/e^2 )) (((1+e)tan α)/(e−tan^2 α))=(e^2 /(tan α)) (1+e+e^2 )tan^2 α=e^3 ⇒tan α=e(√(e/(1+e+e^2 ))) ⇒tan β=(√(e/(1+e+e^2 ))) ⇒tan γ=(1/e)(√(e/(1+e+e^2 ))) tan (α+β)=(((1+e)(√(e/(1+e+e^2 ))))/(1−e×(e/(1+e+e^2 ))))=(√(e(1+e+e^2 ))) tan (β+γ)=(((1+(1/e))(√(e/(1+e+e^2 ))))/(1−(1/e)×(e/(1+e+e^2 ))))=((√(e(1+e+e^2 )))/e^2 ) tan (γ+α)=((((1/e)+e)(√(e/(1+e+e^2 ))))/(1−(e/(1+e+e^2 ))))=((√(e(1+e+e^2 )))/e) ⇒θ_1 =γ+α=tan^(−1) ((√(e(1+e+e^2 )))/e) ⇒θ_2 =α+β=tan^(−1) (√(e(1+e+e^2 ))) ⇒θ_3 =β+γ=tan^(−1) ((√(e(1+e+e^2 )))/e^2 ) example: e=0.5 θ_1 =tan^(−1) ((√(14))/2)=61.87° θ_2 =tan^(−1) ((√(14))/4)=43.09° θ_3 =tan^(−1) (√(14))=75.04°

$${at}\:{point}\:{B}: \\ $$$$\mathrm{tan}\:\beta=\frac{\mathrm{tan}\:\alpha}{{e}} \\ $$$${at}\:{point}\:{C}: \\ $$$$\mathrm{tan}\:\gamma=\frac{\mathrm{tan}\:\beta}{{e}}=\frac{\mathrm{tan}\:\alpha}{{e}^{\mathrm{2}} } \\ $$$$\mathrm{2}\left(\alpha+\beta+\gamma=\pi\right. \\ $$$$\Rightarrow\alpha+\beta=\frac{\pi}{\mathrm{2}}−\gamma \\ $$$$\mathrm{tan}\:\left(\alpha+\beta\right)=\mathrm{tan}\:\left(\frac{\pi}{\mathrm{2}}−\gamma\right)=\frac{\mathrm{1}}{\mathrm{tan}\:\gamma} \\ $$$$\frac{\mathrm{tan}\:\alpha+\frac{\mathrm{tan}\:\alpha}{{e}}}{\mathrm{1}−\frac{\mathrm{tan}^{\mathrm{2}} \:\alpha}{{e}}}=\frac{\mathrm{1}}{\frac{\mathrm{tan}\:\alpha}{{e}^{\mathrm{2}} }} \\ $$$$\frac{\left(\mathrm{1}+{e}\right)\mathrm{tan}\:\alpha}{{e}−\mathrm{tan}^{\mathrm{2}} \:\alpha}=\frac{{e}^{\mathrm{2}} }{\mathrm{tan}\:\alpha} \\ $$$$\left(\mathrm{1}+{e}+{e}^{\mathrm{2}} \right)\mathrm{tan}^{\mathrm{2}} \:\alpha={e}^{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{tan}\:\alpha={e}\sqrt{\frac{{e}}{\mathrm{1}+{e}+{e}^{\mathrm{2}} }} \\ $$$$\Rightarrow\mathrm{tan}\:\beta=\sqrt{\frac{{e}}{\mathrm{1}+{e}+{e}^{\mathrm{2}} }} \\ $$$$\Rightarrow\mathrm{tan}\:\gamma=\frac{\mathrm{1}}{{e}}\sqrt{\frac{{e}}{\mathrm{1}+{e}+{e}^{\mathrm{2}} }} \\ $$$$\mathrm{tan}\:\left(\alpha+\beta\right)=\frac{\left(\mathrm{1}+{e}\right)\sqrt{\frac{{e}}{\mathrm{1}+{e}+{e}^{\mathrm{2}} }}}{\mathrm{1}−{e}×\frac{{e}}{\mathrm{1}+{e}+{e}^{\mathrm{2}} }}=\sqrt{{e}\left(\mathrm{1}+{e}+{e}^{\mathrm{2}} \right)} \\ $$$$\mathrm{tan}\:\left(\beta+\gamma\right)=\frac{\left(\mathrm{1}+\frac{\mathrm{1}}{{e}}\right)\sqrt{\frac{{e}}{\mathrm{1}+{e}+{e}^{\mathrm{2}} }}}{\mathrm{1}−\frac{\mathrm{1}}{{e}}×\frac{{e}}{\mathrm{1}+{e}+{e}^{\mathrm{2}} }}=\frac{\sqrt{{e}\left(\mathrm{1}+{e}+{e}^{\mathrm{2}} \right)}}{{e}^{\mathrm{2}} } \\ $$$$\mathrm{tan}\:\left(\gamma+\alpha\right)=\frac{\left(\frac{\mathrm{1}}{{e}}+{e}\right)\sqrt{\frac{{e}}{\mathrm{1}+{e}+{e}^{\mathrm{2}} }}}{\mathrm{1}−\frac{{e}}{\mathrm{1}+{e}+{e}^{\mathrm{2}} }}=\frac{\sqrt{{e}\left(\mathrm{1}+{e}+{e}^{\mathrm{2}} \right)}}{{e}} \\ $$$$\Rightarrow\theta_{\mathrm{1}} =\gamma+\alpha=\mathrm{tan}^{−\mathrm{1}} \frac{\sqrt{{e}\left(\mathrm{1}+{e}+{e}^{\mathrm{2}} \right)}}{{e}} \\ $$$$\Rightarrow\theta_{\mathrm{2}} =\alpha+\beta=\mathrm{tan}^{−\mathrm{1}} \sqrt{{e}\left(\mathrm{1}+{e}+{e}^{\mathrm{2}} \right)} \\ $$$$\Rightarrow\theta_{\mathrm{3}} =\beta+\gamma=\mathrm{tan}^{−\mathrm{1}} \frac{\sqrt{{e}\left(\mathrm{1}+{e}+{e}^{\mathrm{2}} \right)}}{{e}^{\mathrm{2}} } \\ $$$${example}:\:{e}=\mathrm{0}.\mathrm{5} \\ $$$$\theta_{\mathrm{1}} =\mathrm{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{14}}}{\mathrm{2}}=\mathrm{61}.\mathrm{87}° \\ $$$$\theta_{\mathrm{2}} =\mathrm{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{14}}}{\mathrm{4}}=\mathrm{43}.\mathrm{09}° \\ $$$$\theta_{\mathrm{3}} =\mathrm{tan}^{−\mathrm{1}} \sqrt{\mathrm{14}}=\mathrm{75}.\mathrm{04}° \\ $$

Commented by mr W last updated on 23/Feb/21