Question-133518

Question Number 133518 by Abdoulaye last updated on 22/Feb/21

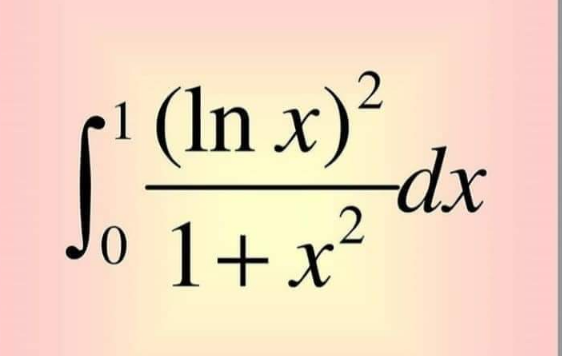
Answered by mnjuly1970 last updated on 22/Feb/21

$${ans}:\:\frac{\pi^{\mathrm{3}} }{\mathrm{16}} \\ $$

Answered by Dwaipayan Shikari last updated on 22/Feb/21

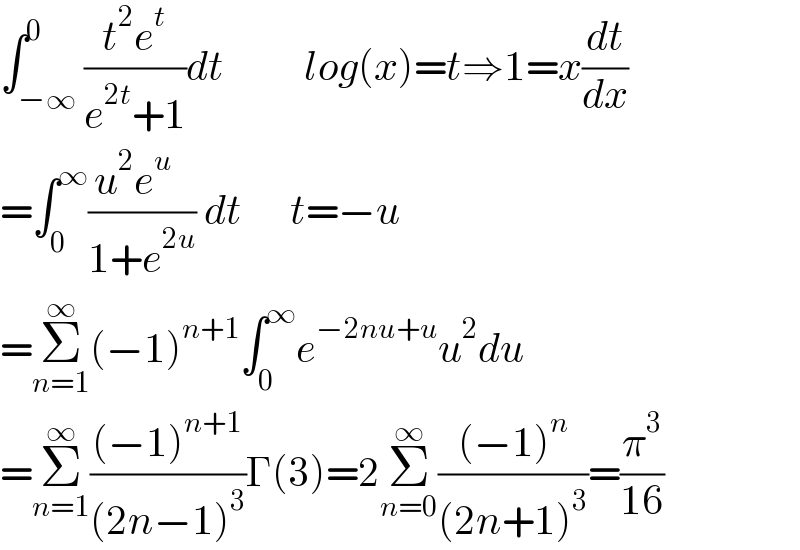
∫_(−∞) ^0 ((t^2 e^t )/(e^(2t) +1))dt log(x)=t⇒1=x(dt/dx) =∫_0 ^∞ ((u^2 e^u )/(1+e^(2u) )) dt t=−u =Σ_(n=1) ^∞ (−1)^(n+1) ∫_0 ^∞ e^(−2nu+u) u^2 du =Σ_(n=1) ^∞ (((−1)^(n+1) )/((2n−1)^3 ))Γ(3)=2Σ_(n=0) ^∞ (((−1)^n )/((2n+1)^3 ))=(π^3 /(16))

$$\int_{−\infty} ^{\mathrm{0}} \frac{{t}^{\mathrm{2}} {e}^{{t}} }{{e}^{\mathrm{2}{t}} +\mathrm{1}}{dt}\:\:\:\:\:\:\:\:\:\:{log}\left({x}\right)={t}\Rightarrow\mathrm{1}={x}\frac{{dt}}{{dx}} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{{u}^{\mathrm{2}} {e}^{{u}} \:\:}{\mathrm{1}+{e}^{\mathrm{2}{u}} }\:{dt}\:\:\:\:\:\:{t}=−{u} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{2}{nu}+{u}} {u}^{\mathrm{2}} {du} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{3}} }\Gamma\left(\mathrm{3}\right)=\mathrm{2}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{3}} }=\frac{\pi^{\mathrm{3}} }{\mathrm{16}} \\ $$

Commented by Dwaipayan Shikari last updated on 22/Feb/21

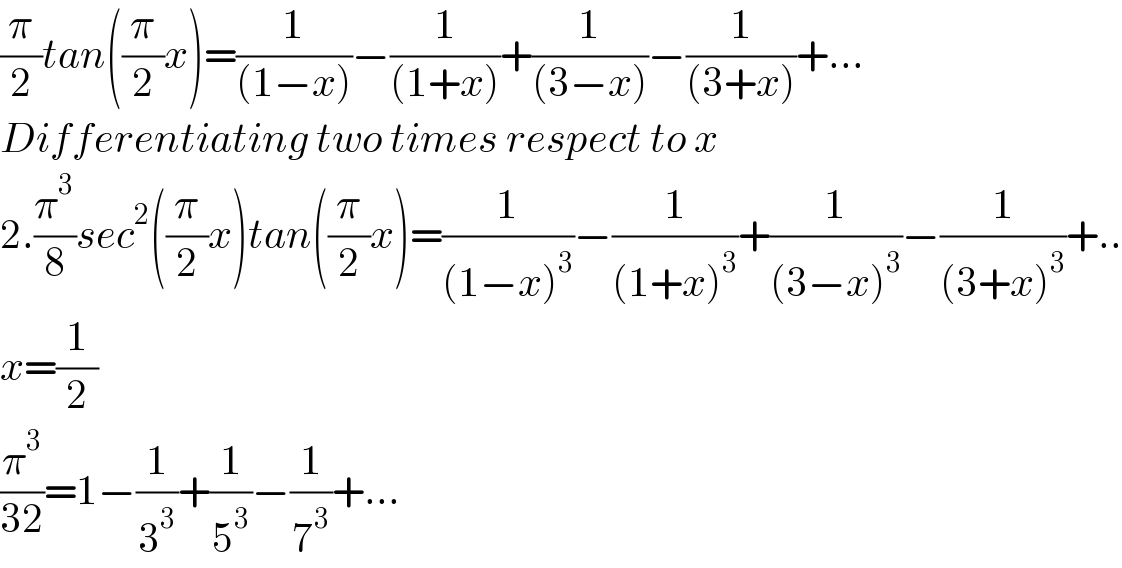
(π/2)tan((π/2)x)=(1/((1−x)))−(1/((1+x)))+(1/((3−x)))−(1/((3+x)))+... Differentiating two times respect to x 2.(π^3 /8)sec^2 ((π/2)x)tan((π/2)x)=(1/((1−x)^3 ))−(1/((1+x)^3 ))+(1/((3−x)^3 ))−(1/((3+x)^3 ))+.. x=(1/2) (π^3 /(32))=1−(1/3^3 )+(1/5^3 )−(1/7^3 )+...

$$\frac{\pi}{\mathrm{2}}{tan}\left(\frac{\pi}{\mathrm{2}}{x}\right)=\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)}−\frac{\mathrm{1}}{\left(\mathrm{1}+{x}\right)}+\frac{\mathrm{1}}{\left(\mathrm{3}−{x}\right)}−\frac{\mathrm{1}}{\left(\mathrm{3}+{x}\right)}+… \\ $$$${Differentiating}\:{two}\:{times}\:{respect}\:{to}\:{x} \\ $$$$\mathrm{2}.\frac{\pi^{\mathrm{3}} }{\mathrm{8}}{sec}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}}{x}\right){tan}\left(\frac{\pi}{\mathrm{2}}{x}\right)=\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }−\frac{\mathrm{1}}{\left(\mathrm{1}+{x}\right)^{\mathrm{3}} }+\frac{\mathrm{1}}{\left(\mathrm{3}−{x}\right)^{\mathrm{3}} }−\frac{\mathrm{1}}{\left(\mathrm{3}+{x}\right)^{\mathrm{3}} }+.. \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{\pi^{\mathrm{3}} }{\mathrm{32}}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{3}} }−\frac{\mathrm{1}}{\mathrm{7}^{\mathrm{3}} }+… \\ $$

Commented by Abdoulaye last updated on 22/Feb/21

$${what}\:{it}'{s}\:\Gamma? \\ $$

Commented by Dwaipayan Shikari last updated on 22/Feb/21

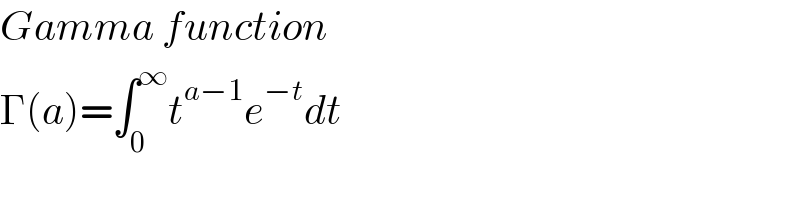
Gamma function Γ(a)=∫_0 ^∞ t^(a−1) e^(−t) dt

$${Gamma}\:{function} \\ $$$$\Gamma\left({a}\right)=\int_{\mathrm{0}} ^{\infty} {t}^{{a}−\mathrm{1}} {e}^{−{t}} {dt} \\ $$

Commented by Abdoulaye last updated on 22/Feb/21

$${thank}\:{you}\:{very}\:{much} \\ $$

Commented by Abdoulaye last updated on 23/Feb/21

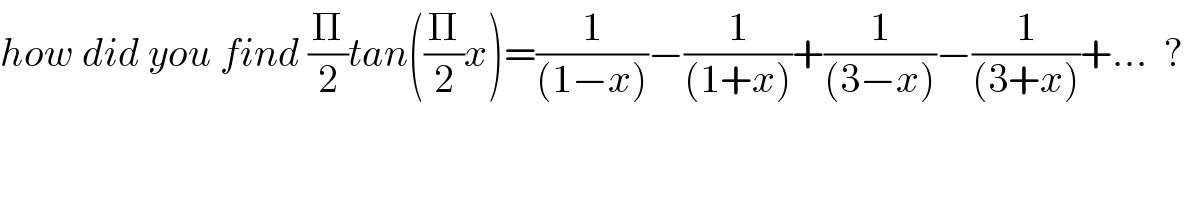
how did you find (Π/2)tan((Π/2)x)=(1/((1−x)))−(1/((1+x)))+(1/((3−x)))−(1/((3+x)))+... ?

$${how}\:{did}\:{you}\:{find}\:\frac{\Pi}{\mathrm{2}}{tan}\left(\frac{\Pi}{\mathrm{2}}{x}\right)=\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)}−\frac{\mathrm{1}}{\left(\mathrm{1}+{x}\right)}+\frac{\mathrm{1}}{\left(\mathrm{3}−{x}\right)}−\frac{\mathrm{1}}{\left(\mathrm{3}+{x}\right)}+…\:\:? \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply