Question Number 133664 by shaker last updated on 23/Feb/21
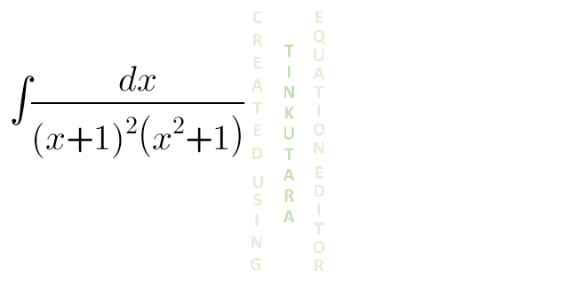
Answered by liberty last updated on 23/Feb/21
![partial fraction (1/((x+1)^2 (x^2 +1))) = (A/(x+1))+(B/((x+1)^2 ))+((Cx+D)/(x^2 +1)) ⇔ 1=(x+1)(x^2 +1)A+(x^2 +1)B+(x+1)^2 (Cx+D) x=0⇒1=A+B+D⇒A=−B...i x=−1⇒1=D...ii x=1⇒1=4A−2A+2(C+1) −1=2A+2C...iii x=−2⇒1=−5A−5A−2C+1 0 = −10A−2C; C=−5A...iv ⇒−1=−8A; A=(1/8); B=−(1/8) C= −(5/8) ; D= 1 I=∫[(1/(8(x+1))) −(1/(8(x+1)^2 )) +((−(5/8)x+1)/(x^2 +1)) ]dx =(1/8)ln ∣x+1∣+(1/(8(x+1)))−(5/8)∫ (x/(x^2 +1))dx +arctan (x) =((ln ∣x+1∣)/8) +(1/(8x+8))+arctan (x)−(5/(16)) ln ∣x^2 +1∣ + c](https://www.tinkutara.com/question/Q133665.png)
$$\mathrm{partial}\:\mathrm{fraction} \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)}\:=\:\frac{\mathrm{A}}{\mathrm{x}+\mathrm{1}}+\frac{\mathrm{B}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{Cx}+\mathrm{D}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\Leftrightarrow\:\mathrm{1}=\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\mathrm{A}+\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\mathrm{B}+\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{Cx}+\mathrm{D}\right) \\ $$$$\mathrm{x}=\mathrm{0}\Rightarrow\mathrm{1}=\mathrm{A}+\mathrm{B}+\mathrm{D}\Rightarrow\mathrm{A}=−\mathrm{B}…\mathrm{i} \\ $$$$\mathrm{x}=−\mathrm{1}\Rightarrow\mathrm{1}=\mathrm{D}…\mathrm{ii} \\ $$$$\mathrm{x}=\mathrm{1}\Rightarrow\mathrm{1}=\mathrm{4A}−\mathrm{2A}+\mathrm{2}\left(\mathrm{C}+\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:−\mathrm{1}=\mathrm{2A}+\mathrm{2C}…\mathrm{iii} \\ $$$$\mathrm{x}=−\mathrm{2}\Rightarrow\mathrm{1}=−\mathrm{5A}−\mathrm{5A}−\mathrm{2C}+\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\:=\:−\mathrm{10A}−\mathrm{2C};\:\mathrm{C}=−\mathrm{5A}…\mathrm{iv} \\ $$$$\Rightarrow−\mathrm{1}=−\mathrm{8A};\:\mathrm{A}=\frac{\mathrm{1}}{\mathrm{8}};\:\mathrm{B}=−\frac{\mathrm{1}}{\mathrm{8}} \\ $$$$\mathrm{C}=\:−\frac{\mathrm{5}}{\mathrm{8}}\:;\:\mathrm{D}=\:\mathrm{1} \\ $$$$\mathrm{I}=\int\left[\frac{\mathrm{1}}{\mathrm{8}\left(\mathrm{x}+\mathrm{1}\right)}\:−\frac{\mathrm{1}}{\mathrm{8}\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\:+\frac{−\frac{\mathrm{5}}{\mathrm{8}}\mathrm{x}+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\:\right]\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\mathrm{ln}\:\mid\mathrm{x}+\mathrm{1}\mid+\frac{\mathrm{1}}{\mathrm{8}\left(\mathrm{x}+\mathrm{1}\right)}−\frac{\mathrm{5}}{\mathrm{8}}\int\:\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx}\:+\mathrm{arctan}\:\left(\mathrm{x}\right) \\ $$$$=\frac{\mathrm{ln}\:\mid\mathrm{x}+\mathrm{1}\mid}{\mathrm{8}}\:+\frac{\mathrm{1}}{\mathrm{8x}+\mathrm{8}}+\mathrm{arctan}\:\left(\mathrm{x}\right)−\frac{\mathrm{5}}{\mathrm{16}}\:\mathrm{ln}\:\mid\mathrm{x}^{\mathrm{2}} +\mathrm{1}\mid\:+\:\mathrm{c} \\ $$$$ \\ $$
