Question-133757

Question Number 133757 by liberty last updated on 24/Feb/21

Answered by bobhans last updated on 24/Feb/21

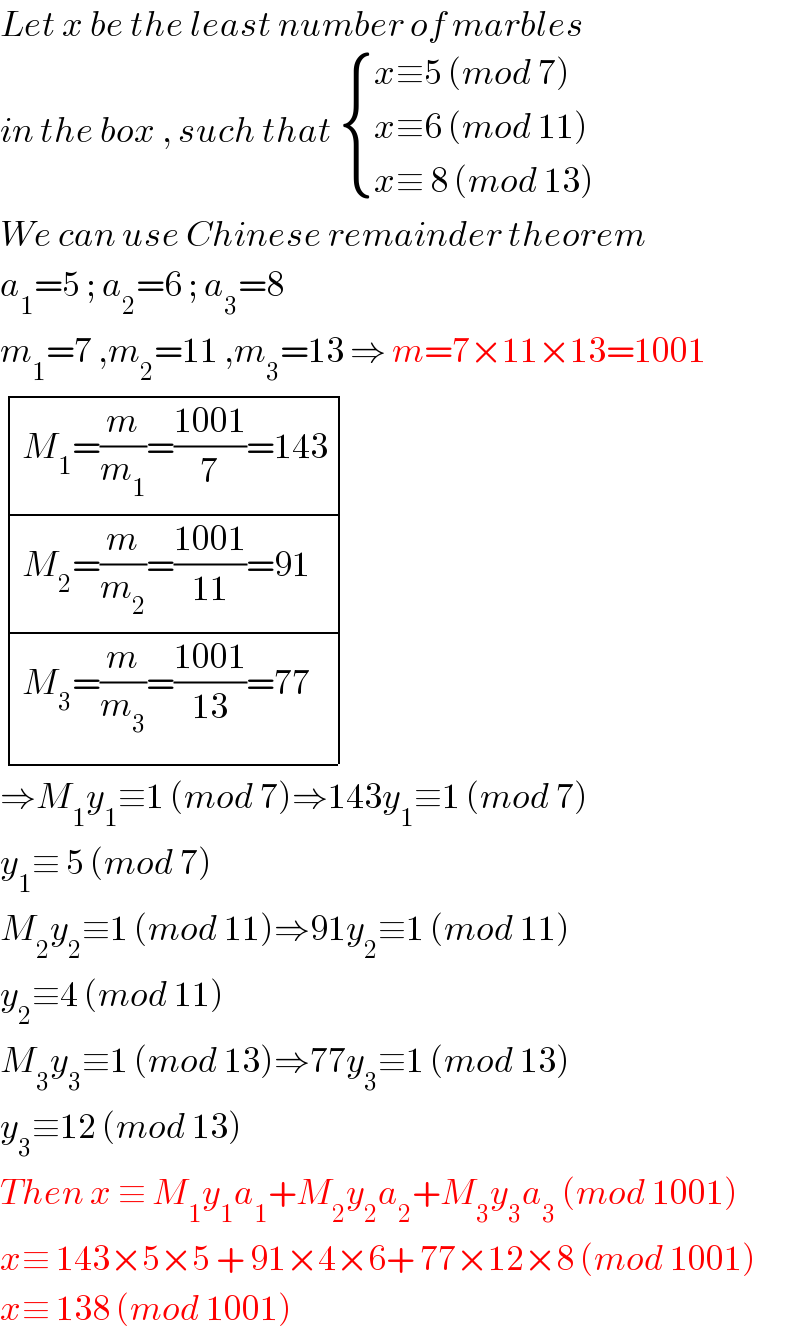
Let x be the least number of marbles in the box , such that { ((x≡5 (mod 7))),((x≡6 (mod 11))),((x≡ 8 (mod 13))) :} We can use Chinese remainder theorem a_1 =5 ; a_2 =6 ; a_3 =8 m_1 =7 ,m_2 =11 ,m_3 =13 ⇒ m=7×11×13=1001 determinant (((M_1 =(m/m_1 )=((1001)/7)=143)),((M_2 =(m/m_2 )=((1001)/(11))=91)),((M_3 =(m/m_3 )=((1001)/(13))=77))) ⇒M_1 y_1 ≡1 (mod 7)⇒143y_1 ≡1 (mod 7) y_1 ≡ 5 (mod 7) M_2 y_2 ≡1 (mod 11)⇒91y_2 ≡1 (mod 11) y_2 ≡4 (mod 11) M_3 y_3 ≡1 (mod 13)⇒77y_3 ≡1 (mod 13) y_3 ≡12 (mod 13) Then x ≡ M_1 y_1 a_1 +M_2 y_2 a_2 +M_3 y_3 a_3 (mod 1001) x≡ 143×5×5 + 91×4×6+ 77×12×8 (mod 1001) x≡ 138 (mod 1001)

$${Let}\:{x}\:{be}\:{the}\:{least}\:{number}\:{of}\:{marbles} \\ $$$${in}\:{the}\:{box}\:,\:{such}\:{that}\:\begin{cases}{{x}\equiv\mathrm{5}\:\left({mod}\:\mathrm{7}\right)}\\{{x}\equiv\mathrm{6}\:\left({mod}\:\mathrm{11}\right)}\\{{x}\equiv\:\mathrm{8}\:\left({mod}\:\mathrm{13}\right)}\end{cases} \\ $$$${We}\:{can}\:{use}\:{Chinese}\:{remainder}\:{theorem} \\ $$$${a}_{\mathrm{1}} =\mathrm{5}\:;\:{a}_{\mathrm{2}} =\mathrm{6}\:;\:{a}_{\mathrm{3}} =\mathrm{8} \\ $$$${m}_{\mathrm{1}} =\mathrm{7}\:,{m}_{\mathrm{2}} =\mathrm{11}\:,{m}_{\mathrm{3}} =\mathrm{13}\:\Rightarrow\:{m}=\mathrm{7}×\mathrm{11}×\mathrm{13}=\mathrm{1001} \\ $$$$\begin{array}{|c|c|c|}{{M}_{\mathrm{1}} =\frac{{m}}{{m}_{\mathrm{1}} }=\frac{\mathrm{1001}}{\mathrm{7}}=\mathrm{143}}\\{{M}_{\mathrm{2}} =\frac{{m}}{{m}_{\mathrm{2}} }=\frac{\mathrm{1001}}{\mathrm{11}}=\mathrm{91}}\\{{M}_{\mathrm{3}} =\frac{{m}}{{m}_{\mathrm{3}} }=\frac{\mathrm{1001}}{\mathrm{13}}=\mathrm{77}}\\\hline\end{array} \\ $$$$\Rightarrow{M}_{\mathrm{1}} {y}_{\mathrm{1}} \equiv\mathrm{1}\:\left({mod}\:\mathrm{7}\right)\Rightarrow\mathrm{143}{y}_{\mathrm{1}} \equiv\mathrm{1}\:\left({mod}\:\mathrm{7}\right) \\ $$$${y}_{\mathrm{1}} \equiv\:\mathrm{5}\:\left({mod}\:\mathrm{7}\right) \\ $$$${M}_{\mathrm{2}} {y}_{\mathrm{2}} \equiv\mathrm{1}\:\left({mod}\:\mathrm{11}\right)\Rightarrow\mathrm{91}{y}_{\mathrm{2}} \equiv\mathrm{1}\:\left({mod}\:\mathrm{11}\right) \\ $$$${y}_{\mathrm{2}} \equiv\mathrm{4}\:\left({mod}\:\mathrm{11}\right) \\ $$$${M}_{\mathrm{3}} {y}_{\mathrm{3}} \equiv\mathrm{1}\:\left({mod}\:\mathrm{13}\right)\Rightarrow\mathrm{77}{y}_{\mathrm{3}} \equiv\mathrm{1}\:\left({mod}\:\mathrm{13}\right) \\ $$$${y}_{\mathrm{3}} \equiv\mathrm{12}\:\left({mod}\:\mathrm{13}\right) \\ $$$${Then}\:{x}\:\equiv\:{M}_{\mathrm{1}} {y}_{\mathrm{1}} {a}_{\mathrm{1}} +{M}_{\mathrm{2}} {y}_{\mathrm{2}} {a}_{\mathrm{2}} +{M}_{\mathrm{3}} {y}_{\mathrm{3}} {a}_{\mathrm{3}} \:\left({mod}\:\mathrm{1001}\right) \\ $$$${x}\equiv\:\mathrm{143}×\mathrm{5}×\mathrm{5}\:+\:\mathrm{91}×\mathrm{4}×\mathrm{6}+\:\mathrm{77}×\mathrm{12}×\mathrm{8}\:\left({mod}\:\mathrm{1001}\right) \\ $$$${x}\equiv\:\mathrm{138}\:\left({mod}\:\mathrm{1001}\right) \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply