Menu Close

Question-133916

Tinku Tara 0 Comments
Pin




Question Number 133916 by shaker last updated on 25/Feb/21
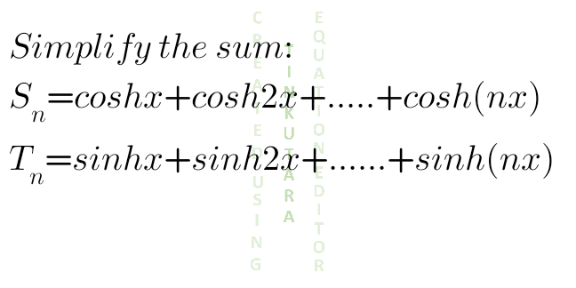
Answered by TheSupreme last updated on 25/Feb/21
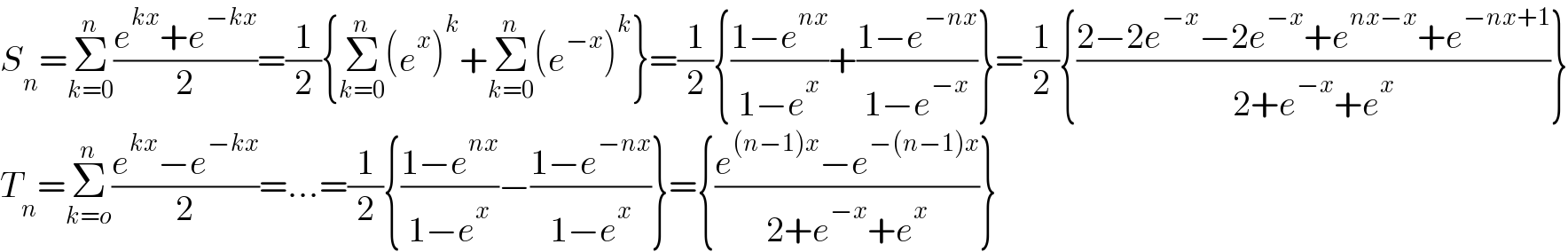
S_n =Σ_(k=0) ^n ((e^(kx) +e^(−kx) )/2)=(1/2){Σ_(k=0) ^n (e^x )^k +Σ_(k=0) ^n (e^(−x) )^k }=(1/2){((1−e^(nx) )/(1−e^x ))+((1−e^(−nx) )/(1−e^(−x) ))}=(1/2){((2−2e^(−x) −2e^(−x) +e^(nx−x) +e^(−nx+1) )/(2+e^(−x) +e^x ))} T_n =Σ_(k=o) ^n ((e^(kx) −e^(−kx) )/2)=...=(1/2){((1−e^(nx) )/(1−e^x ))−((1−e^(−nx) )/(1−e^x ))}={((e^((n−1)x) −e^(−(n−1)x) )/(2+e^(−x) +e^x ))}
$${S}_{{n}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{{e}^{{kx}} +{e}^{−{kx}} }{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}\left\{\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\left({e}^{{x}} \right)^{{k}} +\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\left({e}^{−{x}} \right)^{{k}} \right\}=\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{\mathrm{1}−{e}^{{nx}} }{\mathrm{1}−{e}^{{x}} }+\frac{\mathrm{1}−{e}^{−{nx}} }{\mathrm{1}−{e}^{−{x}} }\right\}=\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{\mathrm{2}−\mathrm{2}{e}^{−{x}} −\mathrm{2}{e}^{−{x}} +{e}^{{nx}−{x}} +{e}^{−{nx}+\mathrm{1}} }{\mathrm{2}+{e}^{−{x}} +{e}^{{x}} }\right\} \\ $$$${T}_{{n}} =\underset{{k}={o}} {\overset{{n}} {\sum}}\frac{{e}^{{kx}} −{e}^{−{kx}} }{\mathrm{2}}=…=\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{\mathrm{1}−{e}^{{nx}} }{\mathrm{1}−{e}^{{x}} }−\frac{\mathrm{1}−{e}^{−{nx}} }{\mathrm{1}−{e}^{{x}} }\right\}=\left\{\frac{{e}^{\left({n}−\mathrm{1}\right){x}} −{e}^{−\left({n}−\mathrm{1}\right){x}} }{\mathrm{2}+{e}^{−{x}} +{e}^{{x}} }\right\} \\ $$
Answered by antoineop last updated on 25/Feb/21
S_n = (1/2)[Σ_(k = 1) ^n e^(kx) +Σ_(k = 1) ^n e^(−kx) ] = (1/2)[e^x ((1−e^(nx) )/(1−e^x ))+e^(−x) ((1−e^(−nx) )/(1−e^(−x) ))] = (1/2)[(e^((n+2)x/2) /e^(x/2) )(((e^(−nx/2) −e^(nx/2) )/(e^(−x/2) −e^(x/2) )))+(e^(−(n+2)x/2) /e^(−x/2) )(((e^(nx/2) −e^(−nx/2) )/(e^(x/2) −e^(−x/2) )))] = (1/2)[e^((n+1)x/2) (((−2sinh(((nx)/2)))/(−2sinh((x/2)))))+e^(−(n+1)x/2) (((2sinh(((nx)/2)))/(2sinh((x/2)))))] S_n = cosh((((n+1)x)/2))((sinh(((nx)/2)))/(sinh ((x/2)))) T_n = sinh(((n+1)/2)x)((sinh(((nx)/2)))/(sinh((x/2))))
$${S}_{{n}} \:=\:\frac{\mathrm{1}}{\mathrm{2}}\left[\underset{{k}\:=\:\mathrm{1}} {\overset{{n}} {\sum}}{e}^{{kx}} \:\:\:+\underset{{k}\:=\:\mathrm{1}} {\overset{{n}} {\sum}}{e}^{−{kx}} \right]\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left[{e}^{{x}} \frac{\mathrm{1}−{e}^{{nx}} }{\mathrm{1}−{e}^{{x}} }+{e}^{−{x}} \frac{\mathrm{1}−{e}^{−{nx}} }{\mathrm{1}−{e}^{−{x}} }\right] \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{{e}^{\left({n}+\mathrm{2}\right){x}/\mathrm{2}} }{{e}^{{x}/\mathrm{2}} }\left(\frac{{e}^{−{nx}/\mathrm{2}} −{e}^{{nx}/\mathrm{2}} }{{e}^{−{x}/\mathrm{2}} −{e}^{{x}/\mathrm{2}} }\right)+\frac{{e}^{−\left({n}+\mathrm{2}\right){x}/\mathrm{2}} }{{e}^{−{x}/\mathrm{2}} }\left(\frac{{e}^{{nx}/\mathrm{2}} −{e}^{−{nx}/\mathrm{2}} }{{e}^{{x}/\mathrm{2}} −{e}^{−{x}/\mathrm{2}} }\right)\right] \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\left[{e}^{\left({n}+\mathrm{1}\right){x}/\mathrm{2}} \left(\frac{−\mathrm{2sinh}\left(\frac{{nx}}{\mathrm{2}}\right)}{−\mathrm{2sinh}\left(\frac{{x}}{\mathrm{2}}\right)}\right)+{e}^{−\left({n}+\mathrm{1}\right){x}/\mathrm{2}} \left(\frac{\mathrm{2sinh}\left(\frac{{nx}}{\mathrm{2}}\right)}{\mathrm{2sinh}\left(\frac{{x}}{\mathrm{2}}\right)}\right)\right] \\ $$$${S}_{{n}} \:=\:\mathrm{cosh}\left(\frac{\left({n}+\mathrm{1}\right){x}}{\mathrm{2}}\right)\frac{\mathrm{sinh}\left(\frac{{nx}}{\mathrm{2}}\right)}{\mathrm{sinh}\:\left(\frac{{x}}{\mathrm{2}}\right)} \\ $$$${T}_{{n}} \:=\:\mathrm{sinh}\left(\frac{{n}+\mathrm{1}}{\mathrm{2}}{x}\right)\frac{\mathrm{sinh}\left(\frac{{nx}}{\mathrm{2}}\right)}{\mathrm{sinh}\left(\frac{{x}}{\mathrm{2}}\right)} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *