Menu Close

Question-134704

Tinku Tara 0 Comments
Pin




Question Number 134704 by I want to learn more last updated on 06/Mar/21
Answered by mr W last updated on 07/Mar/21
Commented by mr W last updated on 07/Mar/21
(a) R=resultant from F_1 ,F_2 ,F_3 R_x =6+9×cos 45°=6+(9/( (√2)))=((12+9(√2))/2) R_y =12+9×sin 45°=12+(9/( (√2)))=((24+9(√2))/2) R=(√(R_x ^2 +R_y ^2 ))=((√((12+9(√2))^2 +(24+9(√2))^2 ))/2) =3(√(29+18(√2)))≈22.138 units tan θ=(R_y /R_x )=((24+9(√2))/(12+9(√2)))=6(√2)−7 ⇒θ=tan^(−1) (6(√2)−7)≈56.05° θ=angle between R and x−axis (b) tan α=(1/2)⇒sin α=(1/( (√5))), cos α=(2/( (√5))) F_4 cos α+F_5 sin α+R_x =0 (2F_4 +F_5 )(1/( (√5)))+((12+9(√2))/2)=0 ⇒2F_4 +F_5 =−(((√5)(12+9(√2)))/2) ...(i) F_4 sin α+F_5 cos α+R_y =0 (F_4 +2F_5 )(1/( (√5)))+((24+9(√2))/2)=0 ⇒F_4 +2F_5 =−(((√5)(24+9(√2)))/2) ...(ii) 2(i)−(ii): 3F_4 =−2×(((√5)(12+9(√2)))/2)+(((√5)(24+9(√2)))/2) ⇒F_4 =−((3(√(10)))/2)≈−4.74 units 2(ii)−(i): 3F_5 =−2×(((√5)(24+9(√2)))/2)+(((√5)(12+9(√2)))/2) ⇒F_5 =−(((12+3(√2))(√5))/2)≈−18.16 units F_4 and F_5 are in opposite direction as shown.
$$\left({a}\right) \\ $$$${R}={resultant}\:{from}\:{F}_{\mathrm{1}} ,{F}_{\mathrm{2}} ,{F}_{\mathrm{3}} \\ $$$${R}_{{x}} =\mathrm{6}+\mathrm{9}×\mathrm{cos}\:\mathrm{45}°=\mathrm{6}+\frac{\mathrm{9}}{\:\sqrt{\mathrm{2}}}=\frac{\mathrm{12}+\mathrm{9}\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$${R}_{{y}} =\mathrm{12}+\mathrm{9}×\mathrm{sin}\:\mathrm{45}°=\mathrm{12}+\frac{\mathrm{9}}{\:\sqrt{\mathrm{2}}}=\frac{\mathrm{24}+\mathrm{9}\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$${R}=\sqrt{{R}_{{x}} ^{\mathrm{2}} +{R}_{{y}} ^{\mathrm{2}} }=\frac{\sqrt{\left(\mathrm{12}+\mathrm{9}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} +\left(\mathrm{24}+\mathrm{9}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }}{\mathrm{2}} \\ $$$$=\mathrm{3}\sqrt{\mathrm{29}+\mathrm{18}\sqrt{\mathrm{2}}}\approx\mathrm{22}.\mathrm{138}\:{units} \\ $$$$\mathrm{tan}\:\theta=\frac{{R}_{{y}} }{{R}_{{x}} }=\frac{\mathrm{24}+\mathrm{9}\sqrt{\mathrm{2}}}{\mathrm{12}+\mathrm{9}\sqrt{\mathrm{2}}}=\mathrm{6}\sqrt{\mathrm{2}}−\mathrm{7} \\ $$$$\Rightarrow\theta=\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{6}\sqrt{\mathrm{2}}−\mathrm{7}\right)\approx\mathrm{56}.\mathrm{05}° \\ $$$$\theta={angle}\:{between}\:{R}\:{and}\:{x}−{axis} \\ $$$$ \\ $$$$\left({b}\right) \\ $$$$\mathrm{tan}\:\alpha=\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\mathrm{sin}\:\alpha=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}},\:\mathrm{cos}\:\alpha=\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}} \\ $$$${F}_{\mathrm{4}} \mathrm{cos}\:\alpha+{F}_{\mathrm{5}} \mathrm{sin}\:\alpha+{R}_{{x}} =\mathrm{0} \\ $$$$\left(\mathrm{2}{F}_{\mathrm{4}} +{F}_{\mathrm{5}} \right)\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}+\frac{\mathrm{12}+\mathrm{9}\sqrt{\mathrm{2}}}{\mathrm{2}}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}{F}_{\mathrm{4}} +{F}_{\mathrm{5}} =−\frac{\sqrt{\mathrm{5}}\left(\mathrm{12}+\mathrm{9}\sqrt{\mathrm{2}}\right)}{\mathrm{2}}\:\:\:…\left({i}\right) \\ $$$${F}_{\mathrm{4}} \mathrm{sin}\:\alpha+{F}_{\mathrm{5}} \mathrm{cos}\:\alpha+{R}_{{y}} =\mathrm{0} \\ $$$$\left({F}_{\mathrm{4}} +\mathrm{2}{F}_{\mathrm{5}} \right)\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}+\frac{\mathrm{24}+\mathrm{9}\sqrt{\mathrm{2}}}{\mathrm{2}}=\mathrm{0} \\ $$$$\Rightarrow{F}_{\mathrm{4}} +\mathrm{2}{F}_{\mathrm{5}} =−\frac{\sqrt{\mathrm{5}}\left(\mathrm{24}+\mathrm{9}\sqrt{\mathrm{2}}\right)}{\mathrm{2}}\:\:\:…\left({ii}\right) \\ $$$$\mathrm{2}\left({i}\right)−\left({ii}\right): \\ $$$$\mathrm{3}{F}_{\mathrm{4}} =−\mathrm{2}×\frac{\sqrt{\mathrm{5}}\left(\mathrm{12}+\mathrm{9}\sqrt{\mathrm{2}}\right)}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}}\left(\mathrm{24}+\mathrm{9}\sqrt{\mathrm{2}}\right)}{\mathrm{2}} \\ $$$$\Rightarrow{F}_{\mathrm{4}} =−\frac{\mathrm{3}\sqrt{\mathrm{10}}}{\mathrm{2}}\approx−\mathrm{4}.\mathrm{74}\:{units} \\ $$$$\mathrm{2}\left({ii}\right)−\left({i}\right): \\ $$$$\mathrm{3}{F}_{\mathrm{5}} =−\mathrm{2}×\frac{\sqrt{\mathrm{5}}\left(\mathrm{24}+\mathrm{9}\sqrt{\mathrm{2}}\right)}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}}\left(\mathrm{12}+\mathrm{9}\sqrt{\mathrm{2}}\right)}{\mathrm{2}} \\ $$$$\Rightarrow{F}_{\mathrm{5}} =−\frac{\left(\mathrm{12}+\mathrm{3}\sqrt{\mathrm{2}}\right)\sqrt{\mathrm{5}}}{\mathrm{2}}\approx−\mathrm{18}.\mathrm{16}\:{units} \\ $$$${F}_{\mathrm{4}} \:{and}\:{F}_{\mathrm{5}} \:{are}\:{in}\:{opposite}\:{direction} \\ $$$${as}\:{shown}. \\ $$
Commented by I want to learn more last updated on 07/Mar/21
Wow, thanks sir, i really appreciate. God bless you sir.
$$\mathrm{Wow},\:\mathrm{thanks}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by I want to learn more last updated on 11/Mar/21
Thanks sir, i understand very well now.
$$\mathrm{Thanks}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{understand}\:\mathrm{very}\:\mathrm{well}\:\mathrm{now}. \\ $$
Commented by I want to learn more last updated on 11/Mar/21
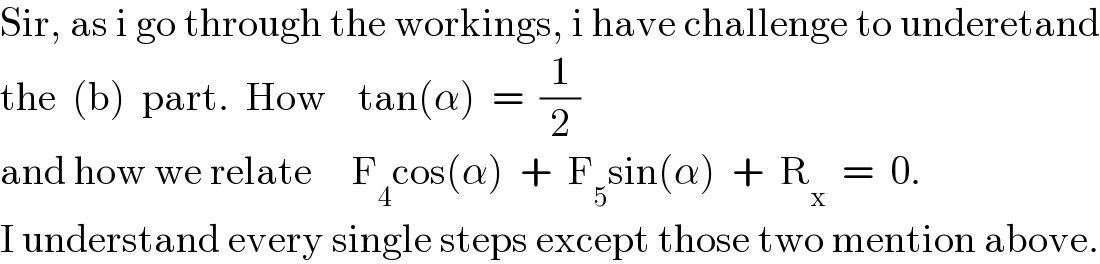
Sir, as i go through the workings, i have challenge to underetand the (b) part. How tan(α) = (1/2) and how we relate F_4 cos(α) + F_5 sin(α) + R_x = 0. I understand every single steps except those two mention above.
$$\mathrm{Sir},\:\mathrm{as}\:\mathrm{i}\:\mathrm{go}\:\mathrm{through}\:\mathrm{the}\:\mathrm{workings},\:\mathrm{i}\:\mathrm{have}\:\mathrm{challenge}\:\mathrm{to}\:\mathrm{underetand} \\ $$$$\mathrm{the}\:\:\left(\mathrm{b}\right)\:\:\mathrm{part}.\:\:\mathrm{How}\:\:\:\:\mathrm{tan}\left(\alpha\right)\:\:=\:\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{and}\:\mathrm{how}\:\mathrm{we}\:\mathrm{relate}\:\:\:\:\:\mathrm{F}_{\mathrm{4}} \mathrm{cos}\left(\alpha\right)\:\:+\:\:\mathrm{F}_{\mathrm{5}} \mathrm{sin}\left(\alpha\right)\:\:+\:\:\mathrm{R}_{\mathrm{x}} \:\:=\:\:\mathrm{0}. \\ $$$$\mathrm{I}\:\mathrm{understand}\:\mathrm{every}\:\mathrm{single}\:\mathrm{steps}\:\mathrm{except}\:\mathrm{those}\:\mathrm{two}\:\mathrm{mention}\:\mathrm{above}. \\ $$
Commented by mr W last updated on 11/Mar/21
H is midpoint of BC as given, ⇒BH=((BC)/2)=((AB)/2) tan α=((BH)/(AB))=(1/2)
$${H}\:{is}\:{midpoint}\:{of}\:{BC}\:{as}\:{given}, \\ $$$$\Rightarrow{BH}=\frac{{BC}}{\mathrm{2}}=\frac{{AB}}{\mathrm{2}} \\ $$$$\mathrm{tan}\:\alpha=\frac{{BH}}{{AB}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by mr W last updated on 11/Mar/21
here R_x =F_(1x) +F_(2x) +F_(3x) from part (a) F_(4x) =F_4 cos α F_(5x) =F_5 sin α in equilibrium ΣF_x =F_(1x) +F_(2x) +F_(3x) +F_(4x) +F_(5x) =0 ⇒F_4 cos(α) + F_5 sin(α) + R_x = 0
$${here}\:{R}_{{x}} ={F}_{\mathrm{1}{x}} +{F}_{\mathrm{2}{x}} +{F}_{\mathrm{3}{x}} \:{from}\:{part}\:\left({a}\right) \\ $$$${F}_{\mathrm{4}{x}} ={F}_{\mathrm{4}} \mathrm{cos}\:\alpha \\ $$$${F}_{\mathrm{5}{x}} ={F}_{\mathrm{5}} \mathrm{sin}\:\alpha \\ $$$${in}\:{equilibrium} \\ $$$$\Sigma{F}_{{x}} ={F}_{\mathrm{1}{x}} +{F}_{\mathrm{2}{x}} +{F}_{\mathrm{3}{x}} +{F}_{\mathrm{4}{x}} +{F}_{\mathrm{5}{x}} =\mathrm{0} \\ $$$$\Rightarrow\mathrm{F}_{\mathrm{4}} \mathrm{cos}\left(\alpha\right)\:\:+\:\:\mathrm{F}_{\mathrm{5}} \mathrm{sin}\left(\alpha\right)\:\:+\:\:\mathrm{R}_{\mathrm{x}} \:\:=\:\:\mathrm{0} \\ $$
Commented by I want to learn more last updated on 11/Mar/21
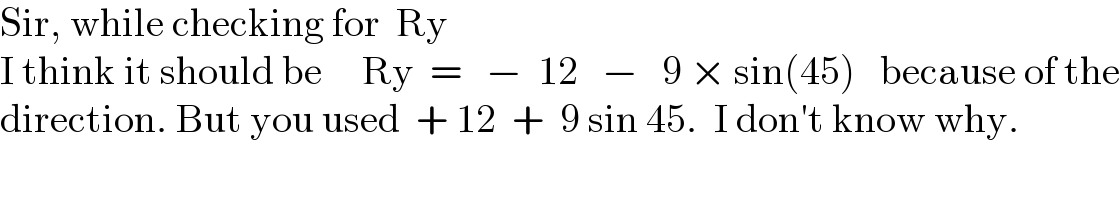
Sir, while checking for Ry I think it should be Ry = − 12 − 9 × sin(45) because of the direction. But you used + 12 + 9 sin 45. I don′t know why.
$$\mathrm{Sir},\:\mathrm{while}\:\mathrm{checking}\:\mathrm{for}\:\:\mathrm{Ry} \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{it}\:\mathrm{should}\:\mathrm{be}\:\:\:\:\:\mathrm{Ry}\:\:=\:\:\:−\:\:\mathrm{12}\:\:\:−\:\:\:\mathrm{9}\:×\:\mathrm{sin}\left(\mathrm{45}\right)\:\:\:\mathrm{because}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{direction}.\:\mathrm{But}\:\mathrm{you}\:\mathrm{used}\:\:+\:\mathrm{12}\:\:+\:\:\mathrm{9}\:\mathrm{sin}\:\mathrm{45}.\:\:\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{why}. \\ $$
Commented by I want to learn more last updated on 11/Mar/21
Commented by mr W last updated on 11/Mar/21
you can see in my diagram which x− and y−axis i used! if you like, it is the same as:
$${you}\:{can}\:{see}\:{in}\:{my}\:{diagram}\:{which}\:{x}− \\ $$$${and}\:{y}−{axis}\:{i}\:{used}! \\ $$$${if}\:{you}\:{like},\:{it}\:{is}\:{the}\:{same}\:{as}: \\ $$
Commented by mr W last updated on 11/Mar/21
Commented by mr W last updated on 11/Mar/21
now you say R_y =12+9 sin 45° is ok, though actually i changed nothing.
$${now}\:{you}\:{say}\:{R}_{{y}} =\mathrm{12}+\mathrm{9}\:\mathrm{sin}\:\mathrm{45}°\:{is}\:{ok}, \\ $$$${though}\:{actually}\:\:{i}\:{changed}\:{nothing}. \\ $$
Commented by I want to learn more last updated on 11/Mar/21
Thanks for clarification sir. I appreciate.
$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{clarification}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *