Question-134719

Question Number 134719 by 0731619177 last updated on 06/Mar/21

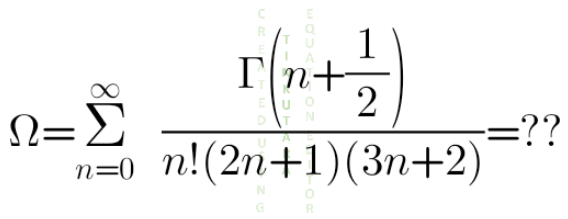
Commented by Dwaipayan Shikari last updated on 06/Mar/21

π^(3/2) −((3π)/2).((Γ((5/3)))/(Γ((7/6))))

$$\pi^{\frac{\mathrm{3}}{\mathrm{2}}} −\frac{\mathrm{3}\pi}{\mathrm{2}}.\frac{\Gamma\left(\frac{\mathrm{5}}{\mathrm{3}}\right)}{\Gamma\left(\frac{\mathrm{7}}{\mathrm{6}}\right)} \\ $$

Answered by CutieJanab last updated on 06/Mar/21

$${please}\:{solve}\:{tbis} \\ $$

Answered by Dwaipayan Shikari last updated on 06/Mar/21

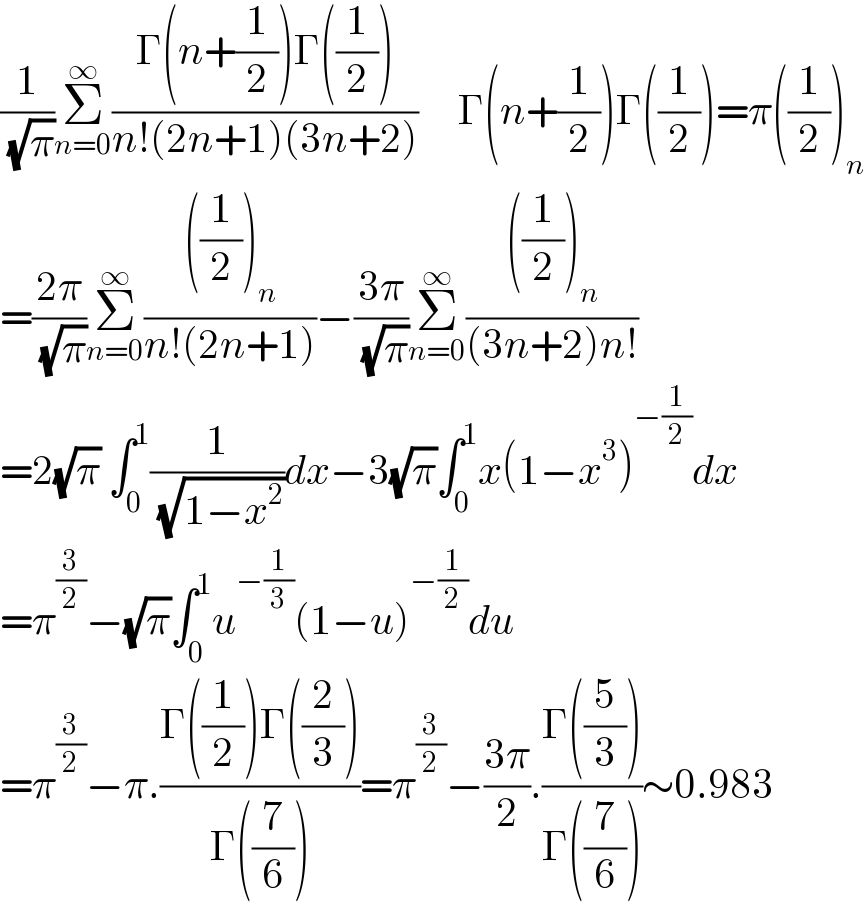
(1/( (√π)))Σ_(n=0) ^∞ ((Γ(n+(1/2))Γ((1/2)))/(n!(2n+1)(3n+2))) Γ(n+(1/2))Γ((1/2))=π((1/2))_n =((2π)/( (√π)))Σ_(n=0) ^∞ ((((1/2))_n )/(n!(2n+1)))−((3π)/( (√π)))Σ_(n=0) ^∞ ((((1/2))_n )/((3n+2)n!)) =2(√π) ∫_0 ^1 (1/( (√(1−x^2 ))))dx−3(√π)∫_0 ^1 x(1−x^3 )^(−(1/2)) dx =π^(3/2) −(√π)∫_0 ^1 u^(−(1/3)) (1−u)^(−(1/2)) du =π^(3/2) −π.((Γ((1/2))Γ((2/3)))/(Γ((7/6))))=π^(3/2) −((3π)/2).((Γ((5/3)))/(Γ((7/6))))∼0.983

$$\frac{\mathrm{1}}{\:\sqrt{\pi}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\Gamma\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{{n}!\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\mathrm{3}{n}+\mathrm{2}\right)}\:\:\:\:\:\Gamma\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\pi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)_{{n}} \\ $$$$=\frac{\mathrm{2}\pi}{\:\sqrt{\pi}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)_{{n}} }{{n}!\left(\mathrm{2}{n}+\mathrm{1}\right)}−\frac{\mathrm{3}\pi}{\:\sqrt{\pi}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)_{{n}} }{\left(\mathrm{3}{n}+\mathrm{2}\right){n}!}\:\:\: \\ $$$$=\mathrm{2}\sqrt{\pi}\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}−\mathrm{3}\sqrt{\pi}\int_{\mathrm{0}} ^{\mathrm{1}} {x}\left(\mathrm{1}−{x}^{\mathrm{3}} \right)^{−\frac{\mathrm{1}}{\mathrm{2}}} {dx} \\ $$$$=\pi^{\frac{\mathrm{3}}{\mathrm{2}}} −\sqrt{\pi}\int_{\mathrm{0}} ^{\mathrm{1}} {u}^{−\frac{\mathrm{1}}{\mathrm{3}}} \left(\mathrm{1}−{u}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} {du} \\ $$$$=\pi^{\frac{\mathrm{3}}{\mathrm{2}}} −\pi.\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{2}}{\mathrm{3}}\right)}{\Gamma\left(\frac{\mathrm{7}}{\mathrm{6}}\right)}=\pi^{\frac{\mathrm{3}}{\mathrm{2}}} −\frac{\mathrm{3}\pi}{\mathrm{2}}.\frac{\Gamma\left(\frac{\mathrm{5}}{\mathrm{3}}\right)}{\Gamma\left(\frac{\mathrm{7}}{\mathrm{6}}\right)}\sim\mathrm{0}.\mathrm{983} \\ $$

Commented by 0731619177 last updated on 06/Mar/21

$${answer}\:{is}\:{wrong}\: \\ $$

Commented by 0731619177 last updated on 06/Mar/21

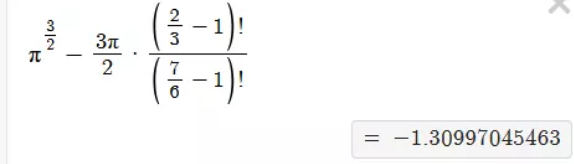
Commented by 0731619177 last updated on 06/Mar/21

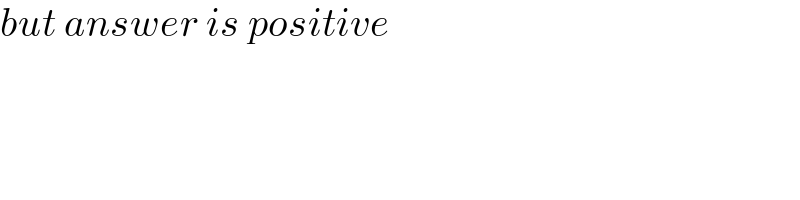
$${but}\:{answer}\:{is}\:{positive} \\ $$

Commented by Dwaipayan Shikari last updated on 06/Mar/21

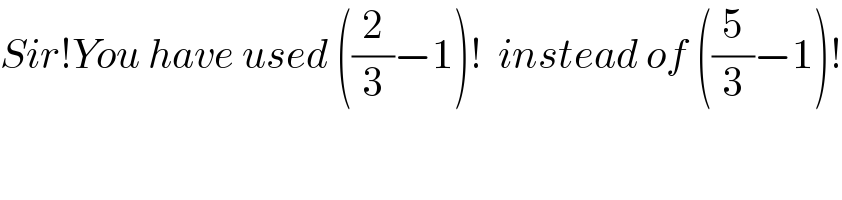
Sir!You have used ((2/3)−1)! instead of ((5/3)−1)!

$${Sir}!{You}\:{have}\:{used}\:\left(\frac{\mathrm{2}}{\mathrm{3}}−\mathrm{1}\right)!\:\:{instead}\:{of}\:\left(\frac{\mathrm{5}}{\mathrm{3}}−\mathrm{1}\right)! \\ $$

Commented by Dwaipayan Shikari last updated on 06/Mar/21

$${Hahhahah}..\:{Sir}\:{Power}\:{again}.. \\ $$😛

Facebook Tweet Pin

Leave a Reply Cancel reply