Question Number 134948 by rexford last updated on 08/Mar/21

Commented by bobhans last updated on 09/Mar/21
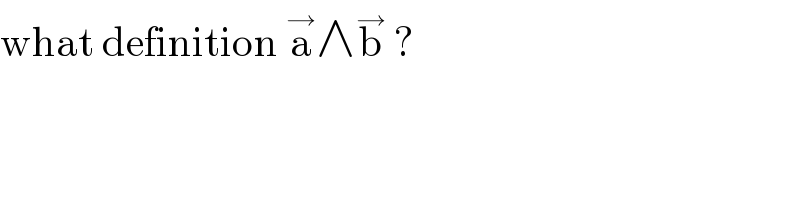
$$\mathrm{what}\:\mathrm{definition}\:\overset{\rightarrow} {\mathrm{a}}\wedge\overset{\rightarrow} {\mathrm{b}}\:? \\ $$
Commented by rexford last updated on 09/Mar/21

$${cross}\:{product} \\ $$
Answered by bramlexs22 last updated on 09/Mar/21
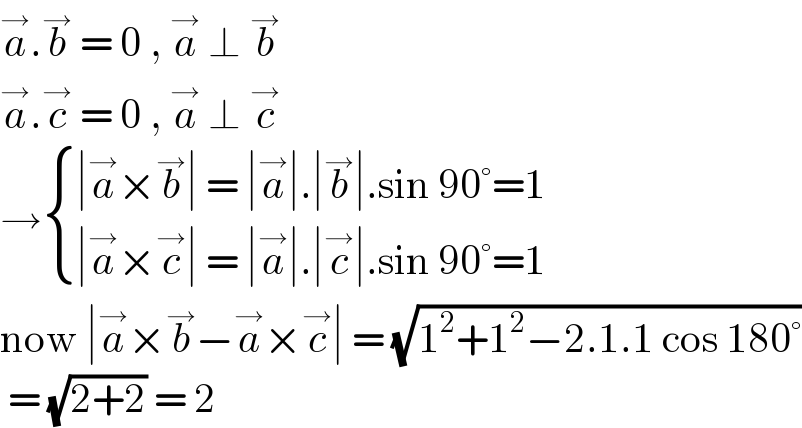
$$\overset{\rightarrow} {{a}}.\overset{\rightarrow} {{b}}\:=\:\mathrm{0}\:,\:\overset{\rightarrow} {{a}}\:\bot\:\overset{\rightarrow} {{b}} \\ $$$$\overset{\rightarrow} {{a}}.\overset{\rightarrow} {{c}}\:=\:\mathrm{0}\:,\:\overset{\rightarrow} {{a}}\:\bot\:\overset{\rightarrow} {{c}} \\ $$$$\rightarrow\begin{cases}{\mid\overset{\rightarrow} {{a}}×\overset{\rightarrow} {{b}}\mid\:=\:\mid\overset{\rightarrow} {{a}}\mid.\mid\overset{\rightarrow} {{b}}\mid.\mathrm{sin}\:\mathrm{90}°=\mathrm{1}}\\{\mid\overset{\rightarrow} {{a}}×\overset{\rightarrow} {{c}}\mid\:=\:\mid\overset{\rightarrow} {{a}}\mid.\mid\overset{\rightarrow} {{c}}\mid.\mathrm{sin}\:\mathrm{90}°=\mathrm{1}}\end{cases} \\ $$$$\mathrm{now}\:\mid\overset{\rightarrow} {{a}}×\overset{\rightarrow} {{b}}−\overset{\rightarrow} {{a}}×\overset{\rightarrow} {{c}}\mid\:=\:\sqrt{\mathrm{1}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} −\mathrm{2}.\mathrm{1}.\mathrm{1}\:\mathrm{cos}\:\mathrm{180}°} \\ $$$$\:=\:\sqrt{\mathrm{2}+\mathrm{2}}\:=\:\mathrm{2} \\ $$
