Question Number 135054 by rexford last updated on 09/Mar/21

Commented by mr W last updated on 10/Mar/21

$${there}\:{are}\:{three}\:{possible}\:{answers}: \\ $$$${in}\:{plane}:\:\mid{a}\mid=\frac{\sqrt{\mathrm{6}}}{\mathrm{2}} \\ $$$${in}\:{space}:\:\mid{a}\mid=\mathrm{1}\:{or}\:\sqrt{\mathrm{3}} \\ $$
Commented by liberty last updated on 10/Mar/21

$$\mathrm{i}\:\mathrm{think}\:\mathrm{this}\:\mathrm{question}\:\mathrm{wrong}\:\mathrm{sir} \\ $$
Commented by mr W last updated on 10/Mar/21

$${why}\:{wrong}? \\ $$
Answered by EDWIN88 last updated on 09/Mar/21

$$\mid\overset{\rightarrow} {{a}}+\overset{\rightarrow} {{b}}+\overset{\rightarrow} {{c}}\mid=\sqrt{\mid\overset{\rightarrow} {{a}}\mid^{\mathrm{2}} +\mid\overset{\rightarrow} {{b}}\mid^{\mathrm{2}} +\mid\overset{\rightarrow} {{c}}\mid^{\mathrm{2}} −\mathrm{2}\left(\mid\overset{\rightarrow} {{a}}\mid\mid\overset{\rightarrow} {{b}}\mid.\mathrm{cos}\:\frac{\pi}{\mathrm{3}}+\mid\overset{\rightarrow} {{a}}\mid\mid\overset{\rightarrow} {{c}}\mid.\mathrm{cos}\:\frac{\pi}{\mathrm{3}}+\mid\overset{\rightarrow} {{b}}\mid\mid\overset{\rightarrow} {{c}}\mid.\mathrm{cos}\:\frac{\pi}{\mathrm{3}}\right)} \\ $$$$ \\ $$
Answered by mr W last updated on 10/Mar/21

$${this}\:{question}\:{may}\:{have}\:{more}\:{than} \\ $$$${one}\:{solution}. \\ $$$$ \\ $$$${in}\:\mathrm{3}\boldsymbol{{D}}\:\boldsymbol{{space}}\:{there}\:{are}\:{basically}\:{two} \\ $$$${cases}. \\ $$$$\boldsymbol{{case}}\:\mathrm{1}:\:{all}\:{three}\:{vectors}\:{are}\:{in}\:“{same}“ \\ $$$${direction} \\ $$
Commented by mr W last updated on 10/Mar/21

Commented by mr W last updated on 10/Mar/21

$${in}\:{this}\:{case}: \\ $$$$\mid{a}+{b}+{c}\mid=\mathrm{3}\sqrt{\mathrm{1}^{\mathrm{2}} −\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\right)^{\mathrm{2}} }\mid{a}\mid=\sqrt{\mathrm{6}}\mid{a}\mid=\sqrt{\mathrm{6}} \\ $$$$\Rightarrow\mid{a}\mid=\mathrm{1} \\ $$$$ \\ $$$$\boldsymbol{{case}}\:\mathrm{2}:\:{two}\:{vectors}\:{are}\:{in}\:{the}\:“{same}'' \\ $$$${direction},\:{the}\:{third}\:{one}\:{in}\:“{opposite}'' \\ $$$${direction}. \\ $$
Commented by mr W last updated on 10/Mar/21

Commented by mr W last updated on 10/Mar/21

$${in}\:{this}\:{case}, \\ $$$$\mid{a}+{b}+{c}\mid=\sqrt{\mathrm{1}^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} +\left(\sqrt{\frac{\mathrm{2}}{\mathrm{3}}}\right)^{\mathrm{2}} }\mid{a}\mid=\sqrt{\mathrm{6}} \\ $$$$\Rightarrow\mid{a}\mid=\sqrt{\mathrm{3}} \\ $$
Commented by mr W last updated on 10/Mar/21

$${in}\:\mathrm{2}\boldsymbol{{D}}\:\boldsymbol{{plane}}\:{there}\:{are}\:{basically}\:{two} \\ $$$${cases}. \\ $$$$\boldsymbol{{case}}\:\mathrm{1}:\:{all}\:{three}\:{vectors}\:{are}\:{in}\:{the} \\ $$$${same}\:“{direction}'',\:{clockwise}\:{or} \\ $$$${counterclockwise}. \\ $$
Commented by mr W last updated on 10/Mar/21

Commented by mr W last updated on 10/Mar/21

$${in}\:{this}\:{case}:\:\boldsymbol{{a}}+\boldsymbol{{b}}+\boldsymbol{{c}}=\mathrm{0} \\ $$$${but}\:{since}\:\mid{a}+{b}+{c}\mid=\sqrt{\mathrm{6}},\:{so}\:{this}\:{case} \\ $$$${is}\:{not}\:{possible}. \\ $$$$ \\ $$$$\boldsymbol{{case}}\:\mathrm{2}:\:{two}\:{vectors}\:{are}\:{in}\:{the}\:{same} \\ $$$$“{direction}''\:{and}\:{the}\:{third}\:{one}\:{is}\:{in} \\ $$$$“{opposite}\:{direction}''. \\ $$
Commented by mr W last updated on 10/Mar/21

Commented by mr W last updated on 10/Mar/21
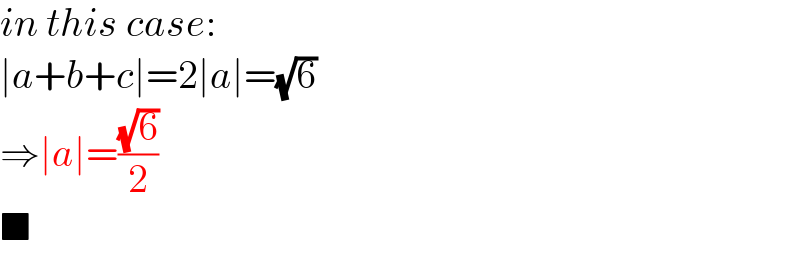
$${in}\:{this}\:{case}: \\ $$$$\mid{a}+{b}+{c}\mid=\mathrm{2}\mid{a}\mid=\sqrt{\mathrm{6}} \\ $$$$\Rightarrow\mid{a}\mid=\frac{\sqrt{\mathrm{6}}}{\mathrm{2}} \\ $$$$\blacksquare \\ $$
Commented by bramlexs22 last updated on 10/Mar/21

$$ \\ $$the definition of the angle of two vectors is that the vector must meet the starting point with the base or the end point with the end point
Commented by bramlexs22 last updated on 10/Mar/21
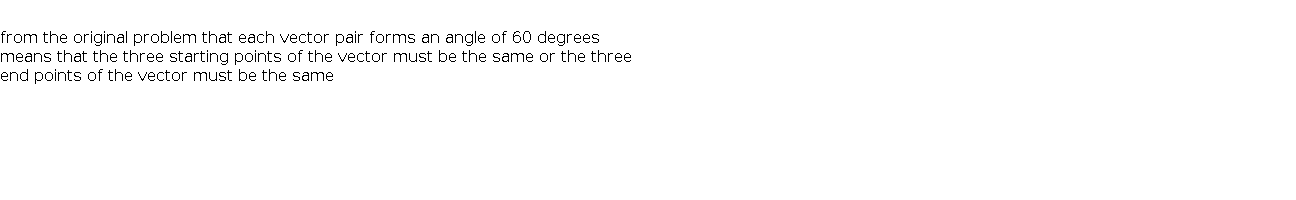
$$ \\ $$from the original problem that each vector pair forms an angle of 60 degrees means that the three starting points of the vector must be the same or the three end points of the vector must be the same
Commented by mr W last updated on 10/Mar/21

$${a}\:{vector}\:{has}\:\boldsymbol{{NO}}\:{fixed}\:{starting}\:{point} \\ $$$${or}\:{ending}\:{point}! \\ $$$${or}\:{can}\:{you}\:{tell}\:{me}\:{where}\:{the}\:{starting} \\ $$$${point}\:{and}\:{the}\:{ending}\:{point}\:{from}\:{the} \\ $$$${vector}\:\overset{\rightarrow} {\boldsymbol{{a}}}=\boldsymbol{{i}}+\mathrm{2}\boldsymbol{{j}}+\mathrm{3}\boldsymbol{{k}}\:{are}?\:{and}\:{where} \\ $$$${the}\:{vectors}\:\overset{\rightarrow} {\boldsymbol{{a}}}=\boldsymbol{{i}}+\mathrm{2}\boldsymbol{{j}}+\mathrm{3}\boldsymbol{{k}}\:{and} \\ $$$$\overset{\rightarrow} {\boldsymbol{{b}}}=−\boldsymbol{{i}}+\mathrm{3}\boldsymbol{{j}}+\mathrm{2}\boldsymbol{{k}}\:{meet}? \\ $$
Commented by bramlexs22 last updated on 10/Mar/21

$$ \\ $$we need to shift one of the vectors or take another vector parallel to it so that they meet at the same starting point
Commented by bramlexs22 last updated on 10/Mar/21

Commented by mr W last updated on 10/Mar/21

$${i}\:{know}. \\ $$$${i}\:{used}\:“{two}\:{vectors}\:{make}\:{an}\:{angle}\:\theta'', \\ $$$${that}\:{means}\:{they}\:{make}\:{also}\:{an}\:{angle} \\ $$$$\pi−\theta. \\ $$$${if}\:{exactly}\:{following}\:{the}\:{definition}\:{of} \\ $$$${angle}\:{between}\:{two}\:{vectors},\:{then}\:{there} \\ $$$${is}\:{only}\:{the}\:{case}\:\mathrm{1}\:{in}\:\mathrm{3}{D}\:{space}\:{which} \\ $$$${satisfies}\:{the}\:{question}.\:{in}\:{a}\:{plane}\:{you} \\ $$$${can}\:{not}\:{find}\:{three}\:{vectors}\:{with}\:{equal} \\ $$$${magnitude}\:{and}\:{the}\:{angle}\:{between} \\ $$$${two}\:{of}\:{them}\:{is}\:\mathrm{60}°. \\ $$
Commented by mr W last updated on 10/Mar/21

Commented by mr W last updated on 10/Mar/21

$${following}\:{definition}\:{the}\:{angle} \\ $$$${between}\:\boldsymbol{{a}}\:{and}\:\boldsymbol{{b}}\:{is}\:\theta,\:{and}\:{only}\:\theta. \\ $$
Commented by bramlexs22 last updated on 10/Mar/21
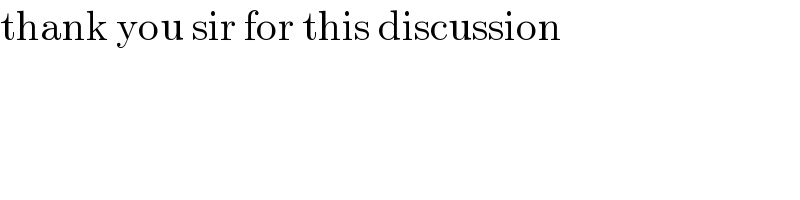
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}\:\mathrm{for}\:\mathrm{this}\:\mathrm{discussion} \\ $$
Commented by rexford last updated on 10/Mar/21

$${The}\:{answer}\:{is}\:\mathrm{1} \\ $$$${but}\:{i}\:{still}\:{don}'{t}\:{get}\:{the}\:{approach}\:{u}\:{used}. \\ $$$${please},{can}\:{u}\:{explain}\:{it}\:{further} \\ $$
Commented by mr W last updated on 10/Mar/21

Commented by mr W last updated on 10/Mar/21

$${AD}={BD}={CD}=\mathrm{1} \\ $$$${AC}={BC}={CA}=\mathrm{1} \\ $$$${OA}=\frac{\mathrm{2}}{\mathrm{3}}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$$\mathrm{cos}\:\theta=\frac{{OA}}{{AD}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$$\mid{a}+{b}+{c}\mid=\mid{a}\mid\:\mathrm{sin}\:\theta+\mid{b}\mid\:\mathrm{sin}\:\theta+\mid{c}\mid\:\mathrm{sin}\:\theta \\ $$$$=\mathrm{3}\mid{a}\mid\:\mathrm{sin}\:\theta \\ $$$$=\mathrm{3}\mid{a}\mid\sqrt{\mathrm{1}−\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} }=\sqrt{\mathrm{6}}\mid{a}\mid=\sqrt{\mathrm{6}} \\ $$$$\Rightarrow\mid{a}\mid=\mathrm{1} \\ $$
