Menu Close

Question-135099

Tinku Tara 0 Comments
Pin




Question Number 135099 by 0731619177 last updated on 10/Mar/21
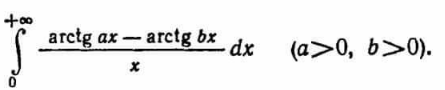
Answered by Dwaipayan Shikari last updated on 10/Mar/21
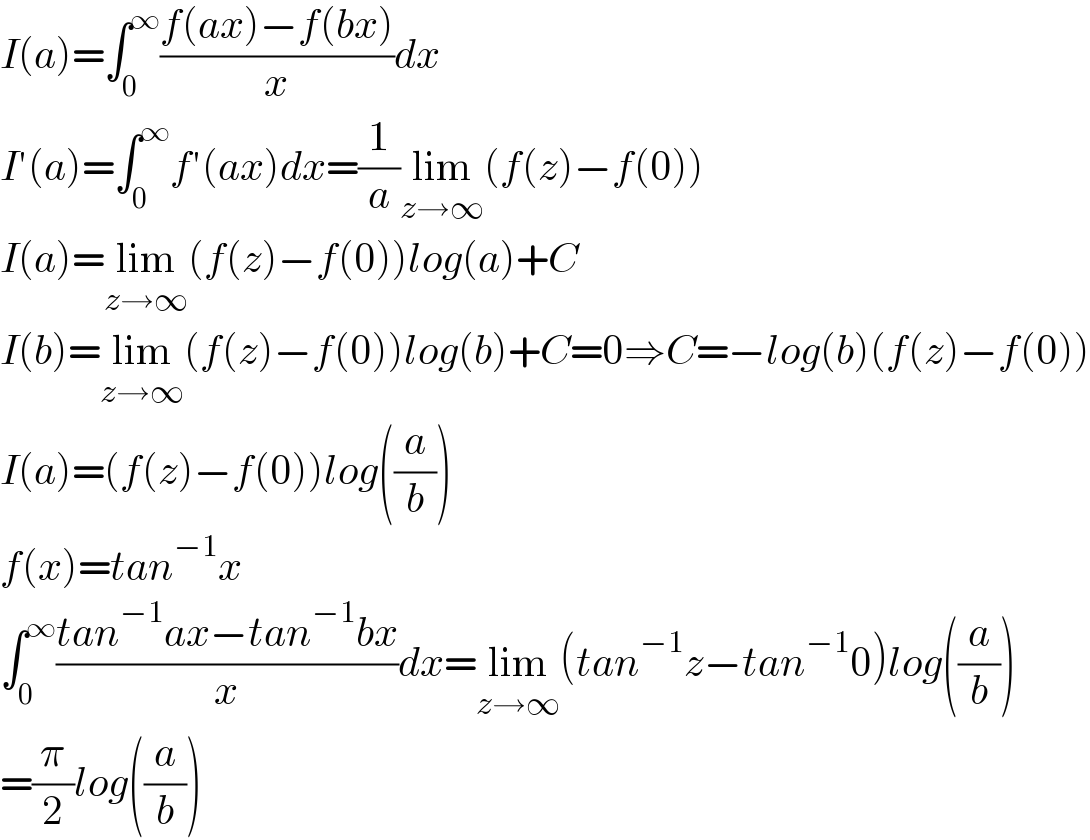
I(a)=∫_0 ^∞ ((f(ax)−f(bx))/x)dx I′(a)=∫_0 ^∞ f′(ax)dx=(1/a)lim_(z→∞) (f(z)−f(0)) I(a)=lim_(z→∞) (f(z)−f(0))log(a)+C I(b)=lim_(z→∞) (f(z)−f(0))log(b)+C=0⇒C=−log(b)(f(z)−f(0)) I(a)=(f(z)−f(0))log((a/b)) f(x)=tan^(−1) x ∫_0 ^∞ ((tan^(−1) ax−tan^(−1) bx)/x)dx=lim_(z→∞) (tan^(−1) z−tan^(−1) 0)log((a/b)) =(π/2)log((a/b))
$${I}\left({a}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{f}\left({ax}\right)−{f}\left({bx}\right)}{{x}}{dx} \\ $$$${I}'\left({a}\right)=\int_{\mathrm{0}} ^{\infty} {f}'\left({ax}\right){dx}=\frac{\mathrm{1}}{{a}}\underset{{z}\rightarrow\infty} {\mathrm{lim}}\left({f}\left({z}\right)−{f}\left(\mathrm{0}\right)\right) \\ $$$${I}\left({a}\right)=\underset{{z}\rightarrow\infty} {\mathrm{lim}}\left({f}\left({z}\right)−{f}\left(\mathrm{0}\right)\right){log}\left({a}\right)+{C} \\ $$$${I}\left({b}\right)=\underset{{z}\rightarrow\infty} {\mathrm{lim}}\left({f}\left({z}\right)−{f}\left(\mathrm{0}\right)\right){log}\left({b}\right)+{C}=\mathrm{0}\Rightarrow{C}=−{log}\left({b}\right)\left({f}\left({z}\right)−{f}\left(\mathrm{0}\right)\right) \\ $$$${I}\left({a}\right)=\left({f}\left({z}\right)−{f}\left(\mathrm{0}\right)\right){log}\left(\frac{{a}}{{b}}\right) \\ $$$${f}\left({x}\right)={tan}^{−\mathrm{1}} {x} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{tan}^{−\mathrm{1}} {ax}−{tan}^{−\mathrm{1}} {bx}}{{x}}{dx}=\underset{{z}\rightarrow\infty} {\mathrm{lim}}\left({tan}^{−\mathrm{1}} {z}−{tan}^{−\mathrm{1}} \mathrm{0}\right){log}\left(\frac{{a}}{{b}}\right) \\ $$$$=\frac{\pi}{\mathrm{2}}{log}\left(\frac{{a}}{{b}}\right) \\ $$
Answered by Ñï= last updated on 10/Mar/21
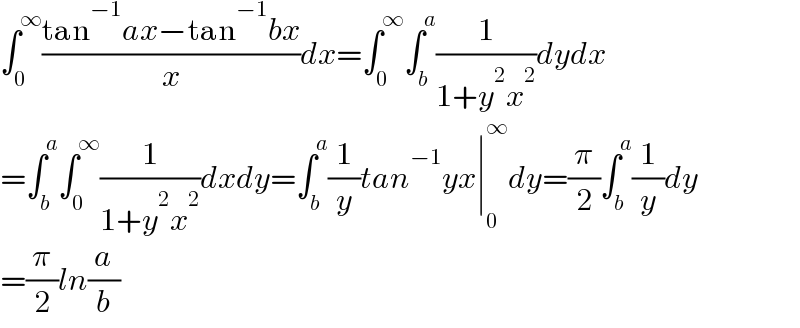
∫_0 ^∞ ((tan^(−1) ax−tan^(−1) bx)/x)dx=∫_0 ^∞ ∫_b ^a (1/(1+y^2 x^2 ))dydx =∫_b ^a ∫_0 ^∞ (1/(1+y^2 x^2 ))dxdy=∫_b ^a (1/y)tan^(−1) yx∣_0 ^∞ dy=(π/2)∫_b ^a (1/y)dy =(π/2)ln(a/b)
$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{tan}^{−\mathrm{1}} {ax}−\mathrm{tan}^{−\mathrm{1}} {bx}}{{x}}{dx}=\int_{\mathrm{0}} ^{\infty} \int_{{b}} ^{{a}} \frac{\mathrm{1}}{\mathrm{1}+{y}^{\mathrm{2}} {x}^{\mathrm{2}} }{dydx} \\ $$$$=\int_{{b}} ^{{a}} \int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{1}+{y}^{\mathrm{2}} {x}^{\mathrm{2}} }{dxdy}=\int_{{b}} ^{{a}} \frac{\mathrm{1}}{{y}}{tan}^{−\mathrm{1}} {yx}\mid_{\mathrm{0}} ^{\infty} {dy}=\frac{\pi}{\mathrm{2}}\int_{{b}} ^{{a}} \frac{\mathrm{1}}{{y}}{dy} \\ $$$$=\frac{\pi}{\mathrm{2}}{ln}\frac{{a}}{{b}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *