Question Number 135128 by bramlexs22 last updated on 10/Mar/21
Commented by mr W last updated on 10/Mar/21
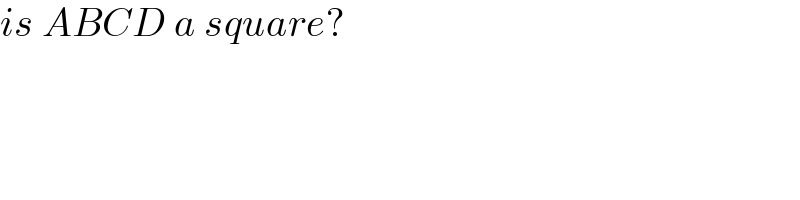
$${is}\:{ABCD}\:{a}\:{square}? \\ $$
Commented by mr W last updated on 10/Mar/21
Commented by bramlexs22 last updated on 10/Mar/21

$$\mathrm{yes}\: \\ $$
Commented by bramlexs22 last updated on 10/Mar/21

$$\mathrm{is}\:\measuredangle\mathrm{AEB}\:=\:\mathrm{135}° \\ $$
Answered by mr W last updated on 10/Mar/21
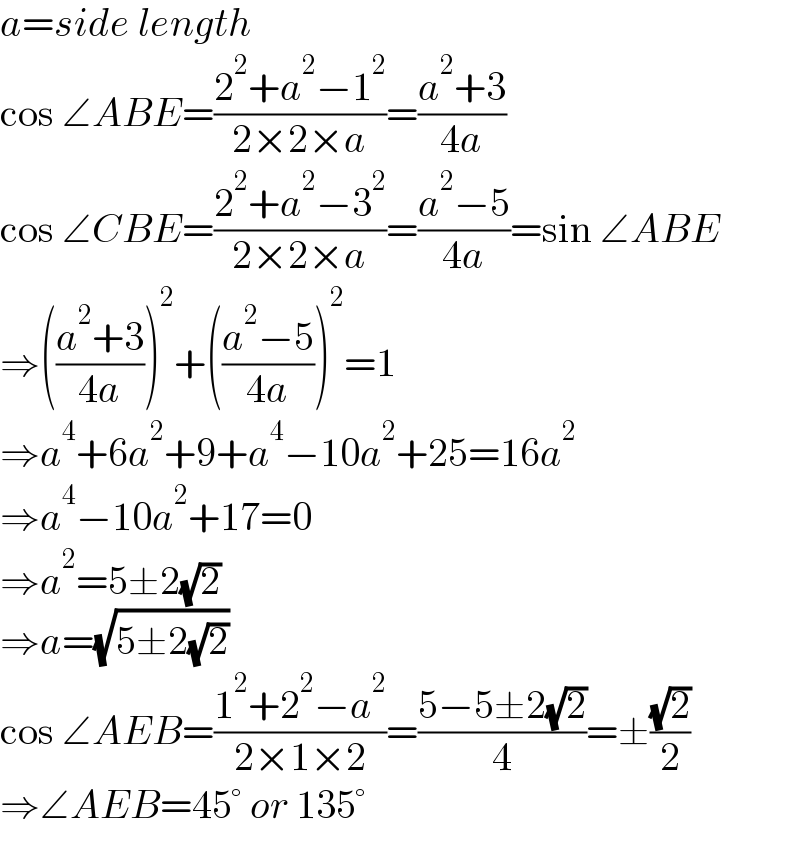
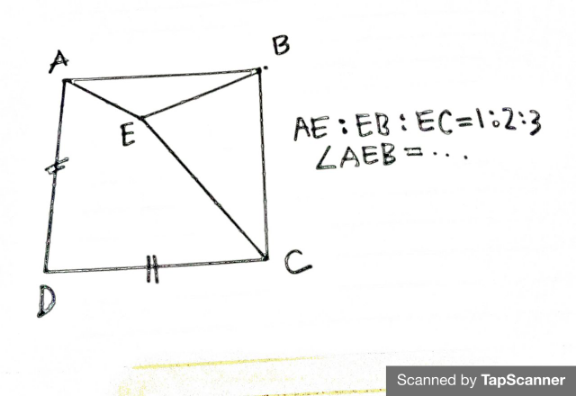
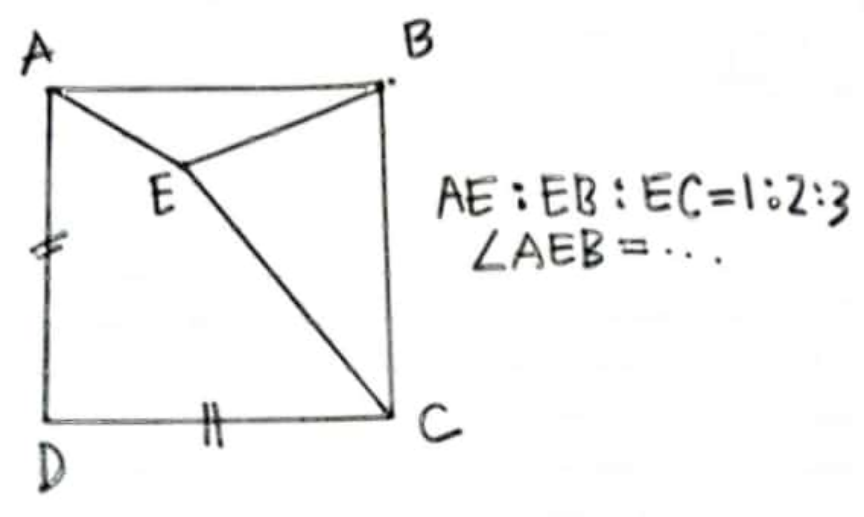
$${a}={side}\:{length} \\ $$$$\mathrm{cos}\:\angle{ABE}=\frac{\mathrm{2}^{\mathrm{2}} +{a}^{\mathrm{2}} −\mathrm{1}^{\mathrm{2}} }{\mathrm{2}×\mathrm{2}×{a}}=\frac{{a}^{\mathrm{2}} +\mathrm{3}}{\mathrm{4}{a}} \\ $$$$\mathrm{cos}\:\angle{CBE}=\frac{\mathrm{2}^{\mathrm{2}} +{a}^{\mathrm{2}} −\mathrm{3}^{\mathrm{2}} }{\mathrm{2}×\mathrm{2}×{a}}=\frac{{a}^{\mathrm{2}} −\mathrm{5}}{\mathrm{4}{a}}=\mathrm{sin}\:\angle{ABE} \\ $$$$\Rightarrow\left(\frac{{a}^{\mathrm{2}} +\mathrm{3}}{\mathrm{4}{a}}\right)^{\mathrm{2}} +\left(\frac{{a}^{\mathrm{2}} −\mathrm{5}}{\mathrm{4}{a}}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow{a}^{\mathrm{4}} +\mathrm{6}{a}^{\mathrm{2}} +\mathrm{9}+{a}^{\mathrm{4}} −\mathrm{10}{a}^{\mathrm{2}} +\mathrm{25}=\mathrm{16}{a}^{\mathrm{2}} \\ $$$$\Rightarrow{a}^{\mathrm{4}} −\mathrm{10}{a}^{\mathrm{2}} +\mathrm{17}=\mathrm{0} \\ $$$$\Rightarrow{a}^{\mathrm{2}} =\mathrm{5}\pm\mathrm{2}\sqrt{\mathrm{2}} \\ $$$$\Rightarrow{a}=\sqrt{\mathrm{5}\pm\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$\mathrm{cos}\:\angle{AEB}=\frac{\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}×\mathrm{1}×\mathrm{2}}=\frac{\mathrm{5}−\mathrm{5}\pm\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{4}}=\pm\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$\Rightarrow\angle{AEB}=\mathrm{45}°\:{or}\:\mathrm{135}° \\ $$
Commented by EDWIN88 last updated on 10/Mar/21

I prefer the angle is obtuse sir
Commented by bramlexs22 last updated on 10/Mar/21

$$\mathrm{yes}… \\ $$
Commented by mr W last updated on 10/Mar/21
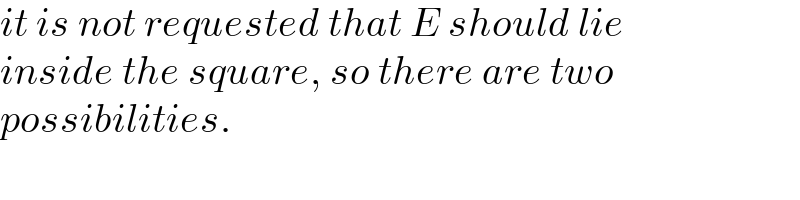
$${it}\:{is}\:{not}\:{requested}\:{that}\:{E}\:{should}\:{lie} \\ $$$${inside}\:{the}\:{square},\:{so}\:{there}\:{are}\:{two} \\ $$$${possibilities}. \\ $$
Commented by mr W last updated on 10/Mar/21
Commented by mr W last updated on 10/Mar/21
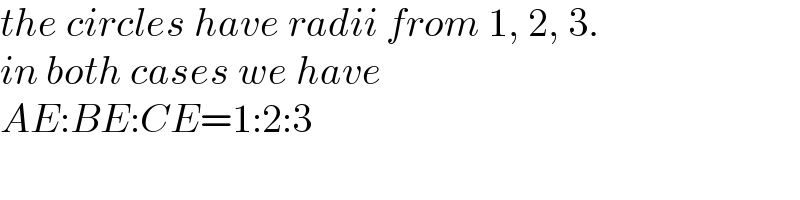
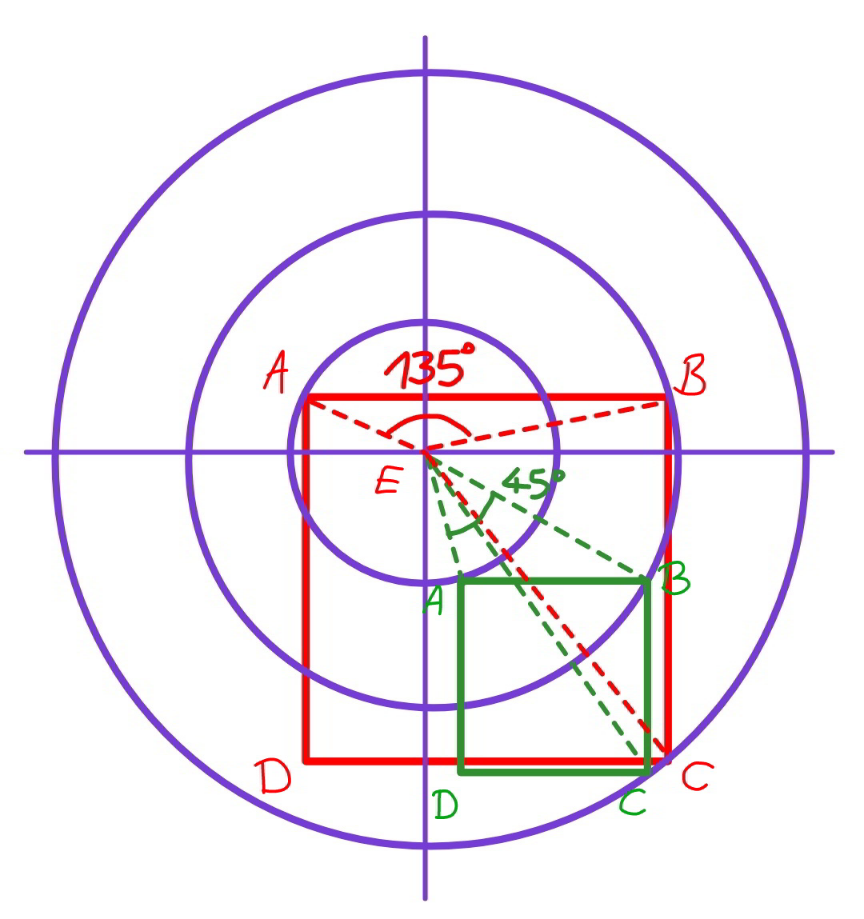
$${the}\:{circles}\:{have}\:{radii}\:{from}\:\mathrm{1},\:\mathrm{2},\:\mathrm{3}. \\ $$$${in}\:{both}\:{cases}\:{we}\:{have} \\ $$$${AE}:{BE}:{CE}=\mathrm{1}:\mathrm{2}:\mathrm{3} \\ $$
