Question Number 135206 by victoras last updated on 11/Mar/21

Answered by Olaf last updated on 11/Mar/21
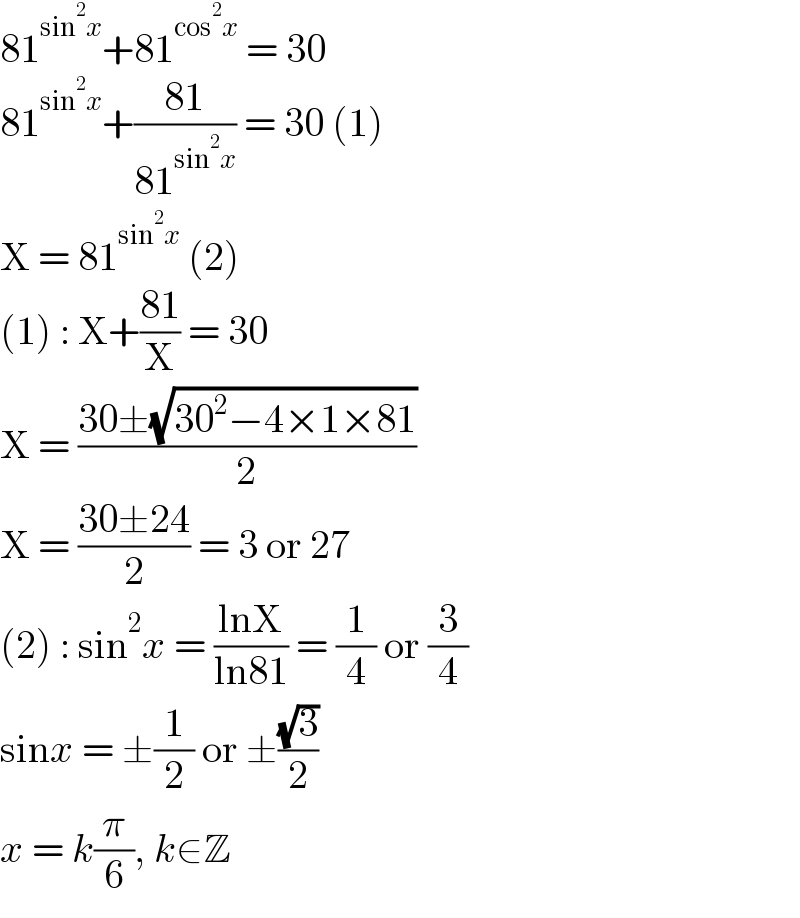
$$\mathrm{81}^{\mathrm{sin}^{\mathrm{2}} {x}} +\mathrm{81}^{\mathrm{cos}^{\mathrm{2}} {x}} \:=\:\mathrm{30} \\ $$$$\mathrm{81}^{\mathrm{sin}^{\mathrm{2}} {x}} +\frac{\mathrm{81}}{\mathrm{81}^{\mathrm{sin}^{\mathrm{2}} {x}} }\:=\:\mathrm{30}\:\left(\mathrm{1}\right) \\ $$$$\mathrm{X}\:=\:\mathrm{81}^{\mathrm{sin}^{\mathrm{2}} {x}} \:\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right)\::\:\mathrm{X}+\frac{\mathrm{81}}{\mathrm{X}}\:=\:\mathrm{30} \\ $$$$\mathrm{X}\:=\:\frac{\mathrm{30}\pm\sqrt{\mathrm{30}^{\mathrm{2}} −\mathrm{4}×\mathrm{1}×\mathrm{81}}}{\mathrm{2}} \\ $$$$\mathrm{X}\:=\:\frac{\mathrm{30}\pm\mathrm{24}}{\mathrm{2}}\:=\:\mathrm{3}\:\mathrm{or}\:\mathrm{27} \\ $$$$\left(\mathrm{2}\right)\::\:\mathrm{sin}^{\mathrm{2}} {x}\:=\:\frac{\mathrm{lnX}}{\mathrm{ln81}}\:=\:\frac{\mathrm{1}}{\mathrm{4}}\:\mathrm{or}\:\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\mathrm{sin}{x}\:=\:\pm\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{or}\:\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${x}\:=\:{k}\frac{\pi}{\mathrm{6}},\:{k}\in\mathbb{Z} \\ $$
