Question Number 135217 by benjo_mathlover last updated on 11/Mar/21
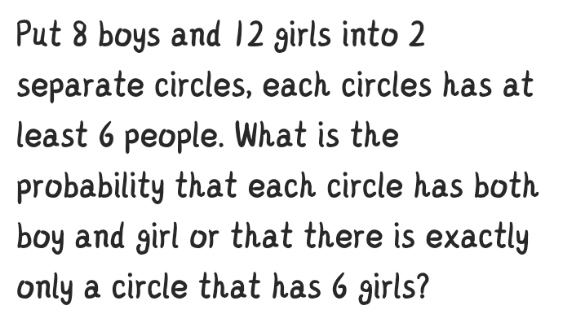
Commented by mr W last updated on 11/Mar/21
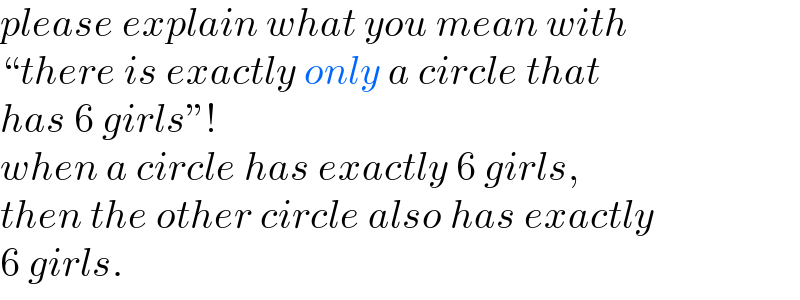
$${please}\:{explain}\:{what}\:{you}\:{mean}\:{with} \\ $$$$“{there}\:{is}\:{exactly}\:{only}\:{a}\:{circle}\:{that} \\ $$$${has}\:\mathrm{6}\:{girls}''! \\ $$$${when}\:{a}\:{circle}\:{has}\:{exactly}\:\mathrm{6}\:{girls}, \\ $$$${then}\:{the}\:{other}\:{circle}\:{also}\:{has}\:{exactly} \\ $$$$\mathrm{6}\:{girls}. \\ $$
Commented by benjo_mathlover last updated on 11/Mar/21

$$ \\ $$one of the circles exactly 6 girls means there shouldn't be a boy among them
Commented by mr W last updated on 11/Mar/21
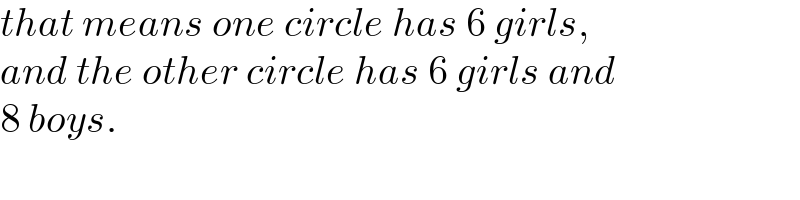
$${that}\:{means}\:{one}\:{circle}\:{has}\:\mathrm{6}\:{girls}, \\ $$$${and}\:{the}\:{other}\:{circle}\:{has}\:\mathrm{6}\:{girls}\:{and} \\ $$$$\mathrm{8}\:{boys}. \\ $$
Commented by benjo_mathlover last updated on 11/Mar/21

$${yes}\:{sir} \\ $$
Commented by mr W last updated on 11/Mar/21
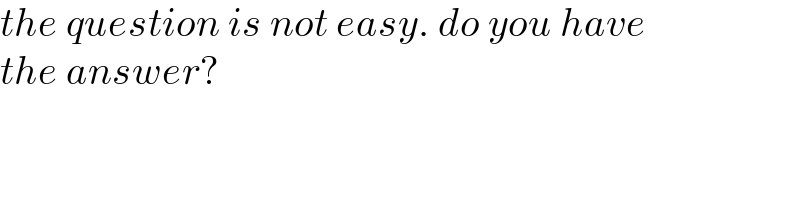
$${the}\:{question}\:{is}\:{not}\:{easy}.\:{do}\:{you}\:{have} \\ $$$${the}\:{answer}? \\ $$
Answered by mr W last updated on 12/Mar/21
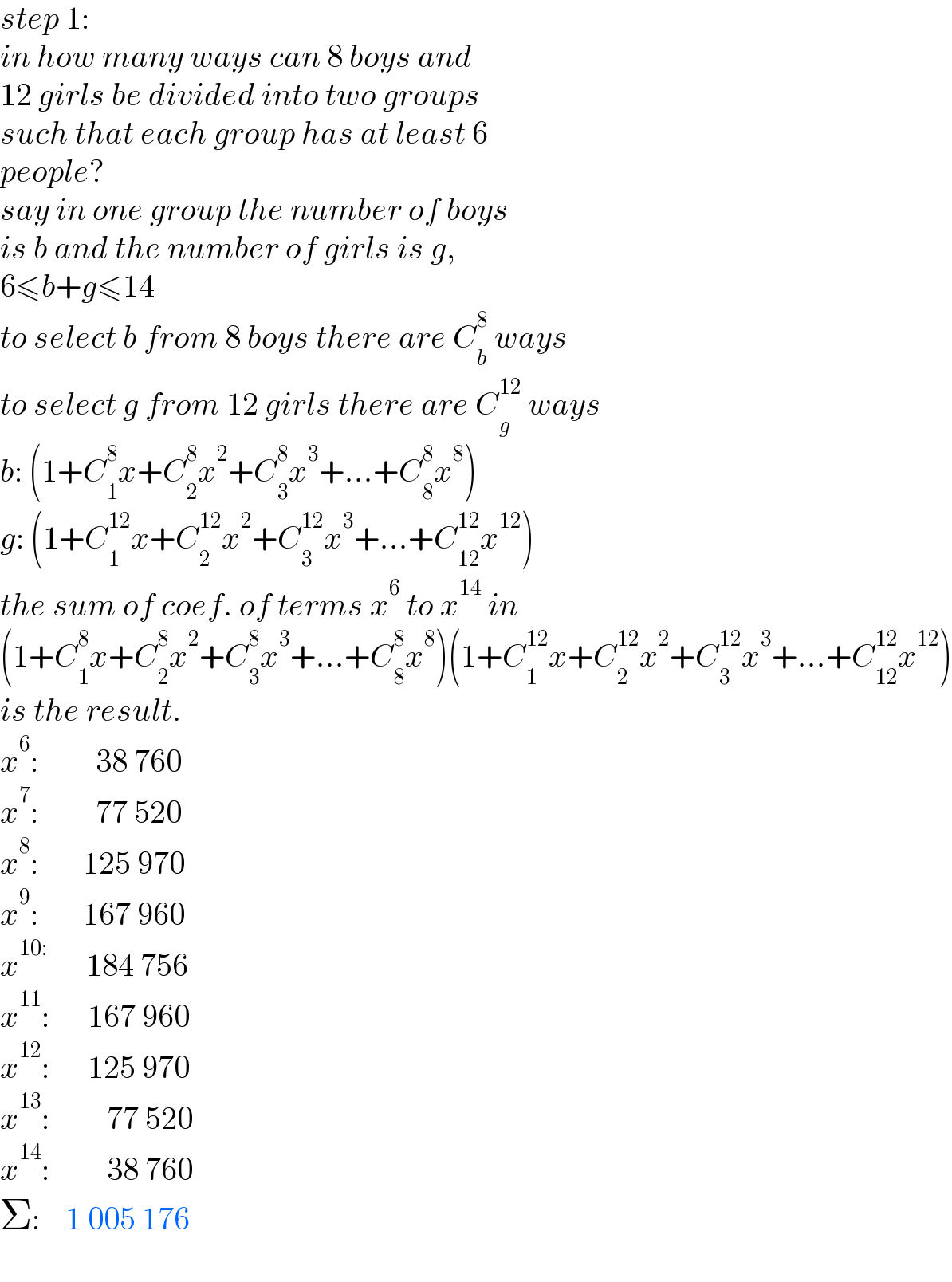
$${step}\:\mathrm{1}: \\ $$$${in}\:{how}\:{many}\:{ways}\:{can}\:\mathrm{8}\:{boys}\:{and} \\ $$$$\mathrm{12}\:{girls}\:{be}\:{divided}\:{into}\:{two}\:{groups} \\ $$$${such}\:{that}\:{each}\:{group}\:{has}\:{at}\:{least}\:\mathrm{6} \\ $$$${people}? \\ $$$${say}\:{in}\:{one}\:{group}\:{the}\:{number}\:{of}\:{boys} \\ $$$${is}\:{b}\:{and}\:{the}\:{number}\:{of}\:{girls}\:{is}\:{g}, \\ $$$$\mathrm{6}\leqslant{b}+{g}\leqslant\mathrm{14} \\ $$$${to}\:{select}\:{b}\:{from}\:\mathrm{8}\:{boys}\:{there}\:{are}\:{C}_{{b}} ^{\mathrm{8}} \:{ways} \\ $$$${to}\:{select}\:{g}\:{from}\:\mathrm{12}\:{girls}\:{there}\:{are}\:{C}_{{g}} ^{\mathrm{12}} \:{ways} \\ $$$${b}:\:\left(\mathrm{1}+{C}_{\mathrm{1}} ^{\mathrm{8}} {x}+{C}_{\mathrm{2}} ^{\mathrm{8}} {x}^{\mathrm{2}} +{C}_{\mathrm{3}} ^{\mathrm{8}} {x}^{\mathrm{3}} +…+{C}_{\mathrm{8}} ^{\mathrm{8}} {x}^{\mathrm{8}} \right) \\ $$$${g}:\:\left(\mathrm{1}+{C}_{\mathrm{1}} ^{\mathrm{12}} {x}+{C}_{\mathrm{2}} ^{\mathrm{12}} {x}^{\mathrm{2}} +{C}_{\mathrm{3}} ^{\mathrm{12}} {x}^{\mathrm{3}} +…+{C}_{\mathrm{12}} ^{\mathrm{12}} {x}^{\mathrm{12}} \right) \\ $$$${the}\:{sum}\:{of}\:{coef}.\:{of}\:{terms}\:{x}^{\mathrm{6}} \:{to}\:{x}^{\mathrm{14}} \:{in} \\ $$$$\left(\mathrm{1}+{C}_{\mathrm{1}} ^{\mathrm{8}} {x}+{C}_{\mathrm{2}} ^{\mathrm{8}} {x}^{\mathrm{2}} +{C}_{\mathrm{3}} ^{\mathrm{8}} {x}^{\mathrm{3}} +…+{C}_{\mathrm{8}} ^{\mathrm{8}} {x}^{\mathrm{8}} \right)\left(\mathrm{1}+{C}_{\mathrm{1}} ^{\mathrm{12}} {x}+{C}_{\mathrm{2}} ^{\mathrm{12}} {x}^{\mathrm{2}} +{C}_{\mathrm{3}} ^{\mathrm{12}} {x}^{\mathrm{3}} +…+{C}_{\mathrm{12}} ^{\mathrm{12}} {x}^{\mathrm{12}} \right) \\ $$$${is}\:{the}\:{result}. \\ $$$${x}^{\mathrm{6}} :\:\:\:\:\:\:\:\:\:\mathrm{38}\:\mathrm{760} \\ $$$${x}^{\mathrm{7}} :\:\:\:\:\:\:\:\:\:\mathrm{77}\:\mathrm{520} \\ $$$${x}^{\mathrm{8}} :\:\:\:\:\:\:\:\mathrm{125}\:\mathrm{970} \\ $$$${x}^{\mathrm{9}} :\:\:\:\:\:\:\:\mathrm{167}\:\mathrm{960} \\ $$$${x}^{\mathrm{10}:} \:\:\:\:\:\:\mathrm{184}\:\mathrm{756} \\ $$$${x}^{\mathrm{11}} :\:\:\:\:\:\:\mathrm{167}\:\mathrm{960} \\ $$$${x}^{\mathrm{12}} :\:\:\:\:\:\:\mathrm{125}\:\mathrm{970} \\ $$$${x}^{\mathrm{13}} :\:\:\:\:\:\:\:\:\:\mathrm{77}\:\mathrm{520} \\ $$$${x}^{\mathrm{14}} :\:\:\:\:\:\:\:\:\:\mathrm{38}\:\mathrm{760} \\ $$$$\Sigma:\:\:\:\:\mathrm{1}\:\mathrm{005}\:\mathrm{176} \\ $$
Commented by mr W last updated on 12/Mar/21

$${step}\:\mathrm{2}: \\ $$$${as}\:{step}\:\mathrm{1},\:{but}\:{each}\:{group}\:{must}\:{have} \\ $$$${both}\:{boy}\:{and}\:{girl},\:{that}\:{means}\:{one} \\ $$$${group}\:{must}\:{have}\:{at}\:{least}\:{one}\:{but} \\ $$$${at}\:{most}\:\mathrm{7}\:{boys},\:{and}\:{at}\:{least}\:{one}\:{but} \\ $$$${at}\:{most}\:\mathrm{11}\:{girls}. \\ $$$${the}\:{sum}\:{of}\:{coef}.\:{of}\:{terms}\:{x}^{\mathrm{6}} \:{to}\:{x}^{\mathrm{14}} \:{in} \\ $$$$\left({C}_{\mathrm{1}} ^{\mathrm{8}} {x}+{C}_{\mathrm{2}} ^{\mathrm{8}} {x}^{\mathrm{2}} +{C}_{\mathrm{3}} ^{\mathrm{8}} {x}^{\mathrm{3}} +…+{C}_{\mathrm{7}} ^{\mathrm{8}} {x}^{\mathrm{7}} \right)×\left({C}_{\mathrm{1}} ^{\mathrm{12}} {x}+{C}_{\mathrm{2}} ^{\mathrm{12}} {x}^{\mathrm{2}} +{C}_{\mathrm{3}} ^{\mathrm{12}} {x}^{\mathrm{3}} +…+{C}_{\mathrm{11}} ^{\mathrm{12}} {x}^{\mathrm{11}} \right) \\ $$$${is}\:{the}\:{result}. \\ $$$${x}^{\mathrm{6}} :\:\:\:\:\:\:\:\:\:\mathrm{37}\:\mathrm{808} \\ $$$${x}^{\mathrm{7}} :\:\:\:\:\:\:\:\:\:\mathrm{76}\:\mathrm{720} \\ $$$${x}^{\mathrm{8}} :\:\:\:\:\:\:\mathrm{125}\:\mathrm{474} \\ $$$${x}^{\mathrm{9}} :\:\:\:\:\:\:\mathrm{167}\:\mathrm{728} \\ $$$${x}^{\mathrm{10}} :\:\:\:\:\:\mathrm{184}\:\mathrm{624} \\ $$$${x}^{\mathrm{11}} :\:\:\:\:\:\mathrm{167}\:\mathrm{728} \\ $$$${x}^{\mathrm{12}} :\:\:\:\:\:\mathrm{125}\:\mathrm{474} \\ $$$${x}^{\mathrm{13}} :\:\:\:\:\:\:\:\:\mathrm{76}\:\mathrm{720} \\ $$$${x}^{\mathrm{14}} :\:\:\:\:\:\:\:\:\mathrm{37}\:\mathrm{808} \\ $$$$\Sigma:\:\:\:\:\mathrm{1}\:\mathrm{000}\:\mathrm{084} \\ $$
Commented by mr W last updated on 11/Mar/21
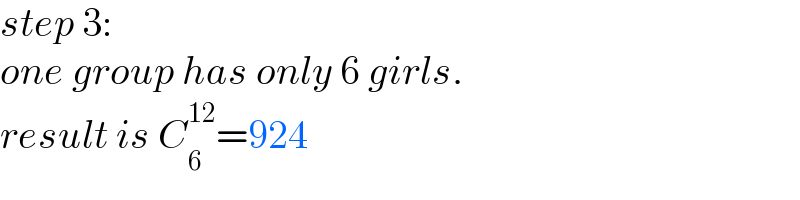
$${step}\:\mathrm{3}: \\ $$$${one}\:{group}\:{has}\:{only}\:\mathrm{6}\:{girls}. \\ $$$${result}\:{is}\:{C}_{\mathrm{6}} ^{\mathrm{12}} =\mathrm{924} \\ $$
Commented by mr W last updated on 11/Mar/21
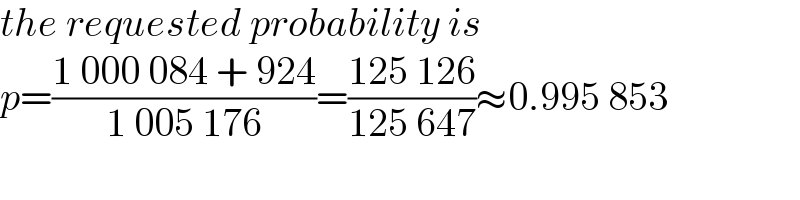
$${the}\:{requested}\:{probability}\:{is} \\ $$$${p}=\frac{\mathrm{1}\:\mathrm{000}\:\mathrm{084}\:+\:\mathrm{924}}{\mathrm{1}\:\mathrm{005}\:\mathrm{176}}=\frac{\mathrm{125}\:\mathrm{126}}{\mathrm{125}\:\mathrm{647}}\approx\mathrm{0}.\mathrm{995}\:\mathrm{853} \\ $$
Commented by mr W last updated on 11/Mar/21

Commented by mr W last updated on 11/Mar/21

Commented by benjo_mathlover last updated on 13/Mar/21

$${waw}=.==== \\ $$
Commented by mr W last updated on 13/Mar/21
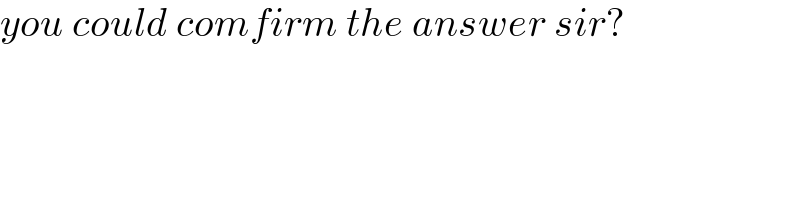
$${you}\:{could}\:{comfirm}\:{the}\:{answer}\:{sir}? \\ $$
