Question Number 135308 by bobhans last updated on 12/Mar/21

Commented by mr W last updated on 12/Mar/21

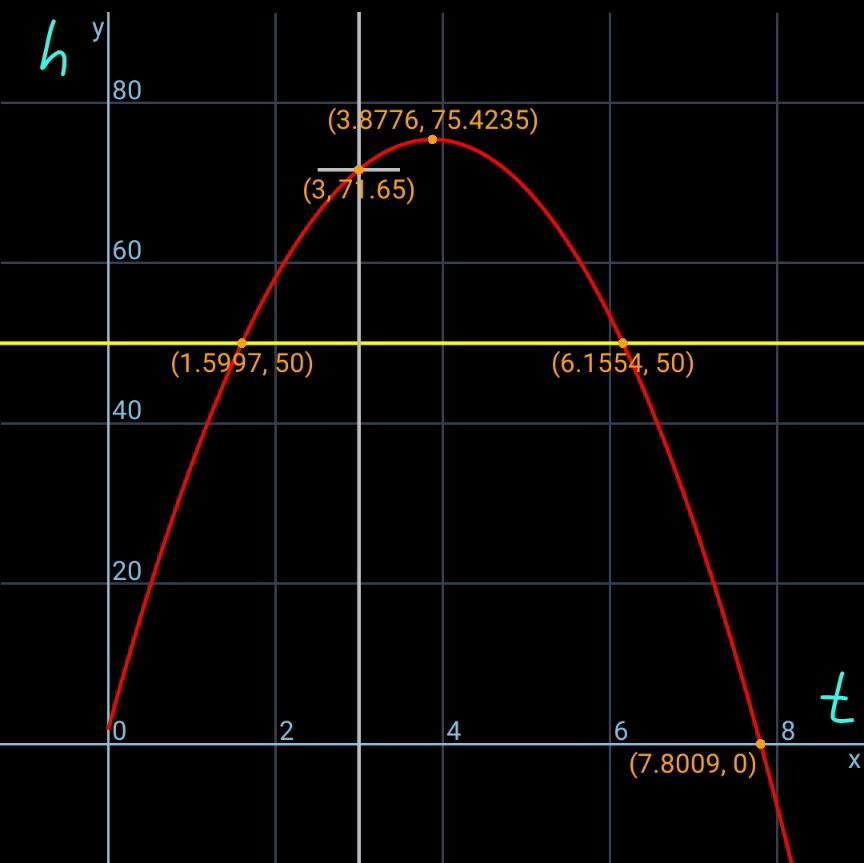
$${at}\:{t}=\mathrm{3}\:{s},\:{the}\:{height}\:{is}\:\mathrm{71}.\mathrm{65}{m} \\ $$$${at}\:{t}=\mathrm{7}.\mathrm{8009}{s},\:{the}\:{ball}\:{hits}\:{the}\:{ground} \\ $$$${max}.\:{height}\:{is}\:\mathrm{75}.\mathrm{4235}{m} \\ $$$${in}\:\mathrm{6}.\mathrm{1554}−\mathrm{1}.\mathrm{5997}=\mathrm{4}.\mathrm{5557}{s}\:{the}\:{ball} \\ $$$${is}\:{above}\:\mathrm{50}{m} \\ $$
Commented by mr W last updated on 12/Mar/21
Answered by Dwaipayan Shikari last updated on 12/Mar/21
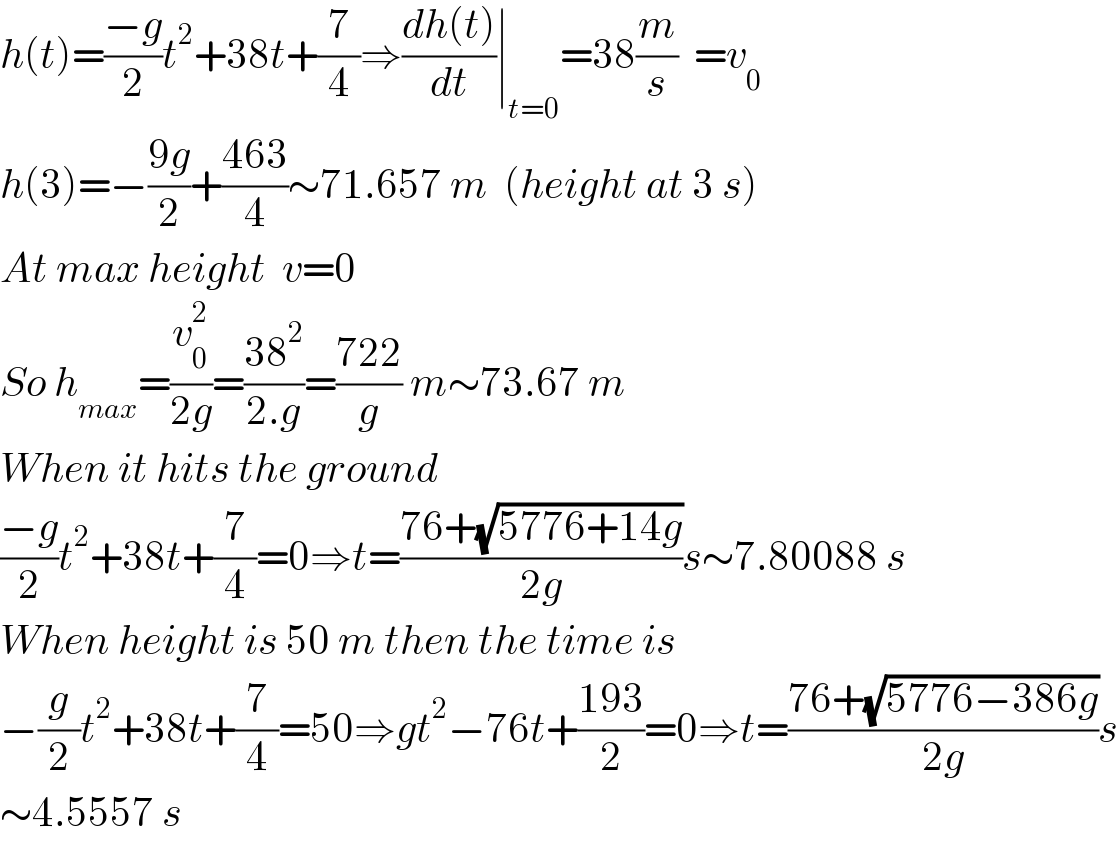
$${h}\left({t}\right)=\frac{−{g}}{\mathrm{2}}{t}^{\mathrm{2}} +\mathrm{38}{t}+\frac{\mathrm{7}}{\mathrm{4}}\Rightarrow\frac{{dh}\left({t}\right)}{{dt}}\mid_{{t}=\mathrm{0}} =\mathrm{38}\frac{{m}}{{s}}\:\:={v}_{\mathrm{0}} \\ $$$${h}\left(\mathrm{3}\right)=−\frac{\mathrm{9}{g}}{\mathrm{2}}+\frac{\mathrm{463}}{\mathrm{4}}\sim\mathrm{71}.\mathrm{657}\:{m}\:\:\left({height}\:{at}\:\mathrm{3}\:{s}\right) \\ $$$${At}\:{max}\:{height}\:\:{v}=\mathrm{0} \\ $$$${So}\:{h}_{{max}} =\frac{{v}_{\mathrm{0}} ^{\mathrm{2}} }{\mathrm{2}{g}}=\frac{\mathrm{38}^{\mathrm{2}} }{\mathrm{2}.{g}}=\frac{\mathrm{722}}{{g}}\:{m}\sim\mathrm{73}.\mathrm{67}\:{m} \\ $$$${When}\:{it}\:{hits}\:{the}\:{ground}\: \\ $$$$\frac{−{g}}{\mathrm{2}}{t}^{\mathrm{2}} +\mathrm{38}{t}+\frac{\mathrm{7}}{\mathrm{4}}=\mathrm{0}\Rightarrow{t}=\frac{\mathrm{76}+\sqrt{\mathrm{5776}+\mathrm{14}{g}}}{\mathrm{2}{g}}{s}\sim\mathrm{7}.\mathrm{80088}\:{s} \\ $$$${When}\:{height}\:{is}\:\mathrm{50}\:{m}\:{then}\:{the}\:{time}\:{is}\: \\ $$$$−\frac{{g}}{\mathrm{2}}{t}^{\mathrm{2}} +\mathrm{38}{t}+\frac{\mathrm{7}}{\mathrm{4}}=\mathrm{50}\Rightarrow{gt}^{\mathrm{2}} −\mathrm{76}{t}+\frac{\mathrm{193}}{\mathrm{2}}=\mathrm{0}\Rightarrow{t}=\frac{\mathrm{76}+\sqrt{\mathrm{5776}−\mathrm{386}{g}}}{\mathrm{2}{g}}{s} \\ $$$$\sim\mathrm{4}.\mathrm{5557}\:{s} \\ $$
