Menu Close

Question-135421

Tinku Tara 0 Comments
Pin




Question Number 135421 by benjo_mathlover last updated on 13/Mar/21
Commented by mr W last updated on 13/Mar/21
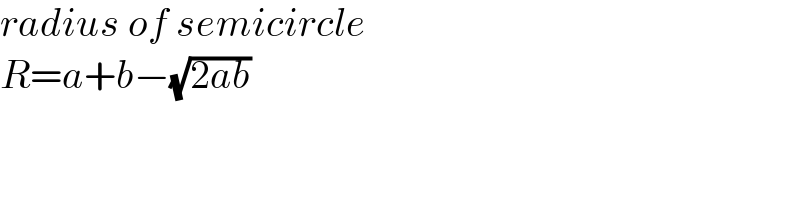
radius of semicircle R=a+b−(√(2ab))
$${radius}\:{of}\:{semicircle} \\ $$$${R}={a}+{b}−\sqrt{\mathrm{2}{ab}} \\ $$
Commented by EDWIN88 last updated on 13/Mar/21
Commented by EDWIN88 last updated on 13/Mar/21
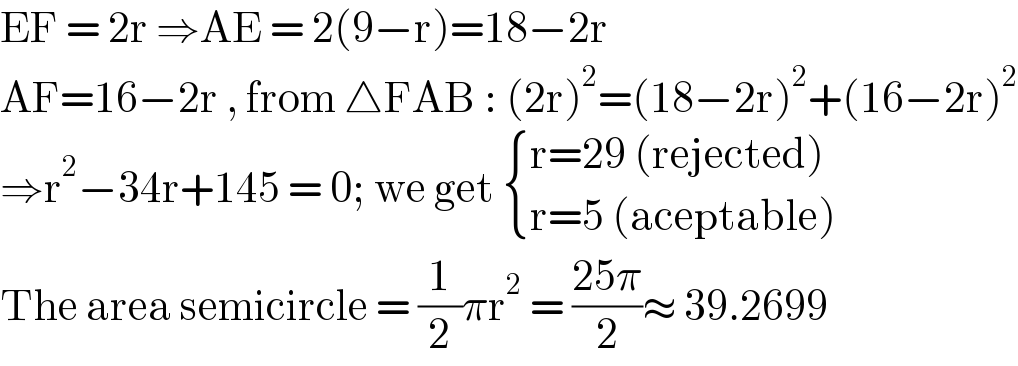
EF = 2r ⇒AE = 2(9−r)=18−2r AF=16−2r , from △FAB : (2r)^2 =(18−2r)^2 +(16−2r)^2 ⇒r^2 −34r+145 = 0; we get { ((r=29 (rejected))),((r=5 (aceptable))) :} The area semicircle = (1/2)πr^2 = ((25π)/2)≈ 39.2699
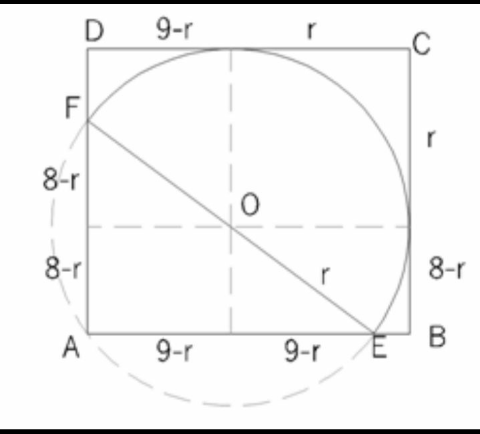
$$\mathrm{EF}\:=\:\mathrm{2r}\:\Rightarrow\mathrm{AE}\:=\:\mathrm{2}\left(\mathrm{9}−\mathrm{r}\right)=\mathrm{18}−\mathrm{2r} \\ $$$$\mathrm{AF}=\mathrm{16}−\mathrm{2r}\:,\:\mathrm{from}\:\bigtriangleup\mathrm{FAB}\::\:\left(\mathrm{2r}\right)^{\mathrm{2}} =\left(\mathrm{18}−\mathrm{2r}\right)^{\mathrm{2}} +\left(\mathrm{16}−\mathrm{2r}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{r}^{\mathrm{2}} −\mathrm{34r}+\mathrm{145}\:=\:\mathrm{0};\:\mathrm{we}\:\mathrm{get}\:\begin{cases}{\mathrm{r}=\mathrm{29}\:\left(\mathrm{rejected}\right)}\\{\mathrm{r}=\mathrm{5}\:\left(\mathrm{aceptable}\right)}\end{cases} \\ $$$$\mathrm{The}\:\mathrm{area}\:\mathrm{semicircle}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\pi\mathrm{r}^{\mathrm{2}} \:=\:\frac{\mathrm{25}\pi}{\mathrm{2}}\approx\:\mathrm{39}.\mathrm{2699} \\ $$
Commented by mr W last updated on 13/Mar/21
good approach!
$${good}\:{approach}! \\ $$
Answered by mr W last updated on 13/Mar/21
Commented by mr W last updated on 13/Mar/21
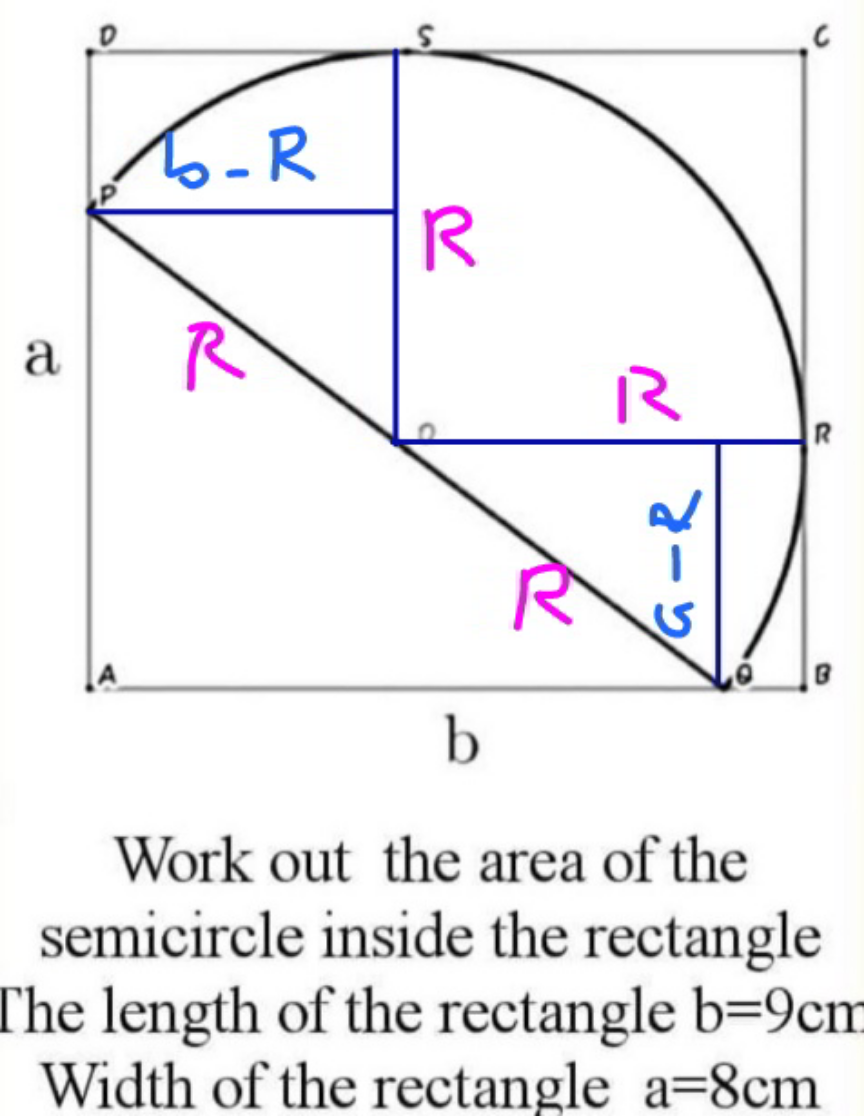
PD=R−(√(R^2 −(b−R)^2 ))=R−(√(b(2R−b))) AP=a+(√(b(2R−b)))−R QB=R−(√(R^2 −(a−R)^2 ))=R−(√(a(2R−a))) AQ=b+(√(a(2R−a)))−R [a+(√(b(2R−b)))−R]^2 +[b+(√(a(2R−a)))−R]^2 =(2R)^2 a^2 +b(2R−b)+R^2 −2aR+2(a−R)(√(b(2R−b)))+b^2 +a(2R−a)+R^2 −2bR+2(b−R)(√(a(2R−a)))=4R^2 (a−R)(√(b(2R−b)))+(b−R)(√(a(2R−a)))=R^2 (a−R)(√(b(2R−b)))=R^2 −(b−R)(√(a(2R−a))) (a^2 −2aR+R^2 )(2bR−b^2 )=R^4 +(b^2 −2bR+R^2 )(2aR−a^2 )−2R^2 (b−R)(√(a(2R−a))) 2a^2 bR−4abR^2 +2bR^3 −a^2 b^2 +2ab^2 R−b^2 R^2 =R^4 +2ab^2 R−4abR^2 +2aR^3 −a^2 b^2 +2a^2 bR−a^2 R^2 −2R^2 (b−R)(√(a(2R−a))) R^2 +2(a−b)R−(a^2 −b^2 )=2(b−R)(√(a(2R−a))) R^4 +4(a−b)^2 R^2 +(a^2 −b^2 )^2 +4(a−b)R^3 −2(a^2 −b^2 )R^2 −4(a−b)(a^2 −b^2 )R=4(b^2 −2bR+R^2 )(2aR−a^2 ) R^4 +4(a−b)^2 R^2 +(a^2 −b^2 )^2 +4(a−b)R^3 −2(a^2 −b^2 )R^2 −4(a−b)(a^2 −b^2 )R=(4b^2 −8bR+4R^2 )(2aR−a^2 ) R^4 +4(a−b)^2 R^2 +(a^2 −b^2 )^2 +4(a−b)R^3 −2(a^2 −b^2 )R^2 −4(a−b)(a^2 −b^2 )R=8ab^2 R−16abR^2 +8aR^3 −4a^2 b^2 +8a^2 bR−4a^2 R^2 R^4 −4(a+b)R^3 +2[3(a+b)^2 −2ab]R^2 −4(a+b)(a^2 +b^2 )R+(a^2 +b^2 )^2 =0 [R^2 −2(a+b)R+a^2 +b^2 ]^2 =0 ⇒R=a+b−(√(2ab)) (− rejected) with a=8, b=9 R=8+9−(√(2×8×9))=17−12=5
$${PD}={R}−\sqrt{{R}^{\mathrm{2}} −\left({b}−{R}\right)^{\mathrm{2}} }={R}−\sqrt{{b}\left(\mathrm{2}{R}−{b}\right)} \\ $$$${AP}={a}+\sqrt{{b}\left(\mathrm{2}{R}−{b}\right)}−{R} \\ $$$${QB}={R}−\sqrt{{R}^{\mathrm{2}} −\left({a}−{R}\right)^{\mathrm{2}} }={R}−\sqrt{{a}\left(\mathrm{2}{R}−{a}\right)} \\ $$$${AQ}={b}+\sqrt{{a}\left(\mathrm{2}{R}−{a}\right)}−{R} \\ $$$$\left[{a}+\sqrt{{b}\left(\mathrm{2}{R}−{b}\right)}−{R}\right]^{\mathrm{2}} +\left[{b}+\sqrt{{a}\left(\mathrm{2}{R}−{a}\right)}−{R}\right]^{\mathrm{2}} =\left(\mathrm{2}{R}\right)^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} +{b}\left(\mathrm{2}{R}−{b}\right)+{R}^{\mathrm{2}} −\mathrm{2}{aR}+\mathrm{2}\left({a}−{R}\right)\sqrt{{b}\left(\mathrm{2}{R}−{b}\right)}+{b}^{\mathrm{2}} +{a}\left(\mathrm{2}{R}−{a}\right)+{R}^{\mathrm{2}} −\mathrm{2}{bR}+\mathrm{2}\left({b}−{R}\right)\sqrt{{a}\left(\mathrm{2}{R}−{a}\right)}=\mathrm{4}{R}^{\mathrm{2}} \\ $$$$\left({a}−{R}\right)\sqrt{{b}\left(\mathrm{2}{R}−{b}\right)}+\left({b}−{R}\right)\sqrt{{a}\left(\mathrm{2}{R}−{a}\right)}={R}^{\mathrm{2}} \\ $$$$\left({a}−{R}\right)\sqrt{{b}\left(\mathrm{2}{R}−{b}\right)}={R}^{\mathrm{2}} −\left({b}−{R}\right)\sqrt{{a}\left(\mathrm{2}{R}−{a}\right)} \\ $$$$\left({a}^{\mathrm{2}} −\mathrm{2}{aR}+{R}^{\mathrm{2}} \right)\left(\mathrm{2}{bR}−{b}^{\mathrm{2}} \right)={R}^{\mathrm{4}} +\left({b}^{\mathrm{2}} −\mathrm{2}{bR}+{R}^{\mathrm{2}} \right)\left(\mathrm{2}{aR}−{a}^{\mathrm{2}} \right)−\mathrm{2}{R}^{\mathrm{2}} \left({b}−{R}\right)\sqrt{{a}\left(\mathrm{2}{R}−{a}\right)} \\ $$$$\mathrm{2}{a}^{\mathrm{2}} {bR}−\mathrm{4}{abR}^{\mathrm{2}} +\mathrm{2}{bR}^{\mathrm{3}} −{a}^{\mathrm{2}} {b}^{\mathrm{2}} +\mathrm{2}{ab}^{\mathrm{2}} {R}−{b}^{\mathrm{2}} {R}^{\mathrm{2}} ={R}^{\mathrm{4}} +\mathrm{2}{ab}^{\mathrm{2}} {R}−\mathrm{4}{abR}^{\mathrm{2}} +\mathrm{2}{aR}^{\mathrm{3}} −{a}^{\mathrm{2}} {b}^{\mathrm{2}} +\mathrm{2}{a}^{\mathrm{2}} {bR}−{a}^{\mathrm{2}} {R}^{\mathrm{2}} −\mathrm{2}{R}^{\mathrm{2}} \left({b}−{R}\right)\sqrt{{a}\left(\mathrm{2}{R}−{a}\right)} \\ $$$${R}^{\mathrm{2}} +\mathrm{2}\left({a}−{b}\right){R}−\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)=\mathrm{2}\left({b}−{R}\right)\sqrt{{a}\left(\mathrm{2}{R}−{a}\right)} \\ $$$${R}^{\mathrm{4}} +\mathrm{4}\left({a}−{b}\right)^{\mathrm{2}} {R}^{\mathrm{2}} +\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{4}\left({a}−{b}\right){R}^{\mathrm{3}} −\mathrm{2}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){R}^{\mathrm{2}} −\mathrm{4}\left({a}−{b}\right)\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){R}=\mathrm{4}\left({b}^{\mathrm{2}} −\mathrm{2}{bR}+{R}^{\mathrm{2}} \right)\left(\mathrm{2}{aR}−{a}^{\mathrm{2}} \right) \\ $$$${R}^{\mathrm{4}} +\mathrm{4}\left({a}−{b}\right)^{\mathrm{2}} {R}^{\mathrm{2}} +\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{4}\left({a}−{b}\right){R}^{\mathrm{3}} −\mathrm{2}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){R}^{\mathrm{2}} −\mathrm{4}\left({a}−{b}\right)\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){R}=\left(\mathrm{4}{b}^{\mathrm{2}} −\mathrm{8}{bR}+\mathrm{4}{R}^{\mathrm{2}} \right)\left(\mathrm{2}{aR}−{a}^{\mathrm{2}} \right) \\ $$$${R}^{\mathrm{4}} +\mathrm{4}\left({a}−{b}\right)^{\mathrm{2}} {R}^{\mathrm{2}} +\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{4}\left({a}−{b}\right){R}^{\mathrm{3}} −\mathrm{2}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){R}^{\mathrm{2}} −\mathrm{4}\left({a}−{b}\right)\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){R}=\mathrm{8}{ab}^{\mathrm{2}} {R}−\mathrm{16}{abR}^{\mathrm{2}} +\mathrm{8}{aR}^{\mathrm{3}} −\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{2}} +\mathrm{8}{a}^{\mathrm{2}} {bR}−\mathrm{4}{a}^{\mathrm{2}} {R}^{\mathrm{2}} \\ $$$${R}^{\mathrm{4}} −\mathrm{4}\left({a}+{b}\right){R}^{\mathrm{3}} +\mathrm{2}\left[\mathrm{3}\left({a}+{b}\right)^{\mathrm{2}} −\mathrm{2}{ab}\right]{R}^{\mathrm{2}} −\mathrm{4}\left({a}+{b}\right)\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right){R}+\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\left[{R}^{\mathrm{2}} −\mathrm{2}\left({a}+{b}\right){R}+{a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right]^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{R}={a}+{b}−\sqrt{\mathrm{2}{ab}}\:\:\:\:\:\:\left(−\:{rejected}\right) \\ $$$${with}\:{a}=\mathrm{8},\:{b}=\mathrm{9} \\ $$$${R}=\mathrm{8}+\mathrm{9}−\sqrt{\mathrm{2}×\mathrm{8}×\mathrm{9}}=\mathrm{17}−\mathrm{12}=\mathrm{5} \\ $$
Commented by otchereabdullai@gmail.com last updated on 13/Mar/21
The supper prof W! God is using this man in a special way to help us. More blessing from God prof.
$$\mathrm{The}\:\mathrm{supper}\:\mathrm{prof}\:\mathrm{W}!\:\mathrm{God}\:\mathrm{is}\:\mathrm{using}\:\mathrm{this} \\ $$$$\mathrm{man}\:\mathrm{in}\:\mathrm{a}\:\mathrm{special}\:\mathrm{way}\:\mathrm{to}\:\mathrm{help}\:\mathrm{us}.\:\mathrm{More}\: \\ $$$$\mathrm{blessing}\:\mathrm{from}\:\mathrm{God}\:\:\mathrm{prof}. \\ $$$$\: \\ $$
Commented by EDWIN88 last updated on 13/Mar/21
nice
$$\mathrm{nice} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *