Question Number 135513 by Gaurav500 last updated on 13/Mar/21
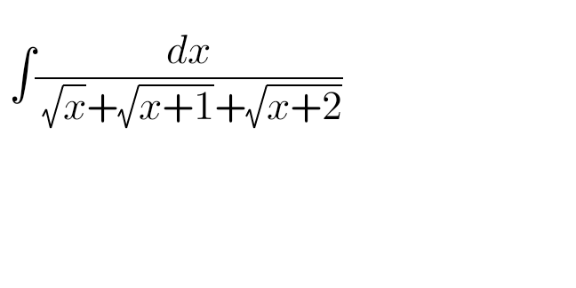
Answered by MJS_new last updated on 13/Mar/21
![∫(dx/( (√x)+(√(x+1))+(√(x+2))))= [t=x+1 → dx=dt] =∫(dt/( (√(t−1))+(√t)+(√(t+1))))=Σ_(k=1) ^6 I_k +Ci I_1 =∫(t^(3/2) /(3t^2 −4))dt I_2 =2∫((√(t−1))/(3t^2 −4))dt I_3 =∫((t(√(t−1)))/(3t^2 −4))dt I_4 =−2∫((√(t+1))/(3t^2 −4))dt I_5 =∫((t(√(t+1)))/(3t^2 −4))dt I_6 =−2∫(((√(t−1))(√t)(√(t+1)))/(3t^2 −4))dt they are all not easy. I can solve the first 5 but I found no way to solve the last one](https://www.tinkutara.com/question/Q135526.png)
$$\int\frac{{dx}}{\:\sqrt{{x}}+\sqrt{{x}+\mathrm{1}}+\sqrt{{x}+\mathrm{2}}}= \\ $$$$\:\:\:\:\:\left[{t}={x}+\mathrm{1}\:\rightarrow\:{dx}={dt}\right] \\ $$$$=\int\frac{{dt}}{\:\sqrt{{t}−\mathrm{1}}+\sqrt{{t}}+\sqrt{{t}+\mathrm{1}}}=\underset{{k}=\mathrm{1}} {\overset{\mathrm{6}} {\sum}}{I}_{{k}} \:+{Ci} \\ $$$${I}_{\mathrm{1}} =\int\frac{{t}^{\mathrm{3}/\mathrm{2}} }{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{4}}{dt} \\ $$$${I}_{\mathrm{2}} =\mathrm{2}\int\frac{\sqrt{{t}−\mathrm{1}}}{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{4}}{dt} \\ $$$${I}_{\mathrm{3}} =\int\frac{{t}\sqrt{{t}−\mathrm{1}}}{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{4}}{dt} \\ $$$${I}_{\mathrm{4}} =−\mathrm{2}\int\frac{\sqrt{{t}+\mathrm{1}}}{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{4}}{dt} \\ $$$${I}_{\mathrm{5}} =\int\frac{{t}\sqrt{{t}+\mathrm{1}}}{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{4}}{dt} \\ $$$${I}_{\mathrm{6}} =−\mathrm{2}\int\frac{\sqrt{{t}−\mathrm{1}}\sqrt{{t}}\sqrt{{t}+\mathrm{1}}}{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{4}}{dt} \\ $$$$\mathrm{they}\:\mathrm{are}\:\mathrm{all}\:\mathrm{not}\:\mathrm{easy}.\:\mathrm{I}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{first}\:\mathrm{5} \\ $$$$\mathrm{but}\:\mathrm{I}\:\mathrm{found}\:\mathrm{no}\:\mathrm{way}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{last}\:\mathrm{one} \\ $$
Commented by Gaurav500 last updated on 14/Mar/21
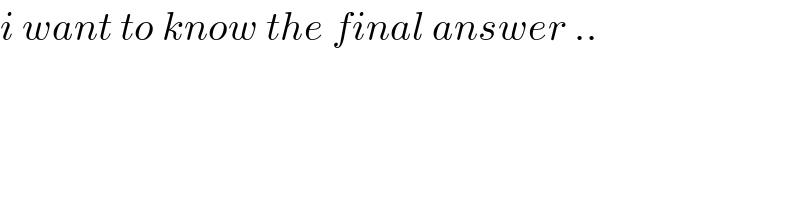
$${i}\:{want}\:{to}\:{know}\:{the}\:{final}\:{answer}\:.. \\ $$
Commented by MJS_new last updated on 14/Mar/21

$$\mathrm{me}\:\mathrm{too} \\ $$
Commented by Gaurav500 last updated on 14/Mar/21
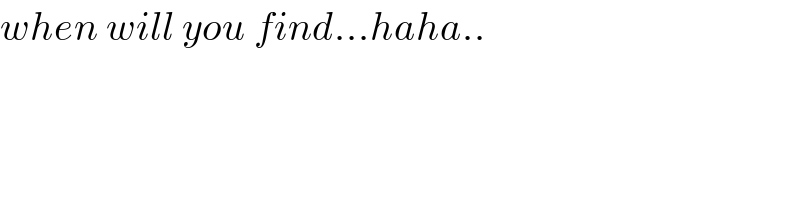
$${when}\:{will}\:{you}\:{find}…{haha}.. \\ $$
