Question-135522

Question Number 135522 by Dwaipayan Shikari last updated on 13/Mar/21

Commented by Dwaipayan Shikari last updated on 13/Mar/21

$$ \\ $$

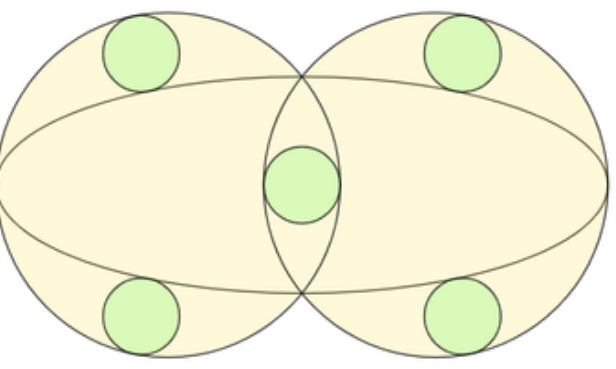
Two large circles altogether inscribe five identical small circles (in green) and an ellipse, which are each centrally and symmetrically positioned as shown above. One of the five small circles has one point of tangency with each of the large circle, whereas four others have one point of tangency with their respective large circle and one point of tangency with the ellipse.

Find the eccentricity of this ellipse

Answered by mr W last updated on 13/Mar/21

Commented by mr W last updated on 14/Mar/21

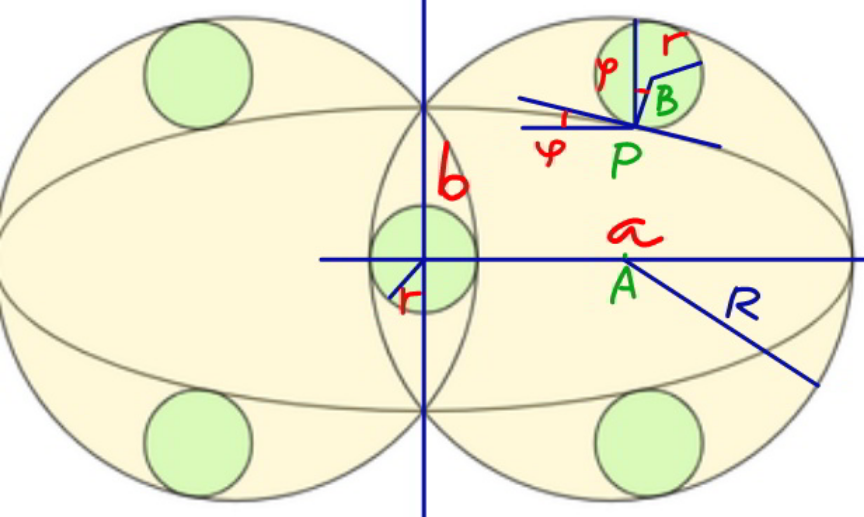
say the parameters of the ellipse are a, b. radius of small circles is r. radius of big circles is R. a=2R−r b=(√(R^2 −(R−r)^2 ))=(√((2R−r)r)) center of big circle A(R−r,0) say touch point is P(a cos θ, b sin θ) tan ϕ=−(dy/dx)=((b cos θ)/(a sin θ))=(b/(a tan θ))=(μ/(tan θ)) with μ=(b/a)=((√((2R−r)r))/(2R−r))=(√(λ/(2−λ))) with λ=(r/R) μ^2 =(λ/(2−λ)) ⇒λ=((2μ^2 )/(μ^2 +1)) ...(i) center of small circle B: x_B =a cos θ+r sin ϕ y_B =b sin θ+r cos ϕ AB=R−r (a cos θ+r sin ϕ−R+r)^2 +(b sin θ+r cos ϕ)^2 =(R−r)^2 ((a/R) cos θ+λ sin ϕ−1+λ)^2 +((b/R) sin θ+λ cos ϕ)^2 =(1−λ)^2 [(2−λ) cos θ+λ sin ϕ−1+λ]^2 +[(√((2−λ)λ)) sin θ+λ cos ϕ]^2 =(1−λ)^2 [(2−λ) cos θ+((λμ)/( (√(μ^2 +tan^2 θ))))−1+λ]^2 +[(√((2−λ)λ)) sin θ+((λ tan θ)/( (√(μ^2 +tan^2 θ))))]^2 =(1−λ)^2 ...(ii) (r/a)=(λ/(2−λ))=μ^2 i.e. when μ is maximum, r is also maximum. from (ii) we get μ_(max) ≈0.35355 at θ≈1.047 (see diagram 1) the eccentricity e=(√(1−μ^2 ))≈0.9354

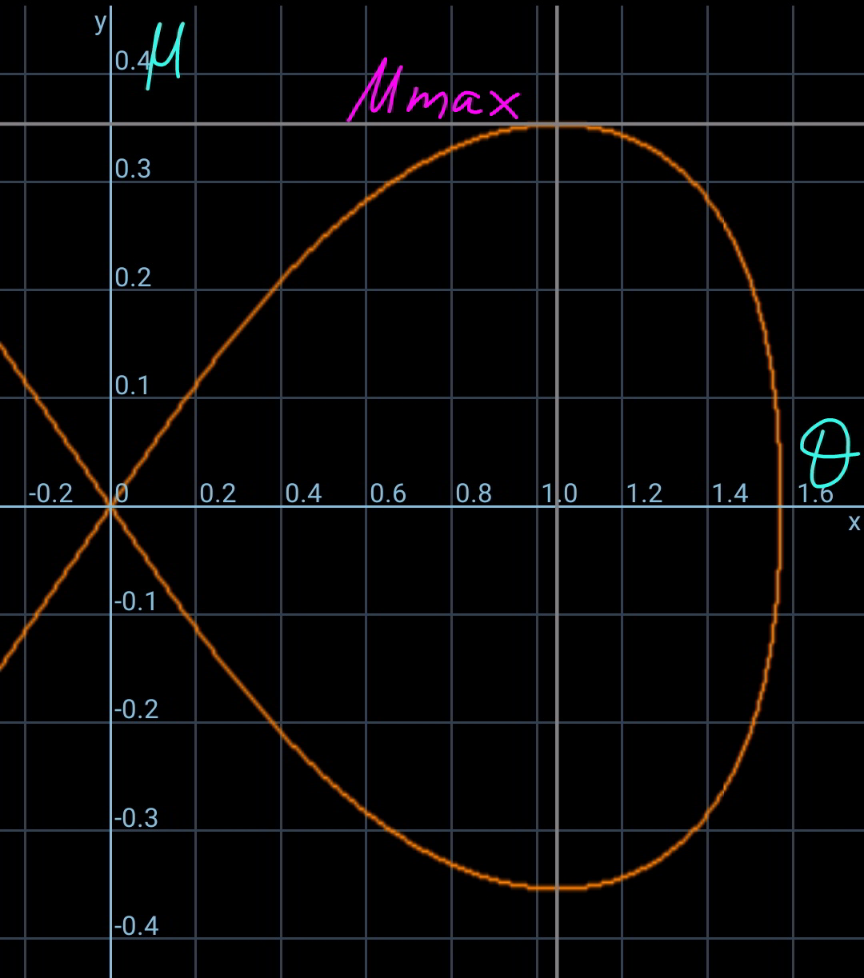
$${say}\:{the}\:{parameters}\:{of}\:{the}\:{ellipse}\:{are} \\ $$$${a},\:{b}. \\ $$$${radius}\:{of}\:{small}\:{circles}\:{is}\:{r}. \\ $$$${radius}\:{of}\:{big}\:{circles}\:{is}\:{R}. \\ $$$${a}=\mathrm{2}{R}−{r} \\ $$$${b}=\sqrt{{R}^{\mathrm{2}} −\left({R}−{r}\right)^{\mathrm{2}} }=\sqrt{\left(\mathrm{2}{R}−{r}\right){r}} \\ $$$${center}\:{of}\:{big}\:{circle}\:{A}\left({R}−{r},\mathrm{0}\right) \\ $$$$ \\ $$$${say}\:{touch}\:{point}\:{is}\:{P}\left({a}\:\mathrm{cos}\:\theta,\:{b}\:\mathrm{sin}\:\theta\right) \\ $$$$\mathrm{tan}\:\varphi=−\frac{{dy}}{{dx}}=\frac{{b}\:\mathrm{cos}\:\theta}{{a}\:\mathrm{sin}\:\theta}=\frac{{b}}{{a}\:\mathrm{tan}\:\theta}=\frac{\mu}{\mathrm{tan}\:\theta} \\ $$$${with}\:\mu=\frac{{b}}{{a}}=\frac{\sqrt{\left(\mathrm{2}{R}−{r}\right){r}}}{\mathrm{2}{R}−{r}}=\sqrt{\frac{\lambda}{\mathrm{2}−\lambda}} \\ $$$${with}\:\lambda=\frac{{r}}{{R}} \\ $$$$\mu^{\mathrm{2}} =\frac{\lambda}{\mathrm{2}−\lambda} \\ $$$$\Rightarrow\lambda=\frac{\mathrm{2}\mu^{\mathrm{2}} }{\mu^{\mathrm{2}} +\mathrm{1}}\:\:\:…\left({i}\right) \\ $$$$ \\ $$$${center}\:{of}\:{small}\:{circle}\:{B}: \\ $$$${x}_{{B}} ={a}\:\mathrm{cos}\:\theta+{r}\:\mathrm{sin}\:\varphi \\ $$$${y}_{{B}} ={b}\:\mathrm{sin}\:\theta+{r}\:\mathrm{cos}\:\varphi \\ $$$${AB}={R}−{r} \\ $$$$\left({a}\:\mathrm{cos}\:\theta+{r}\:\mathrm{sin}\:\varphi−{R}+{r}\right)^{\mathrm{2}} +\left({b}\:\mathrm{sin}\:\theta+{r}\:\mathrm{cos}\:\varphi\right)^{\mathrm{2}} =\left({R}−{r}\right)^{\mathrm{2}} \\ $$$$\left(\frac{{a}}{{R}}\:\mathrm{cos}\:\theta+\lambda\:\mathrm{sin}\:\varphi−\mathrm{1}+\lambda\right)^{\mathrm{2}} +\left(\frac{{b}}{{R}}\:\mathrm{sin}\:\theta+\lambda\:\mathrm{cos}\:\varphi\right)^{\mathrm{2}} =\left(\mathrm{1}−\lambda\right)^{\mathrm{2}} \\ $$$$\left[\left(\mathrm{2}−\lambda\right)\:\mathrm{cos}\:\theta+\lambda\:\mathrm{sin}\:\varphi−\mathrm{1}+\lambda\right]^{\mathrm{2}} +\left[\sqrt{\left(\mathrm{2}−\lambda\right)\lambda}\:\mathrm{sin}\:\theta+\lambda\:\mathrm{cos}\:\varphi\right]^{\mathrm{2}} =\left(\mathrm{1}−\lambda\right)^{\mathrm{2}} \\ $$$$\left[\left(\mathrm{2}−\lambda\right)\:\mathrm{cos}\:\theta+\frac{\lambda\mu}{\:\sqrt{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\theta}}−\mathrm{1}+\lambda\right]^{\mathrm{2}} +\left[\sqrt{\left(\mathrm{2}−\lambda\right)\lambda}\:\mathrm{sin}\:\theta+\frac{\lambda\:\mathrm{tan}\:\theta}{\:\sqrt{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\theta}}\right]^{\mathrm{2}} =\left(\mathrm{1}−\lambda\right)^{\mathrm{2}} \:\:\:…\left({ii}\right) \\ $$$$\frac{{r}}{{a}}=\frac{\lambda}{\mathrm{2}−\lambda}=\mu^{\mathrm{2}} \\ $$$${i}.{e}.\:{when}\:\mu\:{is}\:{maximum},\:{r}\:{is}\:{also} \\ $$$${maximum}.\:{from}\:\left({ii}\right)\:{we}\:{get} \\ $$$$\mu_{{max}} \approx\mathrm{0}.\mathrm{35355}\:{at}\:\theta\approx\mathrm{1}.\mathrm{047} \\ $$$$\left({see}\:{diagram}\:\mathrm{1}\right) \\ $$$${the}\:{eccentricity}\:{e}=\sqrt{\mathrm{1}−\mu^{\mathrm{2}} }\approx\mathrm{0}.\mathrm{9354} \\ $$

Commented by mr W last updated on 13/Mar/21