Question Number 135543 by 0731619177 last updated on 13/Mar/21

Answered by Olaf last updated on 13/Mar/21
![Ω = ∫_0 ^(π/2) cos(2x)tan((x/2))dx Ω = ∫_0 ^(π/2) ((1−tan^2 x)/(1+tan^2 x))tan((x/2))dx Ω = ∫_0 ^(π/2) ((1−(((2tan(x/2))/(1−tan^2 (x/2))))^2 )/(1+(((2tan(x/2))/(1−tan^2 (x/2))))^2 ))tan((x/2))dx Let t = tan(x/2) Ω = ∫_0 ^1 ((1−(((2t)/(1−t^2 )))^2 )/(1+(((2t)/(1−t^2 )))^2 )) t(((2dt)/(1+t^2 ))) Ω = ∫_0 ^1 (((1−t^2 )^2 −4t^2 )/((1−t^2 )^2 +4t^2 )).((2t)/(1+t^2 )) dt Ω =2 ∫_0 ^1 ((t^4 −6t^2 +1)/(t^4 +2t^2 +1)) .(t/(1+t^2 )) dt Ω =2 ∫_0 ^1 t.((t^4 −6t^2 +1)/((1+t^2 )^3 )) dt Ω =2 ∫_0 ^1 t.(((1+t^2 )^2 −8(1+t^2 )+8)/((1+t^2 )^3 )) dt Ω =2 ∫_0 ^1 ((t/(1+t^2 ))−((8t)/((1+t^2 )^2 ))+((8t)/((1+t^2 )^3 ))) dt Ω =2 [(1/2)ln(1+t^2 )+(4/(1+t^2 ))−(2/((1+t^2 )^2 ))]_0 ^1 Ω = 2[((1/2)ln2+2−(1/2))−(4−2)] Ω = ln2−1 = ln(2/e)](https://www.tinkutara.com/question/Q135547.png)
$$\Omega\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cos}\left(\mathrm{2}{x}\right)\mathrm{tan}\left(\frac{{x}}{\mathrm{2}}\right){dx} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} {x}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} {x}}\mathrm{tan}\left(\frac{{x}}{\mathrm{2}}\right){dx} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}−\left(\frac{\mathrm{2tan}\frac{{x}}{\mathrm{2}}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}\right)^{\mathrm{2}} }{\mathrm{1}+\left(\frac{\mathrm{2tan}\frac{{x}}{\mathrm{2}}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}\right)^{\mathrm{2}} }\mathrm{tan}\left(\frac{{x}}{\mathrm{2}}\right){dx} \\ $$$$\mathrm{Let}\:{t}\:=\:\mathrm{tan}\frac{{x}}{\mathrm{2}} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−\left(\frac{\mathrm{2}{t}}{\mathrm{1}−{t}^{\mathrm{2}} }\right)^{\mathrm{2}} }{\mathrm{1}+\left(\frac{\mathrm{2}{t}}{\mathrm{1}−{t}^{\mathrm{2}} }\right)^{\mathrm{2}} }\:{t}\left(\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\right) \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{4}{t}^{\mathrm{2}} }{\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{4}{t}^{\mathrm{2}} }.\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\:{dt} \\ $$$$\Omega\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}^{\mathrm{4}} −\mathrm{6}{t}^{\mathrm{2}} +\mathrm{1}}{{t}^{\mathrm{4}} +\mathrm{2}{t}^{\mathrm{2}} +\mathrm{1}}\:.\frac{{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\:{dt} \\ $$$$\Omega\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} {t}.\frac{{t}^{\mathrm{4}} −\mathrm{6}{t}^{\mathrm{2}} +\mathrm{1}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{3}} }\:{dt} \\ $$$$\Omega\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} {t}.\frac{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{8}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)+\mathrm{8}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{3}} }\:{dt} \\ $$$$\Omega\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{{t}}{\mathrm{1}+{t}^{\mathrm{2}} }−\frac{\mathrm{8}{t}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }+\frac{\mathrm{8}{t}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{3}} }\right)\:{dt} \\ $$$$\Omega\:=\mathrm{2}\:\left[\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)+\frac{\mathrm{4}}{\mathrm{1}+{t}^{\mathrm{2}} }−\frac{\mathrm{2}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\Omega\:=\:\mathrm{2}\left[\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln2}+\mathrm{2}−\frac{\mathrm{1}}{\mathrm{2}}\right)−\left(\mathrm{4}−\mathrm{2}\right)\right] \\ $$$$\Omega\:=\:\mathrm{ln2}−\mathrm{1}\:=\:\mathrm{ln}\frac{\mathrm{2}}{{e}} \\ $$
Answered by mnjuly1970 last updated on 13/Mar/21
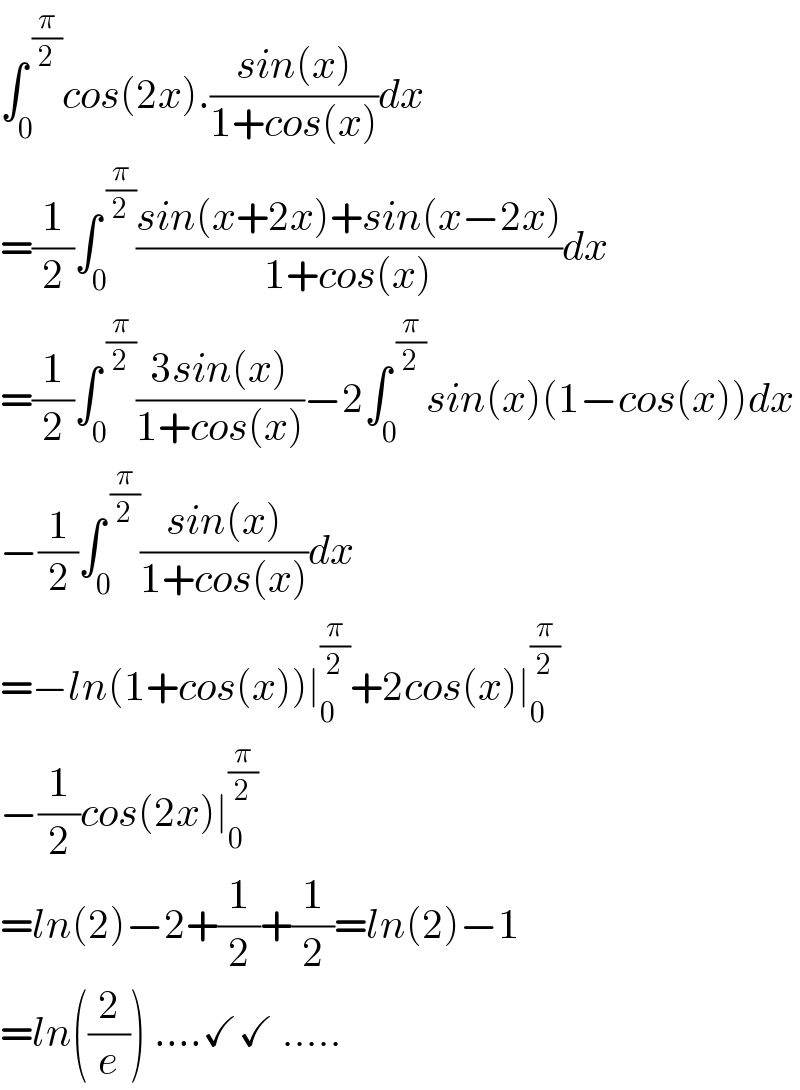
$$\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {cos}\left(\mathrm{2}{x}\right).\frac{{sin}\left({x}\right)}{\mathrm{1}+{cos}\left({x}\right)}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \frac{{sin}\left({x}+\mathrm{2}{x}\right)+{sin}\left({x}−\mathrm{2}{x}\right)}{\mathrm{1}+{cos}\left({x}\right)}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \frac{\mathrm{3}{sin}\left({x}\right)}{\mathrm{1}+{cos}\left({x}\right)}−\mathrm{2}\int_{\mathrm{0}\:} ^{\:\frac{\pi}{\mathrm{2}}} {sin}\left({x}\right)\left(\mathrm{1}−{cos}\left({x}\right)\right){dx} \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \frac{{sin}\left({x}\right)}{\mathrm{1}+{cos}\left({x}\right)}{dx} \\ $$$$=−{ln}\left(\mathrm{1}+{cos}\left({x}\right)\right)\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} +\mathrm{2}{cos}\left({x}\right)\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}{cos}\left(\mathrm{2}{x}\right)\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$={ln}\left(\mathrm{2}\right)−\mathrm{2}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}={ln}\left(\mathrm{2}\right)−\mathrm{1} \\ $$$$={ln}\left(\frac{\mathrm{2}}{{e}}\right)\:….\checkmark\checkmark\:….. \\ $$
