Menu Close

Question-135653

Tinku Tara 0 Comments
Pin




Question Number 135653 by I want to learn more last updated on 14/Mar/21
Commented by mr W last updated on 14/Mar/21
question is wrong. just check again.
$${question}\:{is}\:{wrong}.\:{just}\:{check}\:{again}. \\ $$
Commented by I want to learn more last updated on 14/Mar/21
That is the question sir, and what makes it wrong sir please.
$$\mathrm{That}\:\mathrm{is}\:\mathrm{the}\:\mathrm{question}\:\mathrm{sir},\:\mathrm{and}\:\mathrm{what}\:\mathrm{makes}\:\mathrm{it}\:\mathrm{wrong}\:\mathrm{sir}\:\mathrm{please}. \\ $$
Commented by mr W last updated on 14/Mar/21
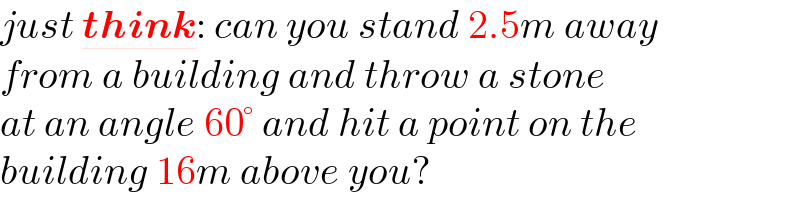
just think: can you stand 2.5m away from a building and throw a stone at an angle 60° and hit a point on the building 16m above you?
$${just}\:\underline{\boldsymbol{{think}}}:\:{can}\:{you}\:{stand}\:\mathrm{2}.\mathrm{5}{m}\:{away} \\ $$$${from}\:{a}\:{building}\:{and}\:{throw}\:{a}\:{stone} \\ $$$${at}\:{an}\:{angle}\:\mathrm{60}°\:{and}\:{hit}\:{a}\:{point}\:{on}\:{the} \\ $$$${building}\:\mathrm{16}{m}\:{above}\:{you}? \\ $$
Commented by mr W last updated on 14/Mar/21
Commented by I want to learn more last updated on 14/Mar/21
Alright sir, i understand.
$$\mathrm{Alright}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{understand}. \\ $$
Commented by I want to learn more last updated on 14/Mar/21
I get it clearly sir.
$$\mathrm{I}\:\mathrm{get}\:\mathrm{it}\:\mathrm{clearly}\:\mathrm{sir}.\: \\ $$
Commented by I want to learn more last updated on 14/Mar/21
Sir please help me correct the value, i want to see the procedure and diagram for such question
$$\mathrm{Sir}\:\mathrm{please}\:\mathrm{help}\:\mathrm{me}\:\mathrm{correct}\:\mathrm{the}\:\mathrm{value},\:\:\mathrm{i}\:\mathrm{want}\:\mathrm{to}\:\mathrm{see}\:\mathrm{the}\:\mathrm{procedure} \\ $$$$\mathrm{and}\:\mathrm{diagram}\:\mathrm{for}\:\mathrm{such}\:\mathrm{question} \\ $$
Commented by mr W last updated on 14/Mar/21
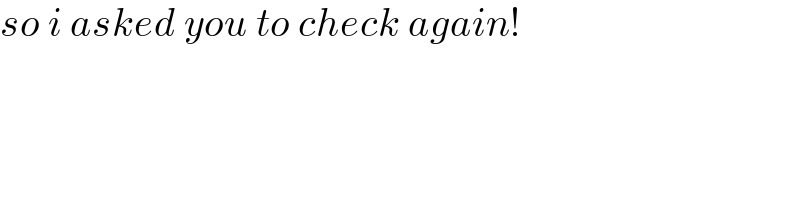
so i asked you to check again!
$${so}\:{i}\:{asked}\:{you}\:{to}\:{check}\:{again}! \\ $$
Commented by I want to learn more last updated on 14/Mar/21
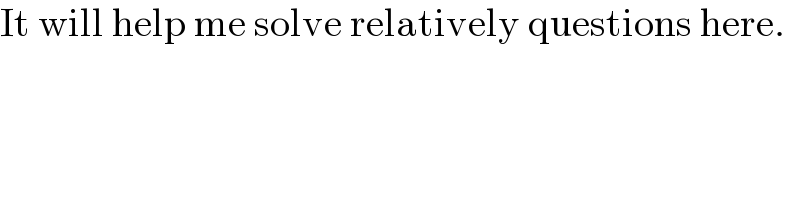
It will help me solve relatively questions here.
$$\mathrm{It}\:\mathrm{will}\:\mathrm{help}\:\mathrm{me}\:\mathrm{solve}\:\mathrm{relatively}\:\mathrm{questions}\:\mathrm{here}. \\ $$
Answered by mr W last updated on 15/Mar/21
Commented by mr W last updated on 15/Mar/21
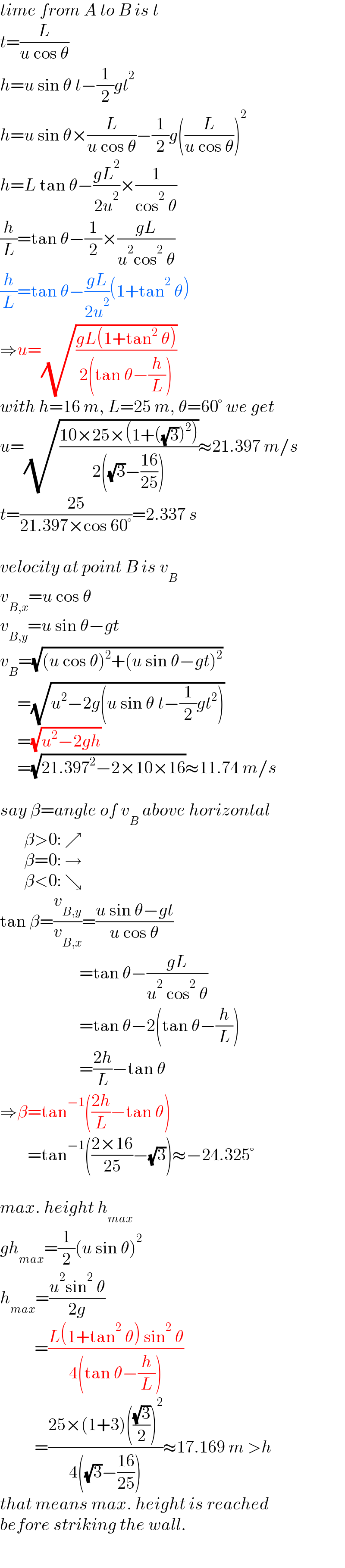
time from A to B is t t=(L/(u cos θ)) h=u sin θ t−(1/2)gt^2 h=u sin θ×(L/(u cos θ))−(1/2)g((L/(u cos θ)))^2 h=L tan θ−((gL^2 )/(2u^2 ))×(1/(cos^2 θ)) (h/L)=tan θ−(1/2)×((gL)/(u^2 cos^2 θ)) (h/L)=tan θ−((gL)/(2u^2 ))(1+tan^2 θ) ⇒u=(√((gL(1+tan^2 θ))/(2(tan θ−(h/L))))) with h=16 m, L=25 m, θ=60° we get u=(√((10×25×(1+((√3))^2 ))/(2((√3)−((16)/(25))))))≈21.397 m/s t=((25)/(21.397×cos 60°))=2.337 s velocity at point B is v_B v_(B,x) =u cos θ v_(B,y) =u sin θ−gt v_B =(√((u cos θ)^2 +(u sin θ−gt)^2 )) =(√(u^2 −2g(u sin θ t−(1/2)gt^2 ))) =(√(u^2 −2gh)) =(√(21.397^2 −2×10×16))≈11.74 m/s say β=angle of v_B above horizontal β>0: ↗ β=0: → β<0: ↘ tan β=(v_(B,y) /v_(B,x) )=((u sin θ−gt)/(u cos θ)) =tan θ−((gL)/(u^2 cos^2 θ)) =tan θ−2(tan θ−(h/L)) =((2h)/L)−tan θ ⇒β=tan^(−1) (((2h)/L)−tan θ) =tan^(−1) (((2×16)/(25))−(√3))≈−24.325° max. height h_(max) gh_(max) =(1/2)(u sin θ)^2 h_(max) =((u^2 sin^2 θ)/(2g)) =((L(1+tan^2 θ) sin^2 θ)/(4(tan θ−(h/L)))) =((25×(1+3)(((√3)/2))^2 )/(4((√3)−((16)/(25)))))≈17.169 m >h that means max. height is reached before striking the wall.
$${time}\:{from}\:{A}\:{to}\:{B}\:{is}\:{t} \\ $$$${t}=\frac{{L}}{{u}\:\mathrm{cos}\:\theta} \\ $$$${h}={u}\:\mathrm{sin}\:\theta\:{t}−\frac{\mathrm{1}}{\mathrm{2}}{gt}^{\mathrm{2}} \\ $$$${h}={u}\:\mathrm{sin}\:\theta×\frac{{L}}{{u}\:\mathrm{cos}\:\theta}−\frac{\mathrm{1}}{\mathrm{2}}{g}\left(\frac{{L}}{{u}\:\mathrm{cos}\:\theta}\right)^{\mathrm{2}} \\ $$$${h}={L}\:\mathrm{tan}\:\theta−\frac{{gL}^{\mathrm{2}} }{\mathrm{2}{u}^{\mathrm{2}} }×\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \:\theta} \\ $$$$\frac{{h}}{{L}}=\mathrm{tan}\:\theta−\frac{\mathrm{1}}{\mathrm{2}}×\frac{{gL}}{{u}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta} \\ $$$$\frac{{h}}{{L}}=\mathrm{tan}\:\theta−\frac{{gL}}{\mathrm{2}{u}^{\mathrm{2}} }\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta\right) \\ $$$$\Rightarrow{u}=\sqrt{\frac{{gL}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta\right)}{\mathrm{2}\left(\mathrm{tan}\:\theta−\frac{{h}}{{L}}\right)}} \\ $$$${with}\:{h}=\mathrm{16}\:{m},\:{L}=\mathrm{25}\:{m},\:\theta=\mathrm{60}°\:{we}\:{get} \\ $$$${u}=\sqrt{\frac{\mathrm{10}×\mathrm{25}×\left(\mathrm{1}+\left(\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \right)}{\mathrm{2}\left(\sqrt{\mathrm{3}}−\frac{\mathrm{16}}{\mathrm{25}}\right)}}\approx\mathrm{21}.\mathrm{397}\:{m}/{s} \\ $$$${t}=\frac{\mathrm{25}}{\mathrm{21}.\mathrm{397}×\mathrm{cos}\:\mathrm{60}°}=\mathrm{2}.\mathrm{337}\:{s} \\ $$$$ \\ $$$${velocity}\:{at}\:{point}\:{B}\:{is}\:{v}_{{B}} \\ $$$${v}_{{B},{x}} ={u}\:\mathrm{cos}\:\theta \\ $$$${v}_{{B},{y}} ={u}\:\mathrm{sin}\:\theta−{gt} \\ $$$${v}_{{B}} =\sqrt{\left({u}\:\mathrm{cos}\:\theta\right)^{\mathrm{2}} +\left({u}\:\mathrm{sin}\:\theta−{gt}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:=\sqrt{{u}^{\mathrm{2}} −\mathrm{2}{g}\left({u}\:\mathrm{sin}\:\theta\:{t}−\frac{\mathrm{1}}{\mathrm{2}}{gt}^{\mathrm{2}} \right)} \\ $$$$\:\:\:\:\:=\sqrt{{u}^{\mathrm{2}} −\mathrm{2}{gh}} \\ $$$$\:\:\:\:\:=\sqrt{\mathrm{21}.\mathrm{397}^{\mathrm{2}} −\mathrm{2}×\mathrm{10}×\mathrm{16}}\approx\mathrm{11}.\mathrm{74}\:{m}/{s} \\ $$$$ \\ $$$${say}\:\beta={angle}\:{of}\:{v}_{{B}} \:{above}\:{horizontal} \\ $$$$\:\:\:\:\:\:\:\beta>\mathrm{0}:\:\nearrow \\ $$$$\:\:\:\:\:\:\:\beta=\mathrm{0}:\:\rightarrow \\ $$$$\:\:\:\:\:\:\:\beta<\mathrm{0}:\:\searrow \\ $$$$\mathrm{tan}\:\beta=\frac{{v}_{{B},{y}} }{{v}_{{B},{x}} }=\frac{{u}\:\mathrm{sin}\:\theta−{gt}}{{u}\:\mathrm{cos}\:\theta} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{tan}\:\theta−\frac{{gL}}{{u}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\theta} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{tan}\:\theta−\mathrm{2}\left(\mathrm{tan}\:\theta−\frac{{h}}{{L}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{2}{h}}{{L}}−\mathrm{tan}\:\theta \\ $$$$\Rightarrow\beta=\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}{h}}{{L}}−\mathrm{tan}\:\theta\right) \\ $$$$\:\:\:\:\:\:\:\:=\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}×\mathrm{16}}{\mathrm{25}}−\sqrt{\mathrm{3}}\right)\approx−\mathrm{24}.\mathrm{325}° \\ $$$$ \\ $$$${max}.\:{height}\:{h}_{{max}} \\ $$$${gh}_{{max}} =\frac{\mathrm{1}}{\mathrm{2}}\left({u}\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} \\ $$$${h}_{{max}} =\frac{{u}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}{\mathrm{2}{g}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{{L}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta\right)\:\mathrm{sin}^{\mathrm{2}} \:\theta}{\mathrm{4}\left(\mathrm{tan}\:\theta−\frac{{h}}{{L}}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{25}×\left(\mathrm{1}+\mathrm{3}\right)\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{4}\left(\sqrt{\mathrm{3}}−\frac{\mathrm{16}}{\mathrm{25}}\right)}\approx\mathrm{17}.\mathrm{169}\:{m}\:>{h} \\ $$$${that}\:{means}\:{max}.\:{height}\:{is}\:{reached} \\ $$$${before}\:{striking}\:{the}\:{wall}. \\ $$
Commented by mr W last updated on 15/Mar/21
Commented by I want to learn more last updated on 15/Mar/21
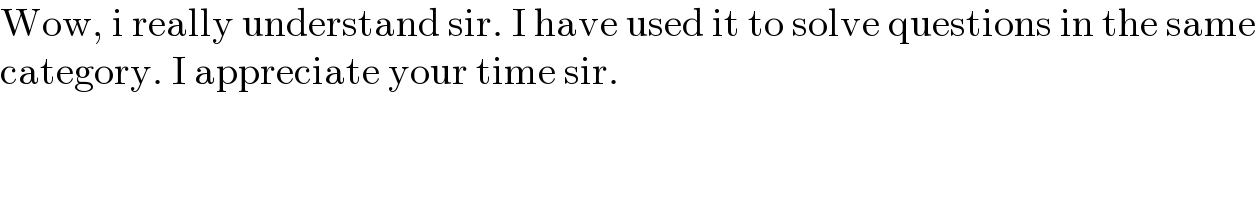
Wow, i really understand sir. I have used it to solve questions in the same category. I appreciate your time sir.
$$\mathrm{Wow},\:\mathrm{i}\:\mathrm{really}\:\mathrm{understand}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{have}\:\mathrm{used}\:\mathrm{it}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{questions}\:\mathrm{in}\:\mathrm{the}\:\mathrm{same} \\ $$$$\mathrm{category}.\:\mathrm{I}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir}.\: \\ $$
Commented by Tawa11 last updated on 14/Sep/21
nice
$$\mathrm{nice} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *