Question Number 135709 by Algoritm last updated on 15/Mar/21
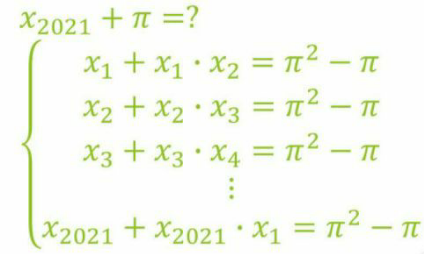
Commented by mr W last updated on 15/Mar/21
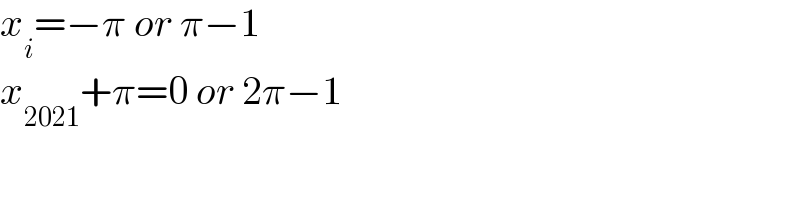
$${x}_{{i}} =−\pi\:{or}\:\pi−\mathrm{1} \\ $$$${x}_{\mathrm{2021}} +\pi=\mathrm{0}\:{or}\:\mathrm{2}\pi−\mathrm{1} \\ $$
Answered by Olaf last updated on 15/Mar/21
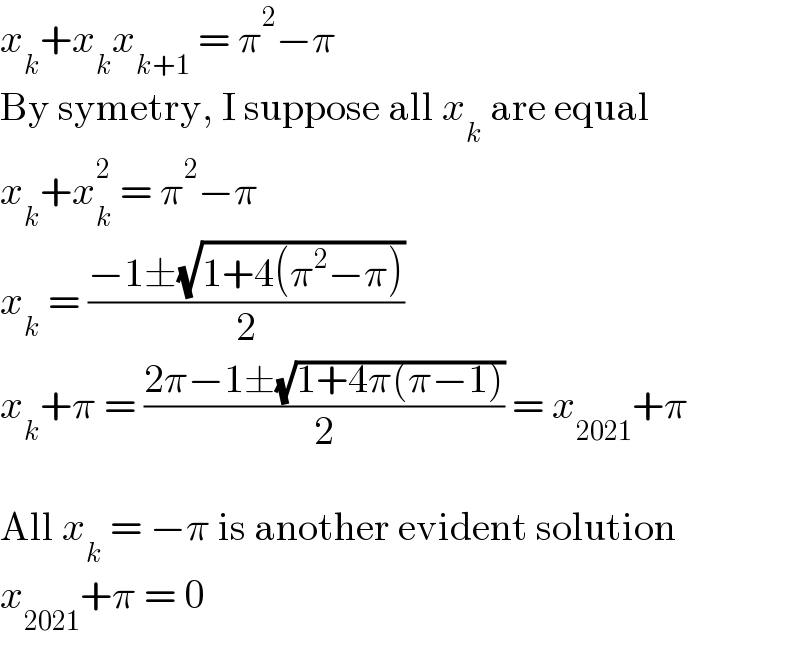
$${x}_{{k}} +{x}_{{k}} {x}_{{k}+\mathrm{1}} \:=\:\pi^{\mathrm{2}} −\pi \\ $$$$\mathrm{By}\:\mathrm{symetry},\:\mathrm{I}\:\mathrm{suppose}\:\mathrm{all}\:{x}_{{k}} \:\mathrm{are}\:\mathrm{equal} \\ $$$${x}_{{k}} +{x}_{{k}} ^{\mathrm{2}} \:=\:\pi^{\mathrm{2}} −\pi \\ $$$${x}_{{k}} \:=\:\frac{−\mathrm{1}\pm\sqrt{\mathrm{1}+\mathrm{4}\left(\pi^{\mathrm{2}} −\pi\right)}}{\mathrm{2}} \\ $$$${x}_{{k}} +\pi\:=\:\frac{\mathrm{2}\pi−\mathrm{1}\pm\sqrt{\mathrm{1}+\mathrm{4}\pi\left(\pi−\mathrm{1}\right)}}{\mathrm{2}}\:=\:{x}_{\mathrm{2021}} +\pi \\ $$$$ \\ $$$$\mathrm{All}\:{x}_{{k}} \:=\:−\pi\:\mathrm{is}\:\mathrm{another}\:\mathrm{evident}\:\mathrm{solution} \\ $$$${x}_{\mathrm{2021}} +\pi\:=\:\mathrm{0} \\ $$
Commented by mr W last updated on 15/Mar/21
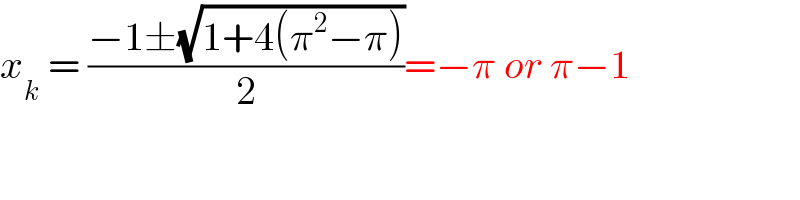
$${x}_{{k}} \:=\:\frac{−\mathrm{1}\pm\sqrt{\mathrm{1}+\mathrm{4}\left(\pi^{\mathrm{2}} −\pi\right)}}{\mathrm{2}}=−\pi\:{or}\:\pi−\mathrm{1} \\ $$
