Question-135712

Question Number 135712 by Dwaipayan Shikari last updated on 15/Mar/21

Commented by Dwaipayan Shikari last updated on 15/Mar/21

$${Smaller}\:{circle}\:{has}\:{half}\:{of}\:{the}\:{radius}\:{of}\:{the}\:{larger}\:{circle}. \\ $$$${Prove}\:{that},\:{irrespective}\:{of}\:{any}\:{position}\:{oc}\:{the}\:{smaller}\:{circle}\: \\ $$$${that}\:{blue}\:{point}\:{will}\:{always}\:{stay}\:{on}\:{the}\:{diametre}\:{of}\:{that}\: \\ $$$${larger}\:{circle} \\ $$

Answered by mr W last updated on 15/Mar/21

Commented by mr W last updated on 15/Mar/21

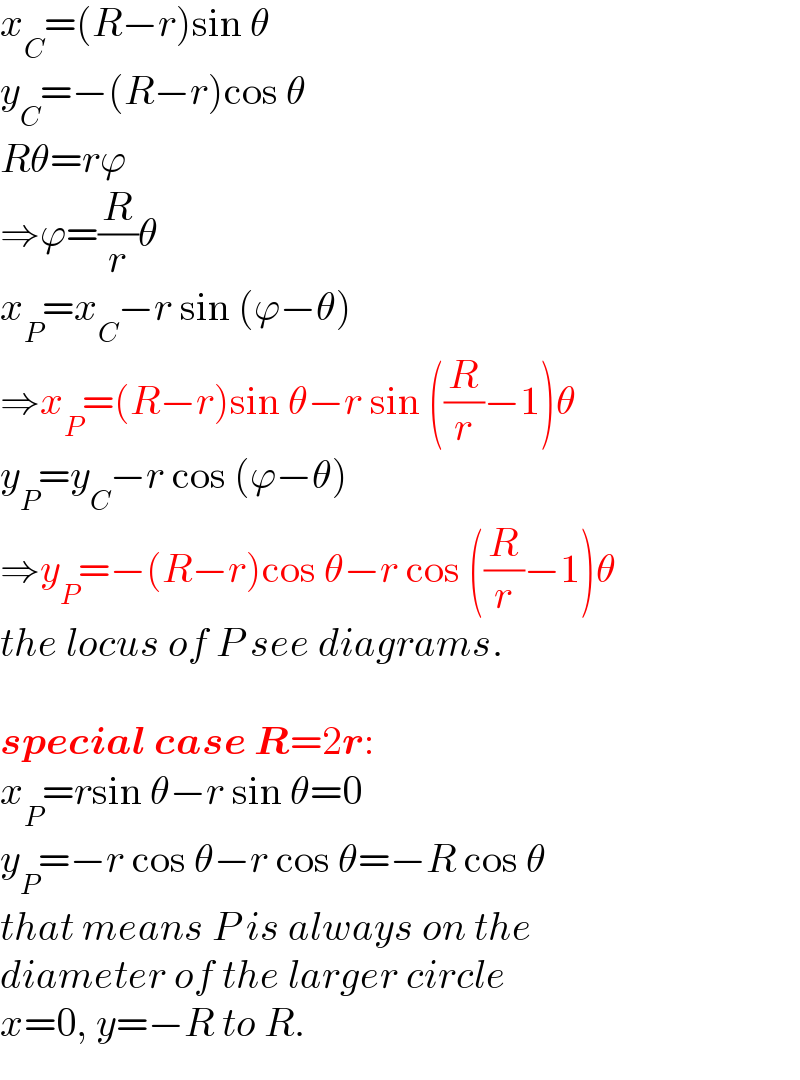
x_C =(R−r)sin θ y_C =−(R−r)cos θ Rθ=rϕ ⇒ϕ=(R/r)θ x_P =x_C −r sin (ϕ−θ) ⇒x_P =(R−r)sin θ−r sin ((R/r)−1)θ y_P =y_C −r cos (ϕ−θ) ⇒y_P =−(R−r)cos θ−r cos ((R/r)−1)θ the locus of P see diagrams. special case R=2r: x_P =rsin θ−r sin θ=0 y_P =−r cos θ−r cos θ=−R cos θ that means P is always on the diameter of the larger circle x=0, y=−R to R.

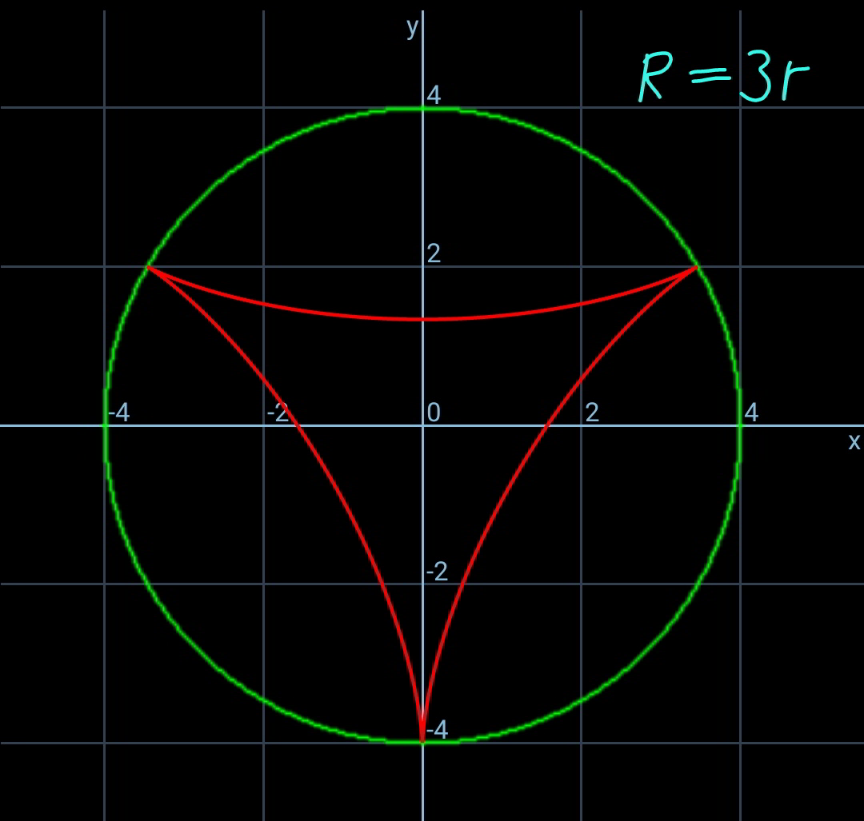
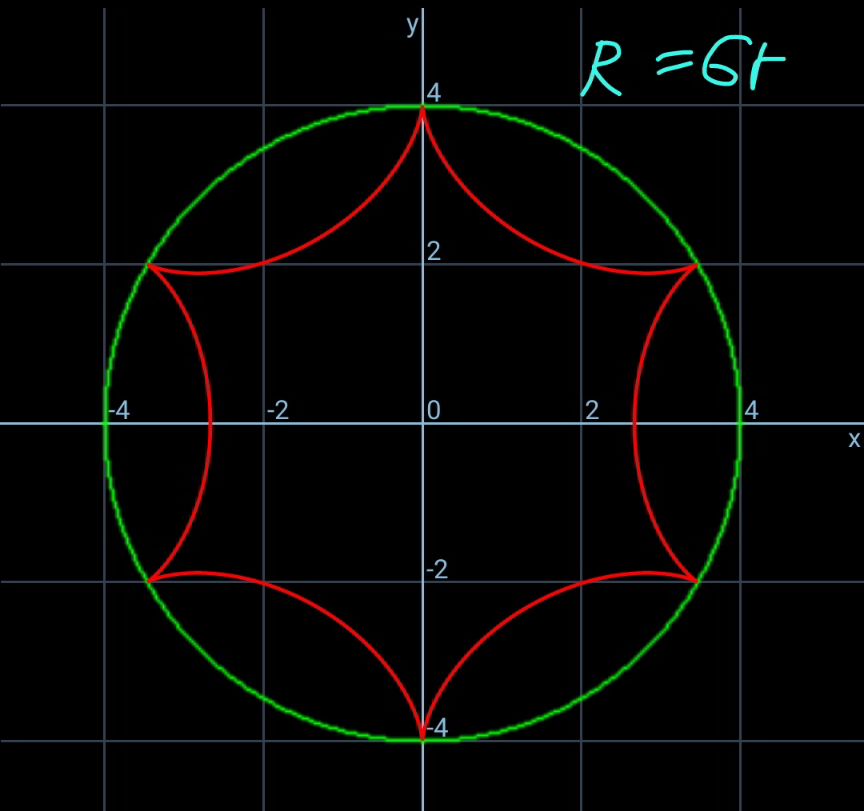
$${x}_{{C}} =\left({R}−{r}\right)\mathrm{sin}\:\theta \\ $$$${y}_{{C}} =−\left({R}−{r}\right)\mathrm{cos}\:\theta \\ $$$${R}\theta={r}\varphi \\ $$$$\Rightarrow\varphi=\frac{{R}}{{r}}\theta \\ $$$${x}_{{P}} ={x}_{{C}} −{r}\:\mathrm{sin}\:\left(\varphi−\theta\right) \\ $$$$\Rightarrow{x}_{{P}} =\left({R}−{r}\right)\mathrm{sin}\:\theta−{r}\:\mathrm{sin}\:\left(\frac{{R}}{{r}}−\mathrm{1}\right)\theta \\ $$$${y}_{{P}} ={y}_{{C}} −{r}\:\mathrm{cos}\:\left(\varphi−\theta\right) \\ $$$$\Rightarrow{y}_{{P}} =−\left({R}−{r}\right)\mathrm{cos}\:\theta−{r}\:\mathrm{cos}\:\left(\frac{{R}}{{r}}−\mathrm{1}\right)\theta \\ $$$${the}\:{locus}\:{of}\:{P}\:{see}\:{diagrams}. \\ $$$$ \\ $$$$\boldsymbol{{special}}\:\boldsymbol{{case}}\:\boldsymbol{{R}}=\mathrm{2}\boldsymbol{{r}}: \\ $$$${x}_{{P}} ={r}\mathrm{sin}\:\theta−{r}\:\mathrm{sin}\:\theta=\mathrm{0} \\ $$$${y}_{{P}} =−{r}\:\mathrm{cos}\:\theta−{r}\:\mathrm{cos}\:\theta=−{R}\:\mathrm{cos}\:\theta \\ $$$${that}\:{means}\:{P}\:{is}\:{always}\:{on}\:{the} \\ $$$${diameter}\:{of}\:{the}\:{larger}\:{circle} \\ $$$${x}=\mathrm{0},\:{y}=−{R}\:{to}\:{R}. \\ $$

Commented by mr W last updated on 15/Mar/21