Menu Close

Question-135742

Tinku Tara 0 Comments
Pin




Question Number 135742 by mohssinee last updated on 15/Mar/21
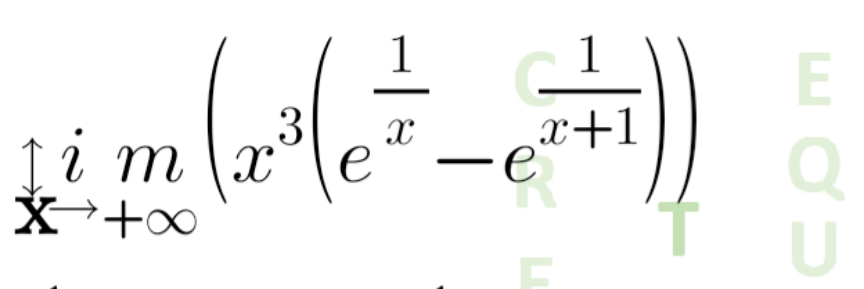
Commented by mohssinee last updated on 15/Mar/21
help me !
$${help}\:{me}\:! \\ $$
Answered by mathmax by abdo last updated on 15/Mar/21
e^(1/x) ∼1+(1/x) and e^(1/(x+1)) ∼1+(1/(x+1)) ⇒e^(1/x) −e^(1/(x+1)) ∼(1/x)−(1/(x+1))=(1/(x^2 +x)) ⇒ x^3 (e^(1/x) −e^(1/(x+1)) )∼(x^3 /(x^2 +x))∼x ⇒lim_(x→+∞) x^3 (e^(1/x) −e^(1/(x+1)) )=+∞ another method put (1/x)=t (sot→0^+ ) ⇒x=(1/t) ⇒x+1 =(1/t)+1=((t+1)/t) ⇒f(x)=(1/t^3 )(e^t −e^(t/(t+1)) ) we have e^t ∼1+t +(t^2 /2) e^(t/(t+1)) ∼1+(t/(t+1)) +(t^2 /(2(t+1)^2 )) ⇒e^t −e^(t/(t+1)) ∼t+(t^2 /2)−(t/(t+1))−(t^2 /(2(t+1)^2 )) =(t^2 /(t+1))+(t^2 /2)(1−(1/(t^2 +2t+1)))=(t^2 /(t+1))+(t^2 /2)(((t^2 +2t)/(t^2 +2t+1))) ⇒ ((e^t −e^(t/(t+1)) )/t^3 )∼(1/(t(t+1)))+(1/(2t))(((t^2 +2t)/(t^2 +2t+1)))=(1/(t(t+1)))+((t+2)/(2(t^2 +2t+1))) lim_(t→0^+ ) (1/(t(t+1)))=+∞ ⇒lim_(x→+∞) f(x)=+∞
$$\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}} \sim\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}}\:\:\mathrm{and}\:\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}} \sim\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\:\Rightarrow\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}} −\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}} \sim\frac{\mathrm{1}}{\mathrm{x}}−\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}}\:\Rightarrow \\ $$$$\mathrm{x}^{\mathrm{3}} \left(\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}} −\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}} \right)\sim\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}}\sim\mathrm{x}\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{x}^{\mathrm{3}} \left(\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}} −\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}} \right)=+\infty \\ $$$$\mathrm{another}\:\mathrm{method}\:\mathrm{put}\:\frac{\mathrm{1}}{\mathrm{x}}=\mathrm{t}\:\left(\mathrm{sot}\rightarrow\mathrm{0}^{+} \right)\:\Rightarrow\mathrm{x}=\frac{\mathrm{1}}{\mathrm{t}}\:\Rightarrow\mathrm{x}+\mathrm{1}\:=\frac{\mathrm{1}}{\mathrm{t}}+\mathrm{1}=\frac{\mathrm{t}+\mathrm{1}}{\mathrm{t}} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{3}} }\left(\mathrm{e}^{\mathrm{t}} −\mathrm{e}^{\frac{\mathrm{t}}{\mathrm{t}+\mathrm{1}}} \right)\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{e}^{\mathrm{t}} \:\sim\mathrm{1}+\mathrm{t}\:+\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\mathrm{e}^{\frac{\mathrm{t}}{\mathrm{t}+\mathrm{1}}} \:\sim\mathrm{1}+\frac{\mathrm{t}}{\mathrm{t}+\mathrm{1}}\:+\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow\mathrm{e}^{\mathrm{t}} −\mathrm{e}^{\frac{\mathrm{t}}{\mathrm{t}+\mathrm{1}}} \:\sim\mathrm{t}+\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{t}}{\mathrm{t}+\mathrm{1}}−\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{t}+\mathrm{1}}+\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} +\mathrm{2t}+\mathrm{1}}\right)=\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{t}+\mathrm{1}}+\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}\left(\frac{\mathrm{t}^{\mathrm{2}} \:+\mathrm{2t}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{2t}+\mathrm{1}}\right)\:\Rightarrow \\ $$$$\frac{\mathrm{e}^{\mathrm{t}} −\mathrm{e}^{\frac{\mathrm{t}}{\mathrm{t}+\mathrm{1}}} }{\mathrm{t}^{\mathrm{3}} }\sim\frac{\mathrm{1}}{\mathrm{t}\left(\mathrm{t}+\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{2t}}\left(\frac{\mathrm{t}^{\mathrm{2}} \:+\mathrm{2t}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{2t}+\mathrm{1}}\right)=\frac{\mathrm{1}}{\mathrm{t}\left(\mathrm{t}+\mathrm{1}\right)}+\frac{\mathrm{t}+\mathrm{2}}{\mathrm{2}\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{2t}+\mathrm{1}\right)} \\ $$$$\mathrm{lim}_{\mathrm{t}\rightarrow\mathrm{0}^{+} } \:\:\:\frac{\mathrm{1}}{\mathrm{t}\left(\mathrm{t}+\mathrm{1}\right)}=+\infty\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{f}\left(\mathrm{x}\right)=+\infty \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *