Question Number 135800 by benjo_mathlover last updated on 16/Mar/21

Answered by Olaf last updated on 16/Mar/21
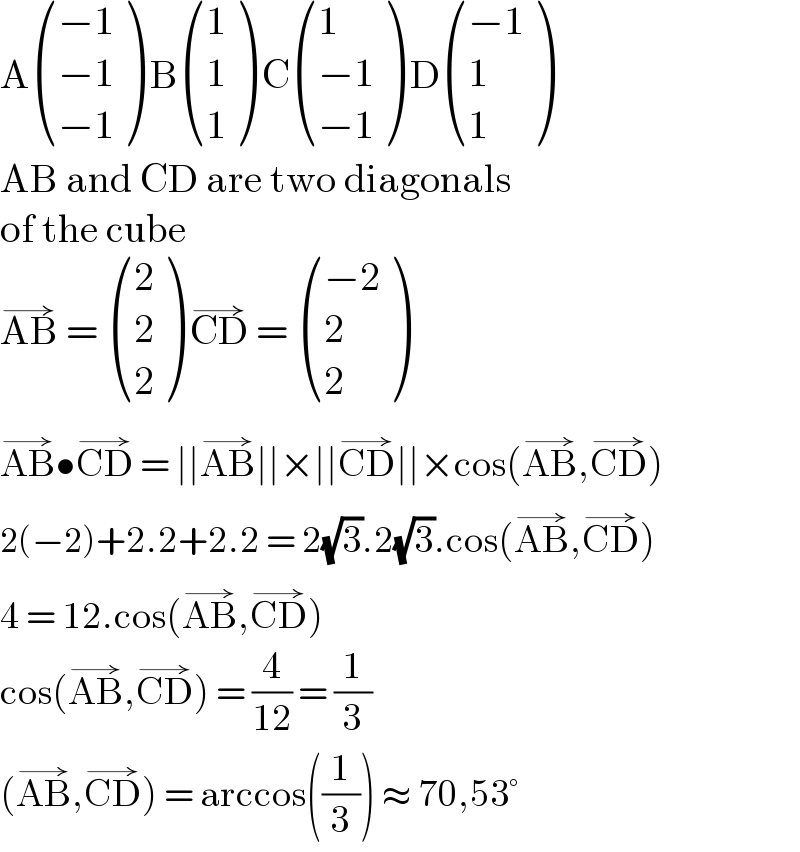
$$\mathrm{A}\begin{pmatrix}{−\mathrm{1}}\\{−\mathrm{1}}\\{−\mathrm{1}}\end{pmatrix}\:\mathrm{B}\begin{pmatrix}{\mathrm{1}}\\{\mathrm{1}}\\{\mathrm{1}}\end{pmatrix}\:\mathrm{C}\begin{pmatrix}{\mathrm{1}}\\{−\mathrm{1}}\\{−\mathrm{1}}\end{pmatrix}\:\mathrm{D}\begin{pmatrix}{−\mathrm{1}}\\{\mathrm{1}}\\{\mathrm{1}}\end{pmatrix} \\ $$$$\mathrm{AB}\:\mathrm{and}\:\mathrm{CD}\:\mathrm{are}\:\mathrm{two}\:\mathrm{diagonals} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{cube} \\ $$$$\overset{\rightarrow} {\mathrm{AB}}\:=\:\begin{pmatrix}{\mathrm{2}}\\{\mathrm{2}}\\{\mathrm{2}}\end{pmatrix}\:\overset{\rightarrow} {\mathrm{CD}}\:=\:\begin{pmatrix}{−\mathrm{2}}\\{\mathrm{2}}\\{\mathrm{2}}\end{pmatrix} \\ $$$$\overset{\rightarrow} {\mathrm{AB}}\bullet\overset{\rightarrow} {\mathrm{CD}}\:=\:\mid\mid\overset{\rightarrow} {\mathrm{AB}}\mid\mid×\mid\mid\overset{\rightarrow} {\mathrm{CD}}\mid\mid×\mathrm{cos}\left(\overset{\rightarrow} {\mathrm{AB}},\overset{\rightarrow} {\mathrm{CD}}\right) \\ $$$$\mathrm{2}\left(−\mathrm{2}\right)+\mathrm{2}.\mathrm{2}+\mathrm{2}.\mathrm{2}\:=\:\mathrm{2}\sqrt{\mathrm{3}}.\mathrm{2}\sqrt{\mathrm{3}}.\mathrm{cos}\left(\overset{\rightarrow} {\mathrm{AB}},\overset{\rightarrow} {\mathrm{CD}}\right) \\ $$$$\mathrm{4}\:=\:\mathrm{12}.\mathrm{cos}\left(\overset{\rightarrow} {\mathrm{AB}},\overset{\rightarrow} {\mathrm{CD}}\right) \\ $$$$\mathrm{cos}\left(\overset{\rightarrow} {\mathrm{AB}},\overset{\rightarrow} {\mathrm{CD}}\right)\:=\:\frac{\mathrm{4}}{\mathrm{12}}\:=\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\left(\overset{\rightarrow} {\mathrm{AB}},\overset{\rightarrow} {\mathrm{CD}}\right)\:=\:\mathrm{arccos}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\:\approx\:\mathrm{70},\mathrm{53}° \\ $$
Answered by mr W last updated on 16/Mar/21
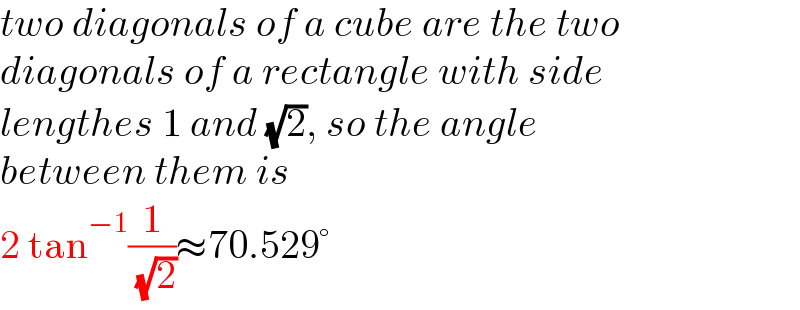
$${two}\:{diagonals}\:{of}\:{a}\:{cube}\:{are}\:{the}\:{two} \\ $$$${diagonals}\:{of}\:{a}\:{rectangle}\:{with}\:{side} \\ $$$${lengthes}\:\mathrm{1}\:{and}\:\sqrt{\mathrm{2}},\:{so}\:{the}\:{angle} \\ $$$${between}\:{them}\:{is} \\ $$$$\mathrm{2}\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\approx\mathrm{70}.\mathrm{529}° \\ $$
Commented by mr W last updated on 16/Mar/21

