Question Number 135816 by ShiimiGee last updated on 16/Mar/21

Commented by ShiimiGee last updated on 16/Mar/21

$$ \\ $$
Commented by liberty last updated on 16/Mar/21
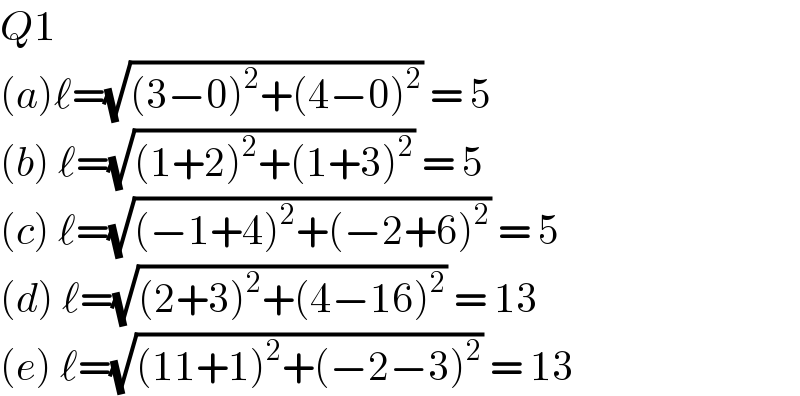
$${Q}\mathrm{1} \\ $$$$\left({a}\right)\ell=\sqrt{\left(\mathrm{3}−\mathrm{0}\right)^{\mathrm{2}} +\left(\mathrm{4}−\mathrm{0}\right)^{\mathrm{2}} }\:=\:\mathrm{5} \\ $$$$\left({b}\right)\:\ell=\sqrt{\left(\mathrm{1}+\mathrm{2}\right)^{\mathrm{2}} +\left(\mathrm{1}+\mathrm{3}\right)^{\mathrm{2}} }\:=\:\mathrm{5} \\ $$$$\left({c}\right)\:\ell=\sqrt{\left(−\mathrm{1}+\mathrm{4}\right)^{\mathrm{2}} +\left(−\mathrm{2}+\mathrm{6}\right)^{\mathrm{2}} }\:=\:\mathrm{5} \\ $$$$\left({d}\right)\:\ell=\sqrt{\left(\mathrm{2}+\mathrm{3}\right)^{\mathrm{2}} +\left(\mathrm{4}−\mathrm{16}\right)^{\mathrm{2}} }\:=\:\mathrm{13} \\ $$$$\left({e}\right)\:\ell=\sqrt{\left(\mathrm{11}+\mathrm{1}\right)^{\mathrm{2}} +\left(−\mathrm{2}−\mathrm{3}\right)^{\mathrm{2}} }\:=\:\mathrm{13} \\ $$
Commented by EDWIN88 last updated on 16/Mar/21

$$\mathrm{Q2}. \\ $$$$\left(\mathrm{i}\right)\:\begin{cases}{\mathrm{x}=\mathrm{rcos}\:\alpha}\\{\mathrm{y}=\mathrm{rsin}\:\alpha}\end{cases}\:\Rightarrow\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \:=\:\mathrm{r}^{\mathrm{2}} \\ $$$$\:\therefore\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} −\mathrm{2y}=\mathrm{0}\:\Rightarrow\mathrm{r}^{\mathrm{2}} −\mathrm{2r}\:\mathrm{sin}\:\alpha\:=\:\mathrm{0} \\ $$$$\left(\mathrm{ii}\right)\:\mathrm{r}^{\mathrm{2}} \:\mathrm{sin}\:^{\mathrm{2}} \alpha\:=\:\mathrm{4}{a}\left({a}−{r}\:\mathrm{cos}\:\alpha\right) \\ $$$$\:\:\:\:\mathrm{r}^{\mathrm{2}} \:\mathrm{sin}\:^{\mathrm{2}} \alpha\:+\mathrm{4}{ar}\:\mathrm{cos}\:\alpha\:=\:\mathrm{4}{a}^{\mathrm{2}} \\ $$
