Menu Close

Question-135818

Tinku Tara 0 Comments
Pin




Question Number 135818 by mr W last updated on 16/Mar/21
Commented by mr W last updated on 16/Mar/21
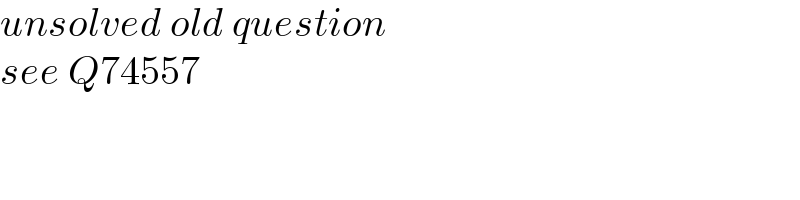
unsolved old question see Q74557
$${unsolved}\:{old}\:{question} \\ $$$${see}\:{Q}\mathrm{74557} \\ $$
Answered by mr W last updated on 16/Mar/21
Commented by mr W last updated on 17/Mar/21
Commented by mr W last updated on 21/Mar/21
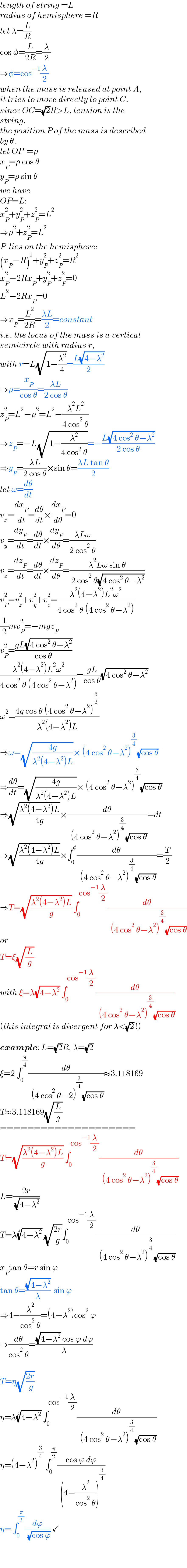
length of string =L radius of hemisphere =R let λ=(L/R) cos φ=(L/(2R))=(λ/2) ⇒φ=cos^(−1) (λ/2) when the mass is released at point A, it tries to move directly to point C. since OC=(√2)R>L, tension is the string. the position P of the mass is described by θ. let OP ′=ρ x_P =ρ cos θ y_P =ρ sin θ we have OP=L: x_P ^2 +y_P ^2 +z_P ^2 =L^2 ⇒ρ^2 +z_P ^2 =L^2 P lies on the hemisphere: (x_P −R)^2 +y_P ^2 +z_P ^2 =R^2 x_P ^2 −2Rx_P +y_P ^2 +z_P ^2 =0 L^2 −2Rx_P =0 ⇒x_P =(L^2 /(2R))=((λL)/2)=constant i.e. the locus of the mass is a vertical semicircle with radius r, with r=L(√(1−(λ^2 /4)))=((L(√(4−λ^2 )))/2) ⇒ρ=(x_P /(cos θ))=((λL)/(2 cos θ)) z_P ^2 =L^2 −ρ^2 =L^2 −((λ^2 L^2 )/(4 cos^2 θ)) ⇒z_P =−L(√(1−(λ^2 /(4 cos^2 θ))))=−((L(√(4 cos^2 θ−λ^2 )))/(2 cos θ)) ⇒y_P =((λL)/(2 cos θ))×sin θ=((λL tan θ)/2) let ω=(dθ/dt) v_x =(dx_P /dt)=(dθ/dt)×(dx_P /dθ)=0 v_y =(dy_P /dt)=(dθ/dt)×(dy_P /dθ)=((λLω)/(2 cos^2 θ)) v_z =(dz_P /dt)=(dθ/dt)×(dz_P /dθ)=((λ^2 Lω sin θ)/( 2 cos^2 θ(√(4 cos^2 θ−λ^2 )))) v_P ^2 =v_x ^2 +v_y ^2 +v_z ^2 =((λ^2 (4−λ^2 )L^2 ω^2 )/(4 cos^2 θ (4 cos^2 θ−λ^2 ))) (1/2)mv_P ^2 =−mgz_P v_P ^2 =((gL(√(4 cos^2 θ−λ^2 )))/(cos θ)) ((λ^2 (4−λ^2 )L^2 ω^2 )/(4 cos^2 θ (4 cos^2 θ−λ^2 )))=((gL)/(cos θ))(√(4 cos^2 θ−λ^2 )) ω^2 =((4g cos θ (4 cos^2 θ−λ^2 )^(3/2) )/(λ^2 (4−λ^2 )L)) ⇒ω=(√((4g)/(λ^2 (4−λ^2 )L)))× (4 cos^2 θ−λ^2 )^(3/4) (√(cos θ)) ⇒(dθ/dt)=(√((4g)/(λ^2 (4−λ^2 )L)))× (4 cos^2 θ−λ^2 )^(3/4) (√(cos θ)) ⇒(√((λ^2 (4−λ^2 )L)/(4g)))×(dθ/( (4 cos^2 θ−λ^2 )^(3/4) (√(cos θ))))=dt ⇒(√((λ^2 (4−λ^2 )L)/(4g)))×∫_0 ^φ (dθ/( (4 cos^2 θ−λ^2 )^(3/4) (√(cos θ))))=(T/2) ⇒T=(√((λ^2 (4−λ^2 )L)/g)) ∫_0 ^(cos^(−1) (λ/2)) (dθ/( (4 cos^2 θ−λ^2 )^(3/4) (√(cos θ)))) or T=ξ(√(L/g)) with ξ=λ(√(4−λ^2 )) ∫_0 ^(cos^(−1) (λ/2)) (dθ/( (4 cos^2 θ−λ^2 )^(3/4) (√(cos θ)))) (this integral is divergent for λ<(√2) !) example: L=(√2)R, λ=(√2) ξ=2 ∫_0 ^(π/4) (dθ/( (4 cos^2 θ−2)^(3/4) (√(cos θ))))≈3.118169 T≈3.118169(√(L/g)) ==================== T=(√((λ^2 (4−λ^2 )L)/g)) ∫_0 ^(cos^(−1) (λ/2)) (dθ/( (4 cos^2 θ−λ^2 )^(3/4) (√(cos θ)))) L=((2r)/( (√(4−λ^2 )))) T=λ((4−λ^2 ))^(1/4) (√((2r)/g))∫_0 ^(cos^(−1) (λ/2)) (dθ/( (4 cos^2 θ−λ^2 )^(3/4) (√(cos θ)))) x_P tan θ=r sin ϕ tan θ=((√(4−λ^2 ))/λ) sin ϕ ⇒4−(λ^2 /(cos^2 θ))=(4−λ^2 )cos^2 ϕ ⇒(dθ/(cos^2 θ))=(((√(4−λ^2 )) cos ϕ dϕ)/λ) T=η(√((2r)/( g))) η=λ((4−λ^2 ))^(1/4) ∫_0 ^(cos^(−1) (λ/2)) (dθ/( (4 cos^2 θ−λ^2 )^(3/4) (√(cos θ)))) η=(4−λ^2 )^(3/4) ∫_0 ^(π/2) ((cos ϕ dϕ)/( (4−(λ^2 /(cos^2 θ)))^(3/4) )) η= ∫_0 ^(π/2) (dϕ/( (√(cos ϕ)))) ✓
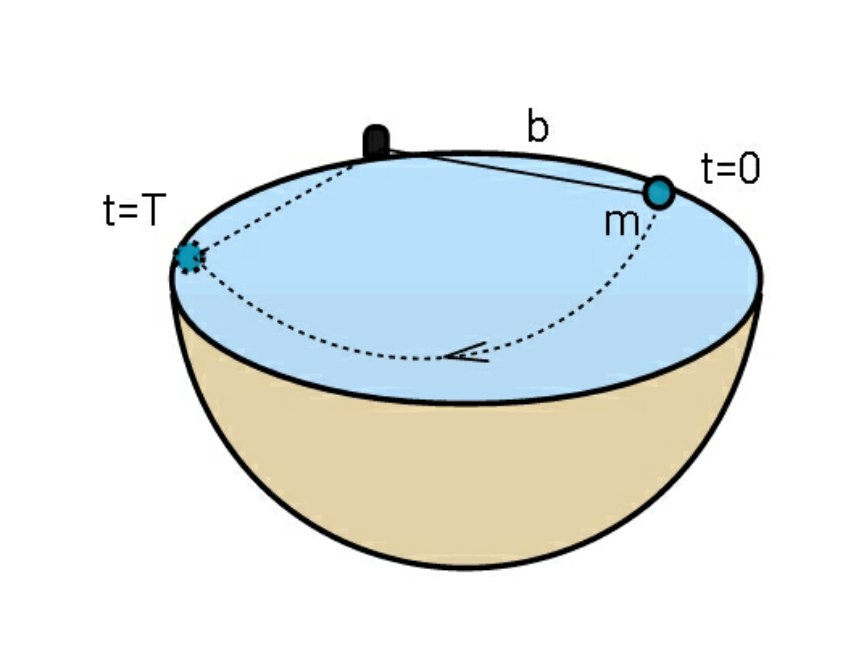
$${length}\:{of}\:{string}\:={L} \\ $$$${radius}\:{of}\:{hemisphere}\:={R} \\ $$$${let}\:\lambda=\frac{{L}}{{R}} \\ $$$$\mathrm{cos}\:\phi=\frac{{L}}{\mathrm{2}{R}}=\frac{\lambda}{\mathrm{2}} \\ $$$$\Rightarrow\phi=\mathrm{cos}^{−\mathrm{1}} \frac{\lambda}{\mathrm{2}} \\ $$$${when}\:{the}\:{mass}\:{is}\:{released}\:{at}\:{point}\:{A}, \\ $$$${it}\:{tries}\:{to}\:{move}\:{directly}\:{to}\:{point}\:{C}. \\ $$$${since}\:{OC}=\sqrt{\mathrm{2}}{R}>{L},\:{tension}\:{is}\:{the} \\ $$$${string}. \\ $$$${the}\:{position}\:{P}\:{of}\:{the}\:{mass}\:{is}\:{described} \\ $$$${by}\:\theta. \\ $$$${let}\:{OP}\:'=\rho \\ $$$${x}_{{P}} =\rho\:\mathrm{cos}\:\theta \\ $$$${y}_{{P}} =\rho\:\mathrm{sin}\:\theta \\ $$$${we}\:{have} \\ $$$${OP}={L}: \\ $$$${x}_{{P}} ^{\mathrm{2}} +{y}_{{P}} ^{\mathrm{2}} +{z}_{{P}} ^{\mathrm{2}} ={L}^{\mathrm{2}} \\ $$$$\Rightarrow\rho^{\mathrm{2}} +{z}_{{P}} ^{\mathrm{2}} ={L}^{\mathrm{2}} \\ $$$${P}\:\:{lies}\:{on}\:{the}\:{hemisphere}: \\ $$$$\left({x}_{{P}} −{R}\right)^{\mathrm{2}} +{y}_{{P}} ^{\mathrm{2}} +{z}_{{P}} ^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$${x}_{{P}} ^{\mathrm{2}} −\mathrm{2}{Rx}_{{P}} +{y}_{{P}} ^{\mathrm{2}} +{z}_{{P}} ^{\mathrm{2}} =\mathrm{0} \\ $$$${L}^{\mathrm{2}} −\mathrm{2}{Rx}_{{P}} =\mathrm{0} \\ $$$$\Rightarrow{x}_{{P}} =\frac{{L}^{\mathrm{2}} }{\mathrm{2}{R}}=\frac{\lambda{L}}{\mathrm{2}}={constant} \\ $$$${i}.{e}.\:{the}\:{locus}\:{of}\:{the}\:{mass}\:{is}\:{a}\:{vertical} \\ $$$${semicircle}\:{with}\:{radius}\:{r},\: \\ $$$${with}\:{r}={L}\sqrt{\mathrm{1}−\frac{\lambda^{\mathrm{2}} }{\mathrm{4}}}=\frac{{L}\sqrt{\mathrm{4}−\lambda^{\mathrm{2}} }}{\mathrm{2}} \\ $$$$\Rightarrow\rho=\frac{{x}_{{P}} }{\mathrm{cos}\:\theta}=\frac{\lambda{L}}{\mathrm{2}\:\mathrm{cos}\:\theta} \\ $$$${z}_{{P}} ^{\mathrm{2}} ={L}^{\mathrm{2}} −\rho^{\mathrm{2}} ={L}^{\mathrm{2}} −\frac{\lambda^{\mathrm{2}} {L}^{\mathrm{2}} }{\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\theta} \\ $$$$\Rightarrow{z}_{{P}} =−{L}\sqrt{\mathrm{1}−\frac{\lambda^{\mathrm{2}} }{\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\theta}}=−\frac{{L}\sqrt{\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\theta−\lambda^{\mathrm{2}} }}{\mathrm{2}\:\mathrm{cos}\:\theta} \\ $$$$\Rightarrow{y}_{{P}} =\frac{\lambda{L}}{\mathrm{2}\:\mathrm{cos}\:\theta}×\mathrm{sin}\:\theta=\frac{\lambda{L}\:\mathrm{tan}\:\theta}{\mathrm{2}} \\ $$$${let}\:\omega=\frac{{d}\theta}{{dt}} \\ $$$${v}_{{x}} =\frac{{dx}_{{P}} }{{dt}}=\frac{{d}\theta}{{dt}}×\frac{{dx}_{{P}} }{{d}\theta}=\mathrm{0} \\ $$$${v}_{{y}} =\frac{{dy}_{{P}} }{{dt}}=\frac{{d}\theta}{{dt}}×\frac{{dy}_{{P}} }{{d}\theta}=\frac{\lambda{L}\omega}{\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\theta} \\ $$$${v}_{{z}} =\frac{{dz}_{{P}} }{{dt}}=\frac{{d}\theta}{{dt}}×\frac{{dz}_{{P}} }{{d}\theta}=\frac{\lambda^{\mathrm{2}} {L}\omega\:\mathrm{sin}\:\theta}{\:\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\theta\sqrt{\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\theta−\lambda^{\mathrm{2}} }} \\ $$$${v}_{{P}} ^{\mathrm{2}} ={v}_{{x}} ^{\mathrm{2}} +{v}_{{y}} ^{\mathrm{2}} +{v}_{{z}} ^{\mathrm{2}} =\frac{\lambda^{\mathrm{2}} \left(\mathrm{4}−\lambda^{\mathrm{2}} \right){L}^{\mathrm{2}} \omega^{\mathrm{2}} }{\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\theta\:\left(\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\theta−\lambda^{\mathrm{2}} \right)} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{mv}_{{P}} ^{\mathrm{2}} =−{mgz}_{{P}} \\ $$$${v}_{{P}} ^{\mathrm{2}} =\frac{{gL}\sqrt{\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\theta−\lambda^{\mathrm{2}} }}{\mathrm{cos}\:\theta} \\ $$$$\frac{\lambda^{\mathrm{2}} \left(\mathrm{4}−\lambda^{\mathrm{2}} \right){L}^{\mathrm{2}} \omega^{\mathrm{2}} }{\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\theta\:\left(\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\theta−\lambda^{\mathrm{2}} \right)}=\frac{{gL}}{\mathrm{cos}\:\theta}\sqrt{\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\theta−\lambda^{\mathrm{2}} } \\ $$$$\omega^{\mathrm{2}} =\frac{\mathrm{4}{g}\:\mathrm{cos}\:\theta\:\left(\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\theta−\lambda^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{\lambda^{\mathrm{2}} \left(\mathrm{4}−\lambda^{\mathrm{2}} \right){L}} \\ $$$$\Rightarrow\omega=\sqrt{\frac{\mathrm{4}{g}}{\lambda^{\mathrm{2}} \left(\mathrm{4}−\lambda^{\mathrm{2}} \right){L}}}×\:\left(\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\theta−\lambda^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{4}}} \sqrt{\mathrm{cos}\:\theta} \\ $$$$\Rightarrow\frac{{d}\theta}{{dt}}=\sqrt{\frac{\mathrm{4}{g}}{\lambda^{\mathrm{2}} \left(\mathrm{4}−\lambda^{\mathrm{2}} \right){L}}}×\:\left(\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\theta−\lambda^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{4}}} \sqrt{\mathrm{cos}\:\theta} \\ $$$$\Rightarrow\sqrt{\frac{\lambda^{\mathrm{2}} \left(\mathrm{4}−\lambda^{\mathrm{2}} \right){L}}{\mathrm{4}{g}}}×\frac{{d}\theta}{\:\:\left(\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\theta−\lambda^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{4}}} \sqrt{\mathrm{cos}\:\theta}}={dt} \\ $$$$\Rightarrow\sqrt{\frac{\lambda^{\mathrm{2}} \left(\mathrm{4}−\lambda^{\mathrm{2}} \right){L}}{\mathrm{4}{g}}}×\int_{\mathrm{0}} ^{\phi} \frac{{d}\theta}{\:\:\left(\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\theta−\lambda^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{4}}} \sqrt{\mathrm{cos}\:\theta}}=\frac{{T}}{\mathrm{2}} \\ $$$$\Rightarrow{T}=\sqrt{\frac{\lambda^{\mathrm{2}} \left(\mathrm{4}−\lambda^{\mathrm{2}} \right){L}}{{g}}}\:\int_{\mathrm{0}} ^{\mathrm{cos}^{−\mathrm{1}} \frac{\lambda}{\mathrm{2}}} \frac{{d}\theta}{\:\:\left(\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\theta−\lambda^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{4}}} \sqrt{\mathrm{cos}\:\theta}} \\ $$$${or} \\ $$$${T}=\xi\sqrt{\frac{{L}}{{g}}} \\ $$$${with}\:\xi=\lambda\sqrt{\mathrm{4}−\lambda^{\mathrm{2}} }\:\int_{\mathrm{0}} ^{\mathrm{cos}^{−\mathrm{1}} \frac{\lambda}{\mathrm{2}}} \frac{{d}\theta}{\:\:\left(\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\theta−\lambda^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{4}}} \sqrt{\mathrm{cos}\:\theta}} \\ $$$$\left({this}\:{integral}\:{is}\:{divergent}\:{for}\:\lambda<\sqrt{\mathrm{2}}\:!\right) \\ $$$$ \\ $$$$\boldsymbol{{example}}:\:{L}=\sqrt{\mathrm{2}}{R},\:\lambda=\sqrt{\mathrm{2}} \\ $$$$\xi=\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{d}\theta}{\:\:\left(\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{2}\right)^{\frac{\mathrm{3}}{\mathrm{4}}} \sqrt{\mathrm{cos}\:\theta}}\approx\mathrm{3}.\mathrm{118169} \\ $$$${T}\approx\mathrm{3}.\mathrm{118169}\sqrt{\frac{{L}}{{g}}} \\ $$$$==================== \\ $$$${T}=\sqrt{\frac{\lambda^{\mathrm{2}} \left(\mathrm{4}−\lambda^{\mathrm{2}} \right){L}}{{g}}}\:\int_{\mathrm{0}} ^{\mathrm{cos}^{−\mathrm{1}} \frac{\lambda}{\mathrm{2}}} \frac{{d}\theta}{\:\:\left(\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\theta−\lambda^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{4}}} \sqrt{\mathrm{cos}\:\theta}} \\ $$$${L}=\frac{\mathrm{2}{r}}{\:\sqrt{\mathrm{4}−\lambda^{\mathrm{2}} }} \\ $$$${T}=\lambda\sqrt[{\mathrm{4}}]{\mathrm{4}−\lambda^{\mathrm{2}} }\:\sqrt{\frac{\mathrm{2}{r}}{{g}}}\int_{\mathrm{0}} ^{\mathrm{cos}^{−\mathrm{1}} \frac{\lambda}{\mathrm{2}}} \frac{{d}\theta}{\:\:\left(\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\theta−\lambda^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{4}}} \sqrt{\mathrm{cos}\:\theta}} \\ $$$${x}_{{P}} \mathrm{tan}\:\theta={r}\:\mathrm{sin}\:\varphi \\ $$$$\mathrm{tan}\:\theta=\frac{\sqrt{\mathrm{4}−\lambda^{\mathrm{2}} }}{\lambda}\:\:\mathrm{sin}\:\varphi \\ $$$$\Rightarrow\mathrm{4}−\frac{\lambda^{\mathrm{2}} }{\mathrm{cos}^{\mathrm{2}} \:\theta}=\left(\mathrm{4}−\lambda^{\mathrm{2}} \right)\mathrm{cos}^{\mathrm{2}} \:\varphi \\ $$$$\Rightarrow\frac{{d}\theta}{\mathrm{cos}^{\mathrm{2}} \:\theta}=\frac{\sqrt{\mathrm{4}−\lambda^{\mathrm{2}} }\:\mathrm{cos}\:\varphi\:{d}\varphi}{\lambda} \\ $$$$ \\ $$$${T}=\eta\sqrt{\frac{\mathrm{2}{r}}{\:{g}}} \\ $$$$\eta=\lambda\sqrt[{\mathrm{4}}]{\mathrm{4}−\lambda^{\mathrm{2}} }\:\int_{\mathrm{0}} ^{\mathrm{cos}^{−\mathrm{1}} \frac{\lambda}{\mathrm{2}}} \frac{{d}\theta}{\:\:\left(\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\theta−\lambda^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{4}}} \sqrt{\mathrm{cos}\:\theta}} \\ $$$$\eta=\left(\mathrm{4}−\lambda^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{4}}} \:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{cos}\:\varphi\:{d}\varphi}{\:\:\left(\mathrm{4}−\frac{\lambda^{\mathrm{2}} }{\mathrm{cos}^{\mathrm{2}} \:\theta}\right)^{\frac{\mathrm{3}}{\mathrm{4}}} } \\ $$$$\eta=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{d}\varphi}{\:\:\sqrt{\mathrm{cos}\:\varphi}}\:\checkmark \\ $$
Commented by mr W last updated on 17/Mar/21
Commented by mr W last updated on 17/Mar/21
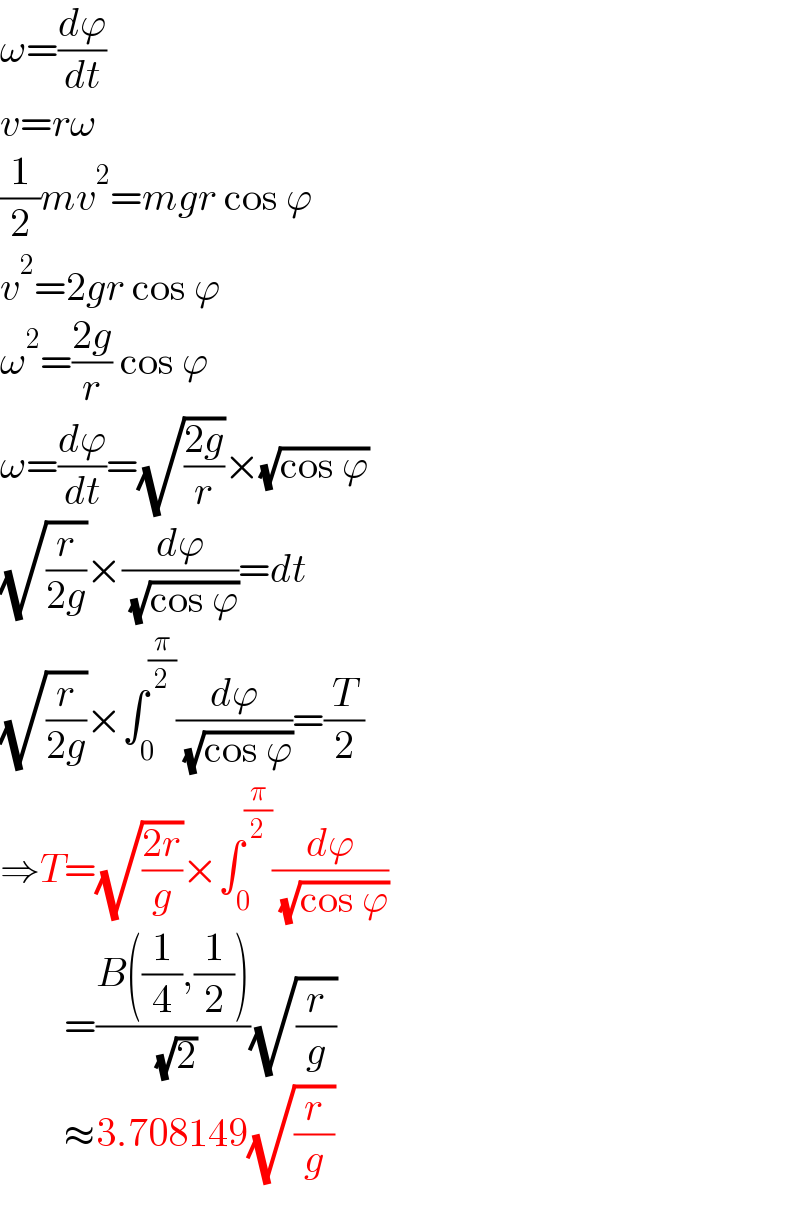
ω=(dϕ/dt) v=rω (1/2)mv^2 =mgr cos ϕ v^2 =2gr cos ϕ ω^2 =((2g)/r) cos ϕ ω=(dϕ/dt)=(√((2g)/r))×(√(cos ϕ)) (√(r/(2g)))×(dϕ/( (√(cos ϕ))))=dt (√(r/(2g)))×∫_0 ^(π/2) (dϕ/( (√(cos ϕ))))=(T/2) ⇒T=(√((2r)/g))×∫_0 ^(π/2) (dϕ/( (√(cos ϕ)))) =((B((1/4),(1/2)))/( (√2)))(√(r/g)) ≈3.708149(√(r/g))
$$\omega=\frac{{d}\varphi}{{dt}} \\ $$$${v}={r}\omega \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{mv}^{\mathrm{2}} ={mgr}\:\mathrm{cos}\:\varphi \\ $$$${v}^{\mathrm{2}} =\mathrm{2}{gr}\:\mathrm{cos}\:\varphi \\ $$$$\omega^{\mathrm{2}} =\frac{\mathrm{2}{g}}{{r}}\:\mathrm{cos}\:\varphi \\ $$$$\omega=\frac{{d}\varphi}{{dt}}=\sqrt{\frac{\mathrm{2}{g}}{{r}}}×\sqrt{\mathrm{cos}\:\varphi} \\ $$$$\sqrt{\frac{{r}}{\mathrm{2}{g}}}×\frac{{d}\varphi}{\:\sqrt{\mathrm{cos}\:\varphi}}={dt} \\ $$$$\sqrt{\frac{{r}}{\mathrm{2}{g}}}×\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{d}\varphi}{\:\sqrt{\mathrm{cos}\:\varphi}}=\frac{{T}}{\mathrm{2}} \\ $$$$\Rightarrow{T}=\sqrt{\frac{\mathrm{2}{r}}{{g}}}×\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{d}\varphi}{\:\sqrt{\mathrm{cos}\:\varphi}} \\ $$$$\:\:\:\:\:\:\:\:=\frac{{B}\left(\frac{\mathrm{1}}{\mathrm{4}},\frac{\mathrm{1}}{\mathrm{2}}\right)}{\:\sqrt{\mathrm{2}}}\sqrt{\frac{{r}}{{g}}} \\ $$$$\:\:\:\:\:\:\:\:\approx\mathrm{3}.\mathrm{708149}\sqrt{\frac{{r}}{{g}}} \\ $$
Commented by mr W last updated on 17/Mar/21
applying this for r=L(√(1−(λ^2 /4))) we get T≈3.708149(1−(λ^2 /4))^(1/4) (√(L/g)) with λ=(L/R) examples: λ=(√2): T≈3.118169 ✓ λ=1: T≈3.450821 λ=(1/2): T≈3.648799
$${applying}\:{this}\:{for}\:{r}={L}\sqrt{\mathrm{1}−\frac{\lambda^{\mathrm{2}} }{\mathrm{4}}}\:{we}\:{get} \\ $$$${T}\approx\mathrm{3}.\mathrm{708149}\left(\mathrm{1}−\frac{\lambda^{\mathrm{2}} }{\mathrm{4}}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} \sqrt{\frac{{L}}{{g}}} \\ $$$${with}\:\lambda=\frac{{L}}{{R}} \\ $$$${examples}: \\ $$$$\lambda=\sqrt{\mathrm{2}}:\:\:\:{T}\approx\mathrm{3}.\mathrm{118169}\:\checkmark \\ $$$$\lambda=\mathrm{1}:\:\:\:\:\:\:{T}\approx\mathrm{3}.\mathrm{450821} \\ $$$$\lambda=\frac{\mathrm{1}}{\mathrm{2}}:\:\:\:\:{T}\approx\mathrm{3}.\mathrm{648799} \\ $$
Commented by ajfour last updated on 17/Mar/21
Thank you, Sir, looks great, shall try to follow as soon as i get well, since yesterday i m down in fever..
$${Thank}\:{you},\:{Sir},\:{looks}\:{great}, \\ $$$${shall}\:{try}\:{to}\:{follow}\:{as}\:{soon}\:{as}\:{i} \\ $$$${get}\:{well},\:{since}\:{yesterday}\:{i}\:{m} \\ $$$${down}\:{in}\:{fever}.. \\ $$
Commented by mr W last updated on 17/Mar/21
sorry to hear that sir, wish you′ll get well soon!
$${sorry}\:{to}\:{hear}\:{that}\:{sir},\:{wish}\:{you}'{ll} \\ $$$${get}\:{well}\:{soon}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *