Question Number 135838 by abdurehime last updated on 16/Mar/21
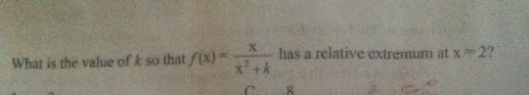
Answered by liberty last updated on 16/Mar/21

$${f}\left({x}\right)=\:\frac{{x}}{{x}^{\mathrm{2}} +{k}}\:\Rightarrow\mathrm{ln}\:{y}\:=\:\mathrm{ln}\:{x}−\mathrm{ln}\:\left({x}^{\mathrm{2}} +{k}\right) \\ $$$$\:\frac{{y}'}{{y}}\:=\:\frac{\mathrm{1}}{{x}}−\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +{k}} \\ $$$$\frac{{y}'}{{y}}\:=\:\frac{{k}−{x}^{\mathrm{2}} }{{x}\left({x}^{\mathrm{2}} +{k}\right)}\:;\:{y}'=\frac{{x}}{\left({x}^{\mathrm{2}} +{k}\right)}.\left(\frac{{k}−{x}^{\mathrm{2}} }{{x}\left({x}^{\mathrm{2}} +{k}\right)}\right) \\ $$$${y}'=\:\frac{{k}−{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} +{k}\right)^{\mathrm{2}} }\:=\:\mathrm{0} \\ $$$${we}\:{get}\:{critical}\:{point}\:{x}=\pm\sqrt{{k}} \\ $$$$\:\begin{array}{|c|c|c|c|}{{interval}}&\hline{{sign}}\\{{x}<−\sqrt{{k}}}&\hline{−}\\{−\sqrt{{k}}<{x}<\sqrt{{k}}}&\hline{+}\\{{x}\:>\sqrt{{k}}}&\hline{−}\\\hline\end{array} \\ $$$${we}\:{get}\:{maximum}\:{value} \\ $$$${when}\:{x}\:=\:\sqrt{{k}}\:=\:\mathrm{2}\:\Rightarrow{k}\:=\:\mathrm{4} \\ $$
