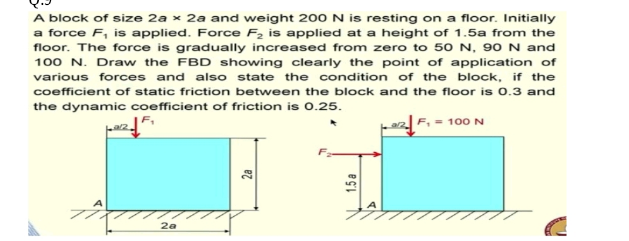
Question Number 136137 by BHOOPENDRA last updated on 19/Mar/21
Answered by mr W last updated on 19/Mar/21
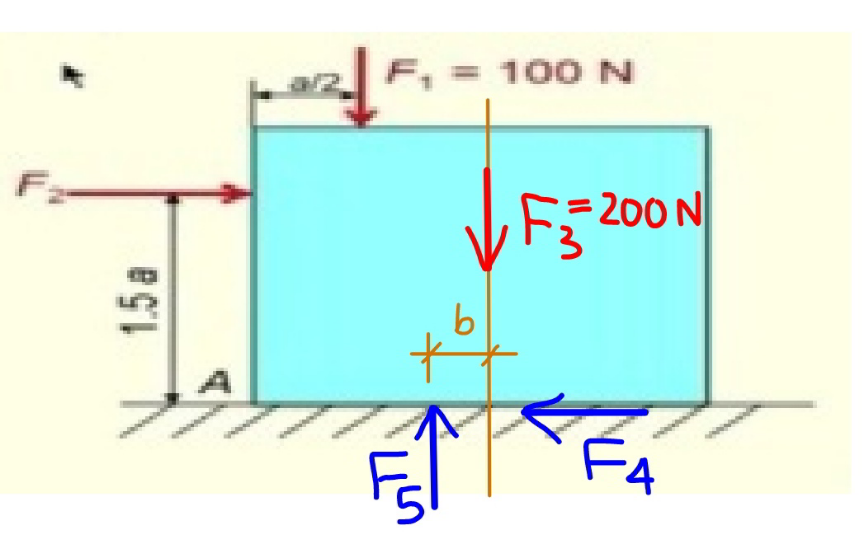
Commented by mr W last updated on 19/Mar/21
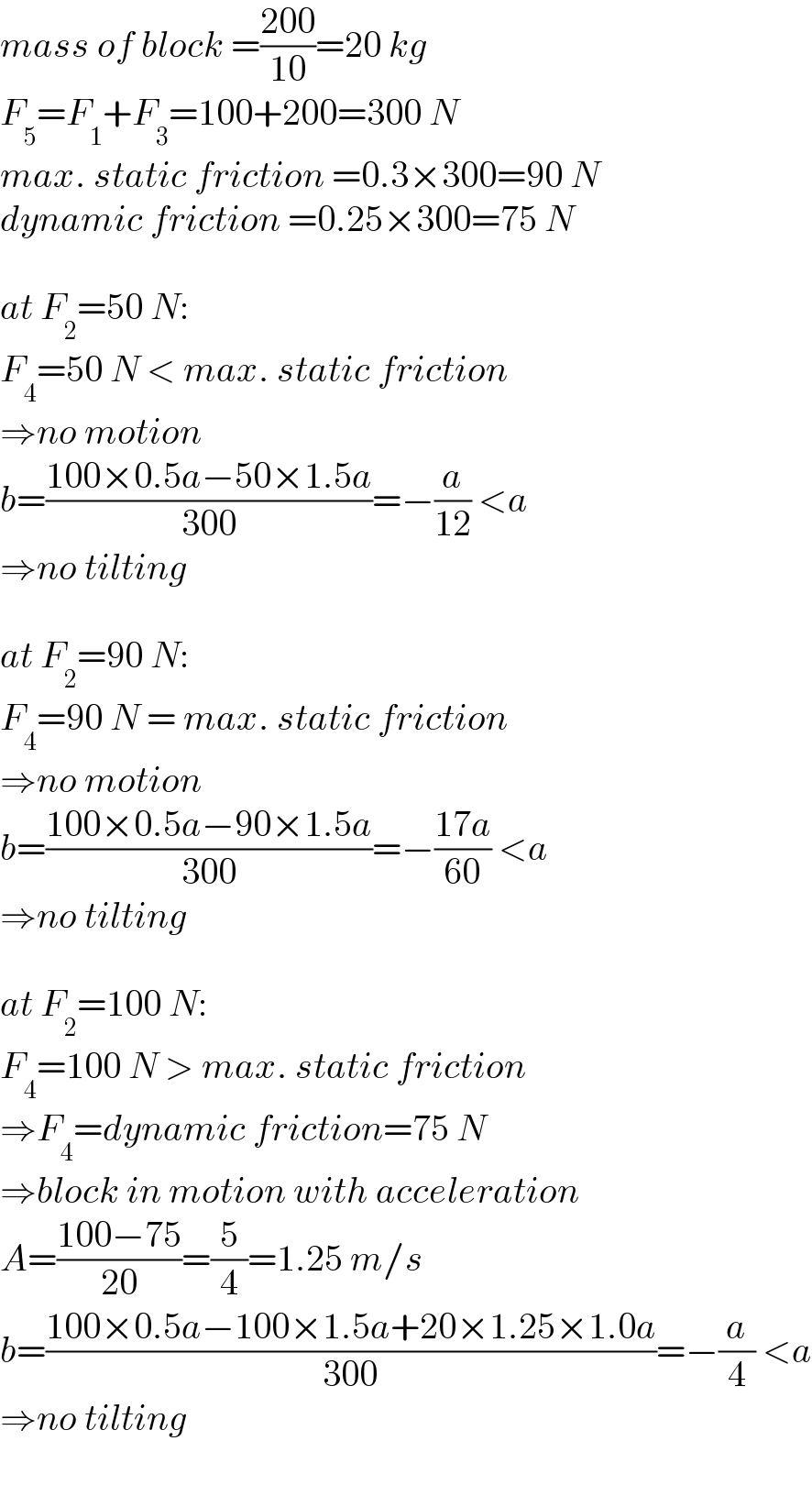
$${mass}\:{of}\:{block}\:=\frac{\mathrm{200}}{\mathrm{10}}=\mathrm{20}\:{kg} \\ $$$${F}_{\mathrm{5}} ={F}_{\mathrm{1}} +{F}_{\mathrm{3}} =\mathrm{100}+\mathrm{200}=\mathrm{300}\:{N} \\ $$$${max}.\:{static}\:{friction}\:=\mathrm{0}.\mathrm{3}×\mathrm{300}=\mathrm{90}\:{N} \\ $$$${dynamic}\:{friction}\:=\mathrm{0}.\mathrm{25}×\mathrm{300}=\mathrm{75}\:{N} \\ $$$$ \\ $$$${at}\:{F}_{\mathrm{2}} =\mathrm{50}\:{N}: \\ $$$${F}_{\mathrm{4}} =\mathrm{50}\:{N}\:<\:{max}.\:{static}\:{friction} \\ $$$$\Rightarrow{no}\:{motion} \\ $$$${b}=\frac{\mathrm{100}×\mathrm{0}.\mathrm{5}{a}−\mathrm{50}×\mathrm{1}.\mathrm{5}{a}}{\mathrm{300}}=−\frac{{a}}{\mathrm{12}}\:<{a} \\ $$$$\Rightarrow{no}\:{tilting} \\ $$$$ \\ $$$${at}\:{F}_{\mathrm{2}} =\mathrm{90}\:{N}: \\ $$$${F}_{\mathrm{4}} =\mathrm{90}\:{N}\:=\:{max}.\:{static}\:{friction} \\ $$$$\Rightarrow{no}\:{motion} \\ $$$${b}=\frac{\mathrm{100}×\mathrm{0}.\mathrm{5}{a}−\mathrm{90}×\mathrm{1}.\mathrm{5}{a}}{\mathrm{300}}=−\frac{\mathrm{17}{a}}{\mathrm{60}}\:<{a} \\ $$$$\Rightarrow{no}\:{tilting} \\ $$$$ \\ $$$${at}\:{F}_{\mathrm{2}} =\mathrm{100}\:{N}: \\ $$$${F}_{\mathrm{4}} =\mathrm{100}\:{N}\:>\:{max}.\:{static}\:{friction} \\ $$$$\Rightarrow{F}_{\mathrm{4}} ={dynamic}\:{friction}=\mathrm{75}\:{N} \\ $$$$\Rightarrow{block}\:{in}\:{motion}\:{with}\:{acceleration} \\ $$$${A}=\frac{\mathrm{100}−\mathrm{75}}{\mathrm{20}}=\frac{\mathrm{5}}{\mathrm{4}}=\mathrm{1}.\mathrm{25}\:{m}/{s} \\ $$$${b}=\frac{\mathrm{100}×\mathrm{0}.\mathrm{5}{a}−\mathrm{100}×\mathrm{1}.\mathrm{5}{a}+\mathrm{20}×\mathrm{1}.\mathrm{25}×\mathrm{1}.\mathrm{0}{a}}{\mathrm{300}}=−\frac{{a}}{\mathrm{4}}\:<{a} \\ $$$$\Rightarrow{no}\:{tilting} \\ $$
