Question Number 136279 by aupo14 last updated on 20/Mar/21
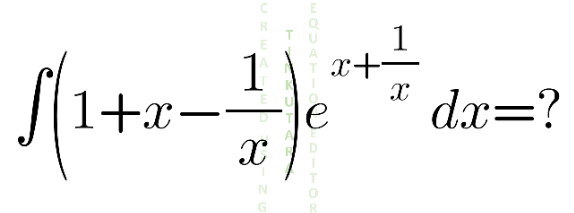
Answered by mindispower last updated on 20/Mar/21
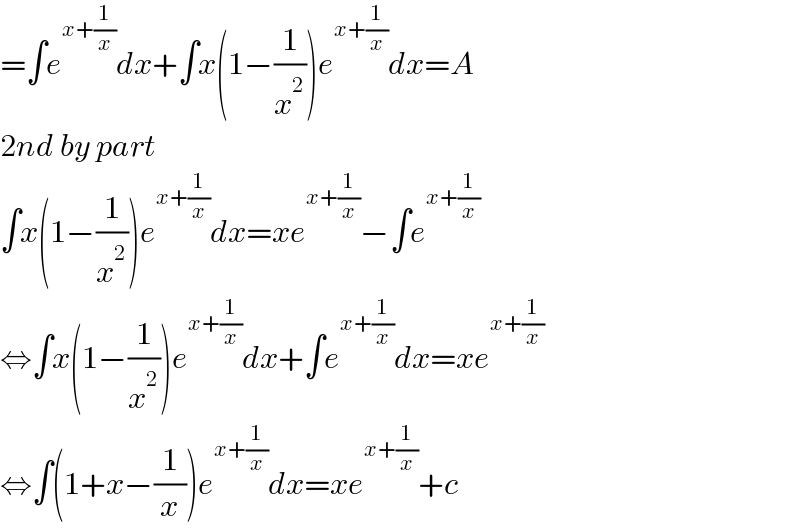
$$=\int{e}^{{x}+\frac{\mathrm{1}}{{x}}} {dx}+\int{x}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right){e}^{{x}+\frac{\mathrm{1}}{{x}}} {dx}={A} \\ $$$$\mathrm{2}{nd}\:{by}\:{part} \\ $$$$\int{x}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right){e}^{{x}+\frac{\mathrm{1}}{{x}}} {dx}={xe}^{{x}+\frac{\mathrm{1}}{{x}}} −\int{e}^{{x}+\frac{\mathrm{1}}{{x}}} \\ $$$$\Leftrightarrow\int{x}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right){e}^{{x}+\frac{\mathrm{1}}{{x}}} {dx}+\int{e}^{{x}+\frac{\mathrm{1}}{{x}}} {dx}={xe}^{{x}+\frac{\mathrm{1}}{{x}}} \\ $$$$\Leftrightarrow\int\left(\mathrm{1}+{x}−\frac{\mathrm{1}}{{x}}\right){e}^{{x}+\frac{\mathrm{1}}{{x}}} {dx}={xe}^{{x}+\frac{\mathrm{1}}{{x}}} +{c} \\ $$
