Question Number 136353 by BHOOPENDRA last updated on 21/Mar/21

Commented by BHOOPENDRA last updated on 21/Mar/21
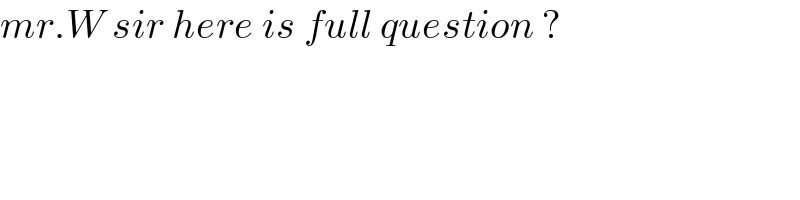
$${mr}.{W}\:{sir}\:{here}\:{is}\:{full}\:{question}\:? \\ $$
Answered by mr W last updated on 21/Mar/21
Commented by mr W last updated on 21/Mar/21
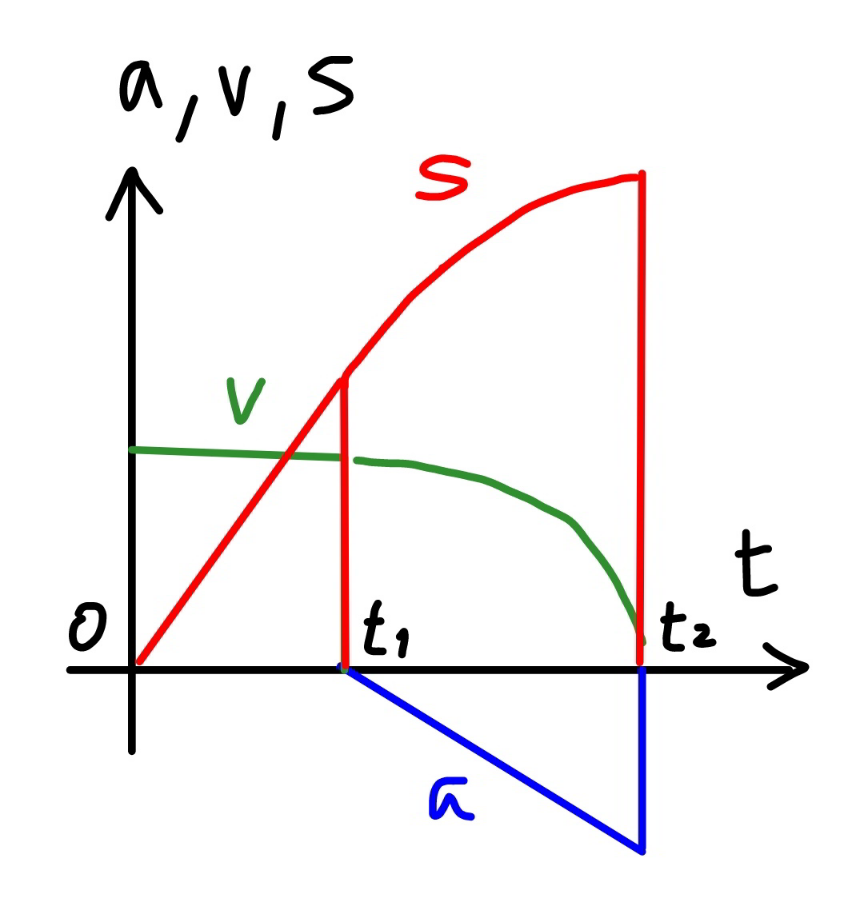
![Part I a(t)= { ((0 for 0≤t<t_1 )),((−c(t−t_1 ) for t_1 ≤t≤t_2 )) :} 0≤t<t_1 : v(t)=v_0 s(t)=v_0 t s(t_1 )=v_0 t_1 t_1 ≤t≤t_2 : v(t)=v_0 +∫_t_1 ^t a(t)dt =v_0 −c∫_t_1 ^t (t−t_1 )dt =v_0 −c[(((t−t_1 )^2 )/2)]_t_1 ^t =v_0 −((c(t−t_1 )^2 )/2) v(t_2 )=v_0 −((c(t_2 −t_1 )^2 )/2)=0 ⇒v_0 =((c(t_2 −t_1 )^2 )/2) s(t)=s(t_1 )+∫_t_1 ^t v(t)dt =v_0 t_1 +∫_t_1 ^t [v_0 −((c(t−t_1 )^2 )/2)]dt =v_0 t_1 +[v_0 t−((c(t−t_1 )^3 )/6)]_t_1 ^t =v_0 t_1 +[v_0 t−((c(t−t_1 )^3 )/6)−v_0 t_1 ] =v_0 t−((c(t−t_1 )^3 )/6)](https://www.tinkutara.com/question/Q136367.png)
$$\boldsymbol{{Part}}\:\boldsymbol{{I}} \\ $$$${a}\left({t}\right)=\begin{cases}{\mathrm{0}\:{for}\:\mathrm{0}\leqslant{t}<{t}_{\mathrm{1}} }\\{−{c}\left({t}−{t}_{\mathrm{1}} \right)\:{for}\:{t}_{\mathrm{1}} \leqslant{t}\leqslant{t}_{\mathrm{2}} }\end{cases} \\ $$$$ \\ $$$$\mathrm{0}\leqslant{t}<{t}_{\mathrm{1}} : \\ $$$${v}\left({t}\right)={v}_{\mathrm{0}} \\ $$$${s}\left({t}\right)={v}_{\mathrm{0}} {t} \\ $$$${s}\left({t}_{\mathrm{1}} \right)={v}_{\mathrm{0}} {t}_{\mathrm{1}} \\ $$$$ \\ $$$${t}_{\mathrm{1}} \leqslant{t}\leqslant{t}_{\mathrm{2}} : \\ $$$${v}\left({t}\right)={v}_{\mathrm{0}} +\int_{{t}_{\mathrm{1}} } ^{{t}} {a}\left({t}\right){dt} \\ $$$$\:\:\:\:\:\:\:\:\:={v}_{\mathrm{0}} −{c}\int_{{t}_{\mathrm{1}} } ^{{t}} \left({t}−{t}_{\mathrm{1}} \right){dt} \\ $$$$\:\:\:\:\:\:\:\:\:={v}_{\mathrm{0}} −{c}\left[\frac{\left({t}−{t}_{\mathrm{1}} \right)^{\mathrm{2}} }{\mathrm{2}}\right]_{{t}_{\mathrm{1}} } ^{{t}} \\ $$$$\:\:\:\:\:\:\:\:\:={v}_{\mathrm{0}} −\frac{{c}\left({t}−{t}_{\mathrm{1}} \right)^{\mathrm{2}} }{\mathrm{2}} \\ $$$${v}\left({t}_{\mathrm{2}} \right)={v}_{\mathrm{0}} −\frac{{c}\left({t}_{\mathrm{2}} −{t}_{\mathrm{1}} \right)^{\mathrm{2}} }{\mathrm{2}}=\mathrm{0} \\ $$$$\Rightarrow{v}_{\mathrm{0}} =\frac{{c}\left({t}_{\mathrm{2}} −{t}_{\mathrm{1}} \right)^{\mathrm{2}} }{\mathrm{2}} \\ $$$${s}\left({t}\right)={s}\left({t}_{\mathrm{1}} \right)+\int_{{t}_{\mathrm{1}} } ^{{t}} {v}\left({t}\right){dt} \\ $$$$\:\:\:\:\:\:\:={v}_{\mathrm{0}} {t}_{\mathrm{1}} +\int_{{t}_{\mathrm{1}} } ^{{t}} \left[{v}_{\mathrm{0}} −\frac{{c}\left({t}−{t}_{\mathrm{1}} \right)^{\mathrm{2}} }{\mathrm{2}}\right]{dt} \\ $$$$\:\:\:\:\:\:\:={v}_{\mathrm{0}} {t}_{\mathrm{1}} +\left[{v}_{\mathrm{0}} {t}−\frac{{c}\left({t}−{t}_{\mathrm{1}} \right)^{\mathrm{3}} }{\mathrm{6}}\right]_{{t}_{\mathrm{1}} } ^{{t}} \\ $$$$\:\:\:\:\:\:\:={v}_{\mathrm{0}} {t}_{\mathrm{1}} +\left[{v}_{\mathrm{0}} {t}−\frac{{c}\left({t}−{t}_{\mathrm{1}} \right)^{\mathrm{3}} }{\mathrm{6}}−{v}_{\mathrm{0}} {t}_{\mathrm{1}} \right] \\ $$$$\:\:\:\:\:\:\:={v}_{\mathrm{0}} {t}−\frac{{c}\left({t}−{t}_{\mathrm{1}} \right)^{\mathrm{3}} }{\mathrm{6}} \\ $$
Commented by mr W last updated on 21/Mar/21
Commented by BHOOPENDRA last updated on 21/Mar/21

$${thanku}\:{sir} \\ $$
Commented by BHOOPENDRA last updated on 21/Mar/21

$${part}\:{b}\:{sir}? \\ $$
Commented by mr W last updated on 21/Mar/21

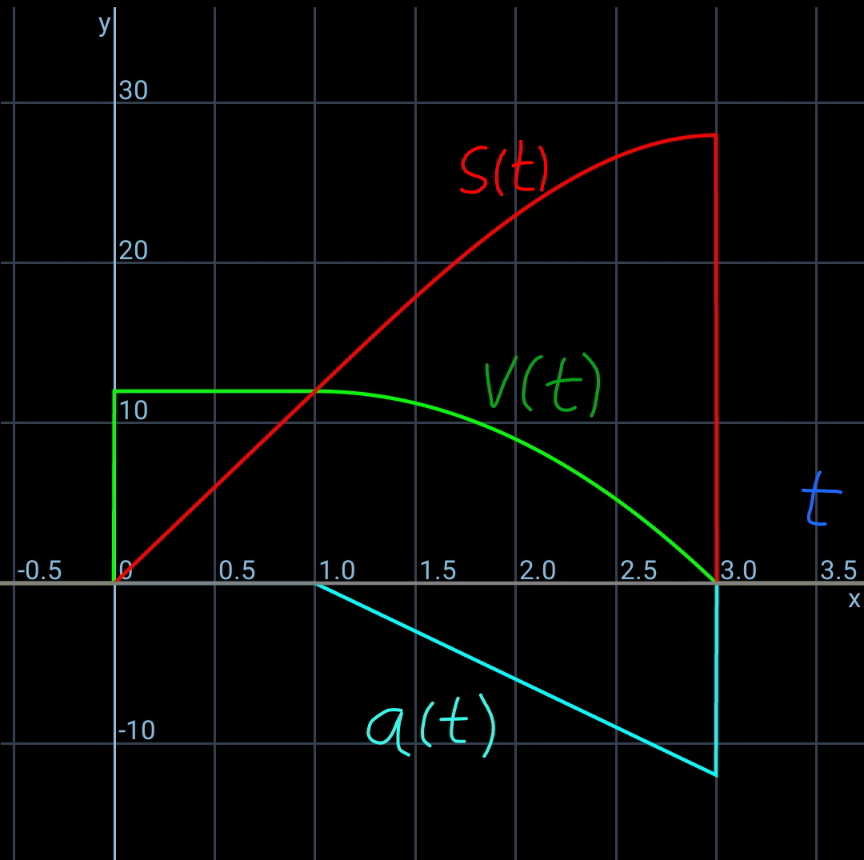
$$\boldsymbol{{Part}}\:\boldsymbol{{II}} \\ $$$${given}\:{c}=\mathrm{6}\:{m}/{s}^{\mathrm{3}} ,\:{t}_{\mathrm{1}} =\mathrm{1}\:{s},\:{v}_{\mathrm{0}} =\mathrm{12}\:{m}/{s}^{\mathrm{2}} \\ $$$${v}_{\mathrm{0}} =\frac{{c}\left({t}_{\mathrm{2}} −{t}_{\mathrm{1}} \right)^{\mathrm{2}} }{\mathrm{2}}=\frac{\mathrm{6}\left({t}_{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}}=\mathrm{12} \\ $$$$\Rightarrow{t}_{\mathrm{2}} =\mathrm{3}\:{s} \\ $$$${s}\left({t}_{\mathrm{2}} \right)={v}_{\mathrm{0}} {t}_{\mathrm{2}} −\frac{{c}\left({t}_{\mathrm{2}} −{t}_{\mathrm{1}} \right)^{\mathrm{3}} }{\mathrm{6}} \\ $$$$\:\:\:\:=\mathrm{12}×\mathrm{3}−\frac{\mathrm{6}\left(\mathrm{3}−\mathrm{1}\right)^{\mathrm{3}} }{\mathrm{6}}=\mathrm{28}\:{m} \\ $$$${velocity}\:{of}\:{biker}: \\ $$$${v}_{{B}} =\frac{\mathrm{17}+\mathrm{28}}{\mathrm{3}}=\mathrm{15}\:{m}/{s} \\ $$
Commented by BHOOPENDRA last updated on 21/Mar/21

$${thanks}\:{sir} \\ $$
