Question Number 136355 by mohammad17 last updated on 21/Mar/21
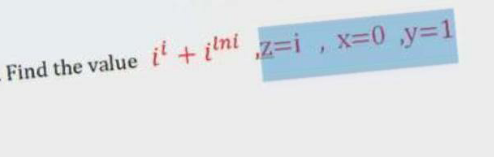
Answered by Dwaipayan Shikari last updated on 21/Mar/21
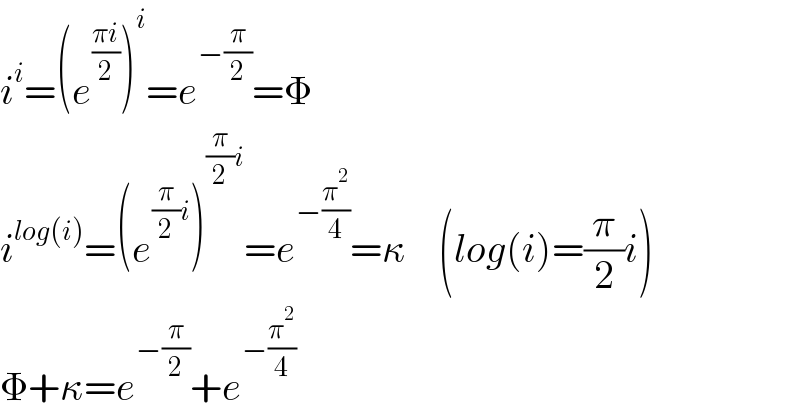
$${i}^{{i}} =\left({e}^{\frac{\pi{i}}{\mathrm{2}}} \right)^{{i}} ={e}^{−\frac{\pi}{\mathrm{2}}} =\Phi \\ $$$${i}^{{log}\left({i}\right)} =\left({e}^{\frac{\pi}{\mathrm{2}}{i}} \right)^{\frac{\pi}{\mathrm{2}}{i}} ={e}^{−\frac{\pi^{\mathrm{2}} }{\mathrm{4}}} =\kappa\:\:\:\:\left({log}\left({i}\right)=\frac{\pi}{\mathrm{2}}{i}\right) \\ $$$$\Phi+\kappa={e}^{−\frac{\pi}{\mathrm{2}}} +{e}^{−\frac{\pi^{\mathrm{2}} }{\mathrm{4}}} \\ $$
Commented by mohammad17 last updated on 21/Mar/21

$${thank}\:{you}\:{sir} \\ $$
