Question Number 136377 by MJS_new last updated on 21/Mar/21
Commented by MJS_new last updated on 21/Mar/21

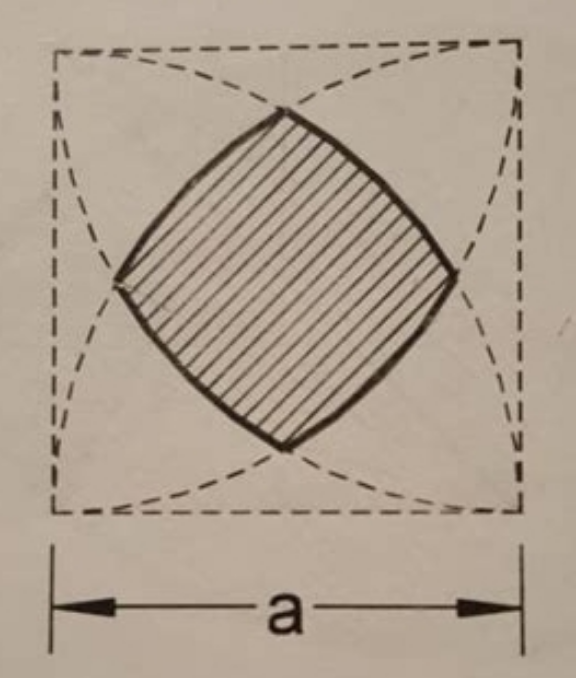
$$\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{the}\:“\mathrm{square}''\:\mathrm{is}\:\left(\frac{\pi}{\mathrm{3}}+\mathrm{1}−\sqrt{\mathrm{3}}\right){a}^{\mathrm{2}} \:\mathrm{but} \\ $$$$\mathrm{how}\:\mathrm{to}\:\mathrm{get}\:\mathrm{this}\:{without}\:\mathrm{integration}? \\ $$$$\mathrm{I}'\mathrm{m}\:\mathrm{afraid}\:\mathrm{I}'\mathrm{m}\:\mathrm{a}\:\mathrm{blockhead}… \\ $$
Answered by mr W last updated on 21/Mar/21
Commented by mr W last updated on 21/Mar/21
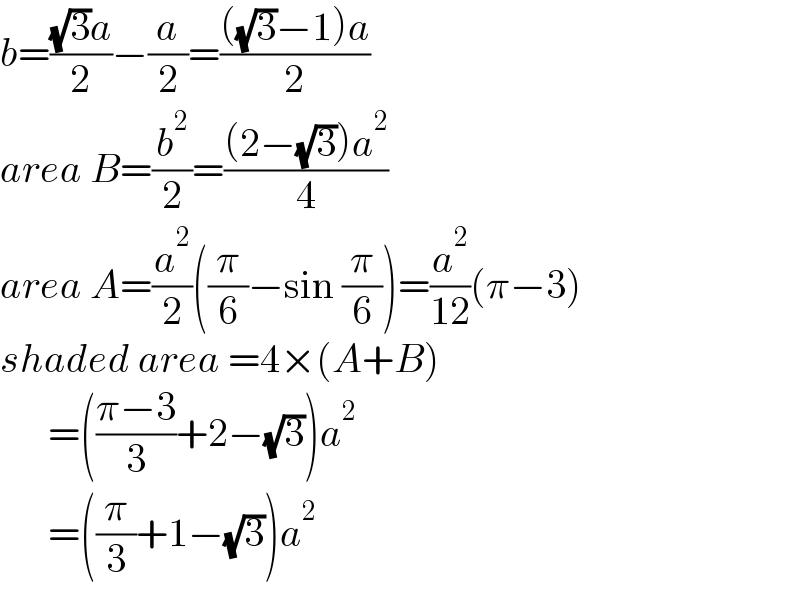
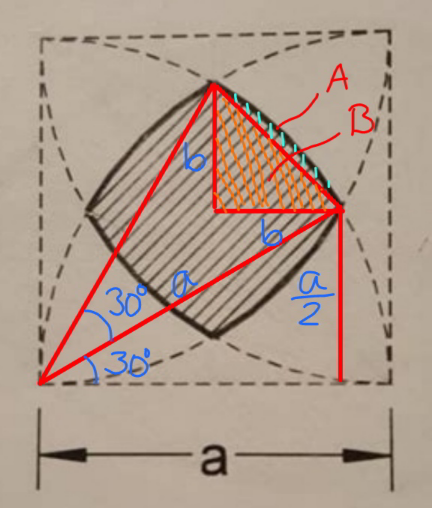
$${b}=\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{2}}−\frac{{a}}{\mathrm{2}}=\frac{\left(\sqrt{\mathrm{3}}−\mathrm{1}\right){a}}{\mathrm{2}} \\ $$$${area}\:{B}=\frac{{b}^{\mathrm{2}} }{\mathrm{2}}=\frac{\left(\mathrm{2}−\sqrt{\mathrm{3}}\right){a}^{\mathrm{2}} }{\mathrm{4}} \\ $$$${area}\:{A}=\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\left(\frac{\pi}{\mathrm{6}}−\mathrm{sin}\:\frac{\pi}{\mathrm{6}}\right)=\frac{{a}^{\mathrm{2}} }{\mathrm{12}}\left(\pi−\mathrm{3}\right) \\ $$$${shaded}\:{area}\:=\mathrm{4}×\left({A}+{B}\right) \\ $$$$\:\:\:\:\:\:=\left(\frac{\pi−\mathrm{3}}{\mathrm{3}}+\mathrm{2}−\sqrt{\mathrm{3}}\right){a}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:=\left(\frac{\pi}{\mathrm{3}}+\mathrm{1}−\sqrt{\mathrm{3}}\right){a}^{\mathrm{2}} \\ $$
Commented by MJS_new last updated on 21/Mar/21
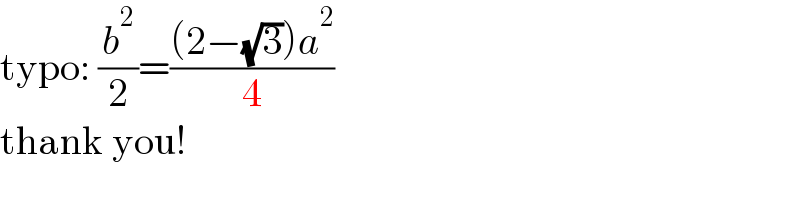
$$\mathrm{typo}:\:\frac{{b}^{\mathrm{2}} }{\mathrm{2}}=\frac{\left(\mathrm{2}−\sqrt{\mathrm{3}}\right){a}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\mathrm{thank}\:\mathrm{you}! \\ $$
Commented by mr W last updated on 21/Mar/21

$${now}\:{fixed}. \\ $$
