Question Number 136415 by ajfour last updated on 21/Mar/21
Commented by ajfour last updated on 21/Mar/21
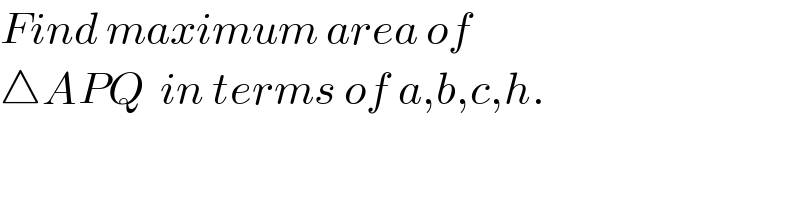
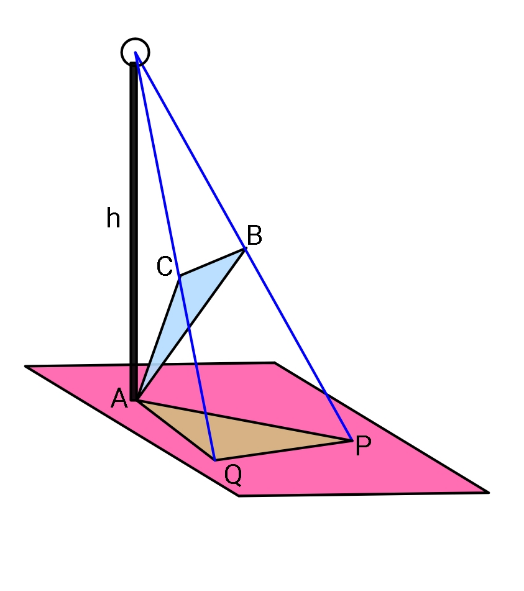
$${Find}\:{maximum}\:{area}\:{of} \\ $$$$\bigtriangleup{APQ}\:\:{in}\:{terms}\:{of}\:{a},{b},{c},{h}. \\ $$
Answered by mr W last updated on 24/Mar/21
Commented by mr W last updated on 27/Mar/21
![classic way z_C =p y_C =0 x_C =(√(b^2 −p^2 )) z_B =q y_B =r x_B ^2 =c^2 −q^2 −r^2 BC^2 =(q−p)^2 +r^2 +(x_B −(√(b^2 −p^2 )))^2 =a^2 c^2 +b^2 −2pq−2x_B (√(b^2 −p^2 ))=a^2 pq+x_B (√(b^2 −p^2 ))=((b^2 +c^2 −a^2 )/2)=k x_B =((k−pq)/( (√(b^2 −p^2 )))) ⇒r^2 =c^2 −q^2 −(((k−pq)^2 )/(b^2 −p^2 )) (x_Q /x_C )=(h/(h−p)) x_Q =((h(√(b^2 −p^2 )))/(h−p)) (y_P /y_B )=(h/(h−q)) y_P =((hr)/(h−q)) shadow area APQ A=((x_Q y_P )/2) =((h^2 r(√(b^2 −p^2 )))/(2(h−p)(h−q))) A=((h^2 (√((b^2 −p^2 )(c^2 −q^2 )−(k−pq)^2 )))/(2(h−p)(h−q))) let A^2 =((h^4 Φ)/4) Φ=(((b^2 −p^2 )(c^2 −q^2 )−(k−pq)^2 )/((h−p)^2 (h−q)^2 )) (∂Φ/∂p)=((−2p(c^2 −q^2 )+2q(k−pq))/((h−p)^2 (h−q)^2 ))+2×(((b^2 −p^2 )(c^2 −q^2 )−(k−pq)^2 )/((h−p)^3 (h−q)^2 ))=0 (hp−b^2 )(c^2 −q^2 )=(hq−k)(k−pq) hc^2 p+b^2 q^2 =k(h+p)q+b^2 c^2 −k^2 ...(i) (∂Φ/∂q)=((−2q(b^2 −p^2 )+2p(k−pq))/((h−p)^2 (h−q)^2 ))+2×(((b^2 −p^2 )(c^2 −q^2 )−(k−pq)^2 )/((h−p)^2 (h−q)^3 ))=0 (hq−c^2 )(b^2 −p^2 )=(hp−k)(k−pq) hb^2 q+c^2 p^2 =k(h+q)p+b^2 c^2 −k^2 ...(ii) (ii)−(i): h(b^2 q−c^2 p)+c^2 p^2 −b^2 q^2 =kh(p−q) c^2 p^2 −h(c^2 +k)p−b^2 q^2 +h(b^2 +k)q=0 (I) (ii)+(i): c^2 p(h+p)+b^2 q(h+q)=k[h(p+q)+2pq]+2b^2 c^2 −2k^2 c^2 p^2 +h(c^2 −k)p+b^2 q^2 +h(b^2 −k)q=2kpq+2b^2 c^2 −2k^2 (II) (I)+(II): c^2 p^2 −hkp+hb^2 q=kpq+b^2 c^2 −k^2 (hb^2 −kp)q=b^2 c^2 −k^2 +hkp−c^2 p^2 ⇒q=((b^2 c^2 −k^2 +hkp−c^2 p^2 )/(hb^2 −kp)) (III) put this into (I) to solve for p. example 1: a=5, b=4, c=7, h=10 Δ_(ABC) =9.7980 ⇒p=2.5897, q=5.2984, r=4.0847 ⇒A_(max) =17.8706 example 2: a=5, b=7, c=7, h=10 Δ_(ABC) =16.3459 ⇒p=q=5.5119, r=4.0753 ⇒A_(max) =43.6497 ==================== A=((h^2 (√((b^2 −p^2 )(c^2 −q^2 )−(k−pq)^2 )))/(2(h−p)(h−q))) with q=((b^2 c^2 −k^2 +hkp−c^2 p^2 )/(hb^2 −kp)) k=((b^2 +c^2 −a^2 )/2)](https://www.tinkutara.com/question/Q136485.png)
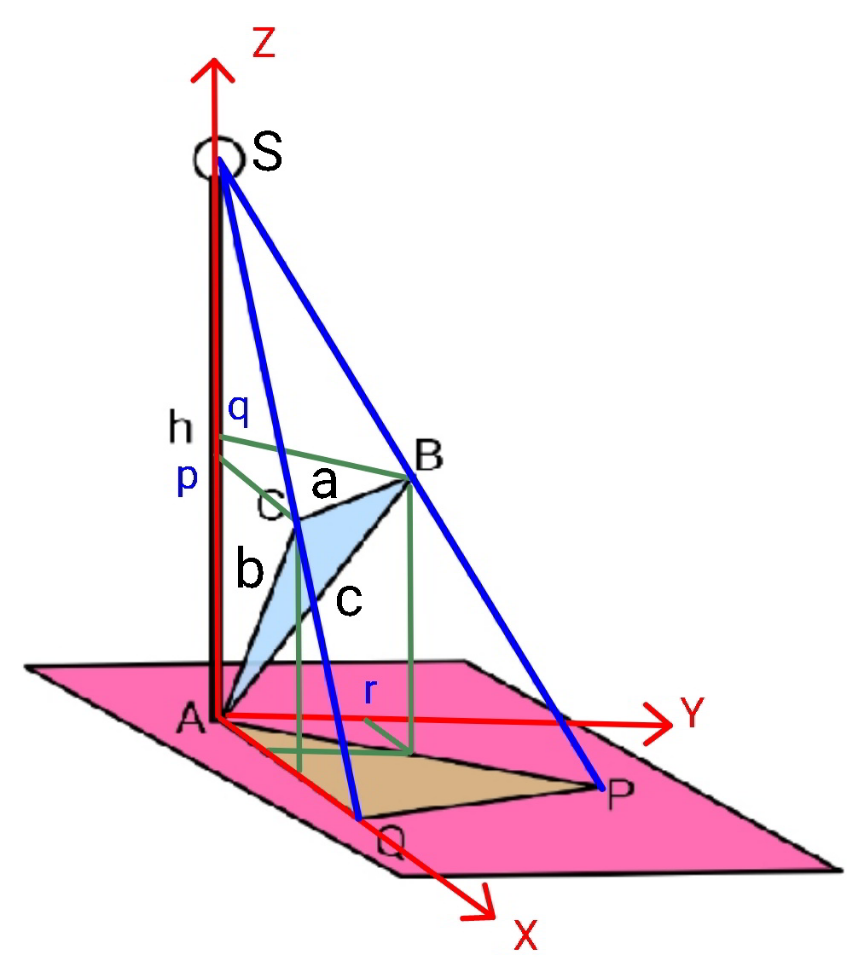
$$\boldsymbol{{classic}}\:\boldsymbol{{way}} \\ $$$${z}_{{C}} ={p} \\ $$$${y}_{{C}} =\mathrm{0} \\ $$$${x}_{{C}} =\sqrt{{b}^{\mathrm{2}} −{p}^{\mathrm{2}} } \\ $$$${z}_{{B}} ={q} \\ $$$${y}_{{B}} ={r} \\ $$$${x}_{{B}} ^{\mathrm{2}} ={c}^{\mathrm{2}} −{q}^{\mathrm{2}} −{r}^{\mathrm{2}} \\ $$$${BC}^{\mathrm{2}} =\left({q}−{p}\right)^{\mathrm{2}} +{r}^{\mathrm{2}} +\left({x}_{{B}} −\sqrt{{b}^{\mathrm{2}} −{p}^{\mathrm{2}} }\right)^{\mathrm{2}} ={a}^{\mathrm{2}} \\ $$$${c}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{pq}−\mathrm{2}{x}_{{B}} \sqrt{{b}^{\mathrm{2}} −{p}^{\mathrm{2}} }={a}^{\mathrm{2}} \\ $$$${pq}+{x}_{{B}} \sqrt{{b}^{\mathrm{2}} −{p}^{\mathrm{2}} }=\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}}={k} \\ $$$${x}_{{B}} =\frac{{k}−{pq}}{\:\sqrt{{b}^{\mathrm{2}} −{p}^{\mathrm{2}} }} \\ $$$$\Rightarrow{r}^{\mathrm{2}} ={c}^{\mathrm{2}} −{q}^{\mathrm{2}} −\frac{\left({k}−{pq}\right)^{\mathrm{2}} }{{b}^{\mathrm{2}} −{p}^{\mathrm{2}} } \\ $$$$\frac{{x}_{{Q}} }{{x}_{{C}} }=\frac{{h}}{{h}−{p}} \\ $$$${x}_{{Q}} =\frac{{h}\sqrt{{b}^{\mathrm{2}} −{p}^{\mathrm{2}} }}{{h}−{p}} \\ $$$$\frac{{y}_{{P}} }{{y}_{{B}} }=\frac{{h}}{{h}−{q}} \\ $$$${y}_{{P}} =\frac{{hr}}{{h}−{q}} \\ $$$${shadow}\:{area}\:{APQ}\:{A}=\frac{{x}_{{Q}} {y}_{{P}} }{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{{h}^{\mathrm{2}} {r}\sqrt{{b}^{\mathrm{2}} −{p}^{\mathrm{2}} }}{\mathrm{2}\left({h}−{p}\right)\left({h}−{q}\right)} \\ $$$${A}=\frac{{h}^{\mathrm{2}} \sqrt{\left({b}^{\mathrm{2}} −{p}^{\mathrm{2}} \right)\left({c}^{\mathrm{2}} −{q}^{\mathrm{2}} \right)−\left({k}−{pq}\right)^{\mathrm{2}} }}{\mathrm{2}\left({h}−{p}\right)\left({h}−{q}\right)} \\ $$$${let}\:{A}^{\mathrm{2}} =\frac{{h}^{\mathrm{4}} \Phi}{\mathrm{4}} \\ $$$$\Phi=\frac{\left({b}^{\mathrm{2}} −{p}^{\mathrm{2}} \right)\left({c}^{\mathrm{2}} −{q}^{\mathrm{2}} \right)−\left({k}−{pq}\right)^{\mathrm{2}} }{\left({h}−{p}\right)^{\mathrm{2}} \left({h}−{q}\right)^{\mathrm{2}} } \\ $$$$\frac{\partial\Phi}{\partial{p}}=\frac{−\mathrm{2}{p}\left({c}^{\mathrm{2}} −{q}^{\mathrm{2}} \right)+\mathrm{2}{q}\left({k}−{pq}\right)}{\left({h}−{p}\right)^{\mathrm{2}} \left({h}−{q}\right)^{\mathrm{2}} }+\mathrm{2}×\frac{\left({b}^{\mathrm{2}} −{p}^{\mathrm{2}} \right)\left({c}^{\mathrm{2}} −{q}^{\mathrm{2}} \right)−\left({k}−{pq}\right)^{\mathrm{2}} }{\left({h}−{p}\right)^{\mathrm{3}} \left({h}−{q}\right)^{\mathrm{2}} }=\mathrm{0} \\ $$$$\left({hp}−{b}^{\mathrm{2}} \right)\left({c}^{\mathrm{2}} −{q}^{\mathrm{2}} \right)=\left({hq}−{k}\right)\left({k}−{pq}\right) \\ $$$${hc}^{\mathrm{2}} {p}+{b}^{\mathrm{2}} {q}^{\mathrm{2}} ={k}\left({h}+{p}\right){q}+{b}^{\mathrm{2}} {c}^{\mathrm{2}} −{k}^{\mathrm{2}} \:\:\:…\left({i}\right) \\ $$$$\frac{\partial\Phi}{\partial{q}}=\frac{−\mathrm{2}{q}\left({b}^{\mathrm{2}} −{p}^{\mathrm{2}} \right)+\mathrm{2}{p}\left({k}−{pq}\right)}{\left({h}−{p}\right)^{\mathrm{2}} \left({h}−{q}\right)^{\mathrm{2}} }+\mathrm{2}×\frac{\left({b}^{\mathrm{2}} −{p}^{\mathrm{2}} \right)\left({c}^{\mathrm{2}} −{q}^{\mathrm{2}} \right)−\left({k}−{pq}\right)^{\mathrm{2}} }{\left({h}−{p}\right)^{\mathrm{2}} \left({h}−{q}\right)^{\mathrm{3}} }=\mathrm{0} \\ $$$$\left({hq}−{c}^{\mathrm{2}} \right)\left({b}^{\mathrm{2}} −{p}^{\mathrm{2}} \right)=\left({hp}−{k}\right)\left({k}−{pq}\right) \\ $$$${hb}^{\mathrm{2}} {q}+{c}^{\mathrm{2}} {p}^{\mathrm{2}} ={k}\left({h}+{q}\right){p}+{b}^{\mathrm{2}} {c}^{\mathrm{2}} −{k}^{\mathrm{2}} \:\:\:…\left({ii}\right) \\ $$$$ \\ $$$$\left({ii}\right)−\left({i}\right): \\ $$$${h}\left({b}^{\mathrm{2}} {q}−{c}^{\mathrm{2}} {p}\right)+{c}^{\mathrm{2}} {p}^{\mathrm{2}} −{b}^{\mathrm{2}} {q}^{\mathrm{2}} ={kh}\left({p}−{q}\right) \\ $$$${c}^{\mathrm{2}} {p}^{\mathrm{2}} −{h}\left({c}^{\mathrm{2}} +{k}\right){p}−{b}^{\mathrm{2}} {q}^{\mathrm{2}} +{h}\left({b}^{\mathrm{2}} +{k}\right){q}=\mathrm{0}\:\:\:\left({I}\right) \\ $$$$\left({ii}\right)+\left({i}\right): \\ $$$${c}^{\mathrm{2}} {p}\left({h}+{p}\right)+{b}^{\mathrm{2}} {q}\left({h}+{q}\right)={k}\left[{h}\left({p}+{q}\right)+\mathrm{2}{pq}\right]+\mathrm{2}{b}^{\mathrm{2}} {c}^{\mathrm{2}} −\mathrm{2}{k}^{\mathrm{2}} \\ $$$${c}^{\mathrm{2}} {p}^{\mathrm{2}} +{h}\left({c}^{\mathrm{2}} −{k}\right){p}+{b}^{\mathrm{2}} {q}^{\mathrm{2}} +{h}\left({b}^{\mathrm{2}} −{k}\right){q}=\mathrm{2}{kpq}+\mathrm{2}{b}^{\mathrm{2}} {c}^{\mathrm{2}} −\mathrm{2}{k}^{\mathrm{2}} \:\:\:\left({II}\right) \\ $$$$ \\ $$$$\left({I}\right)+\left({II}\right): \\ $$$${c}^{\mathrm{2}} {p}^{\mathrm{2}} −{hkp}+{hb}^{\mathrm{2}} {q}={kpq}+{b}^{\mathrm{2}} {c}^{\mathrm{2}} −{k}^{\mathrm{2}} \\ $$$$\left({hb}^{\mathrm{2}} −{kp}\right){q}={b}^{\mathrm{2}} {c}^{\mathrm{2}} −{k}^{\mathrm{2}} +{hkp}−{c}^{\mathrm{2}} {p}^{\mathrm{2}} \\ $$$$\Rightarrow{q}=\frac{{b}^{\mathrm{2}} {c}^{\mathrm{2}} −{k}^{\mathrm{2}} +{hkp}−{c}^{\mathrm{2}} {p}^{\mathrm{2}} }{{hb}^{\mathrm{2}} −{kp}}\:\:\:\left({III}\right) \\ $$$${put}\:{this}\:{into}\:\left({I}\right)\:{to}\:{solve}\:{for}\:{p}. \\ $$$$ \\ $$$$\underline{{example}\:\mathrm{1}}:\:{a}=\mathrm{5},\:{b}=\mathrm{4},\:{c}=\mathrm{7},\:{h}=\mathrm{10} \\ $$$$\Delta_{{ABC}} =\mathrm{9}.\mathrm{7980} \\ $$$$\Rightarrow{p}=\mathrm{2}.\mathrm{5897},\:{q}=\mathrm{5}.\mathrm{2984},\:{r}=\mathrm{4}.\mathrm{0847} \\ $$$$\Rightarrow{A}_{{max}} =\mathrm{17}.\mathrm{8706} \\ $$$$\underline{{example}\:\mathrm{2}}:\:{a}=\mathrm{5},\:{b}=\mathrm{7},\:{c}=\mathrm{7},\:{h}=\mathrm{10} \\ $$$$\Delta_{{ABC}} =\mathrm{16}.\mathrm{3459} \\ $$$$\Rightarrow{p}={q}=\mathrm{5}.\mathrm{5119},\:{r}=\mathrm{4}.\mathrm{0753} \\ $$$$\Rightarrow{A}_{{max}} =\mathrm{43}.\mathrm{6497} \\ $$$$==================== \\ $$$${A}=\frac{{h}^{\mathrm{2}} \sqrt{\left({b}^{\mathrm{2}} −{p}^{\mathrm{2}} \right)\left({c}^{\mathrm{2}} −{q}^{\mathrm{2}} \right)−\left({k}−{pq}\right)^{\mathrm{2}} }}{\mathrm{2}\left({h}−{p}\right)\left({h}−{q}\right)} \\ $$$${with} \\ $$$${q}=\frac{{b}^{\mathrm{2}} {c}^{\mathrm{2}} −{k}^{\mathrm{2}} +{hkp}−{c}^{\mathrm{2}} {p}^{\mathrm{2}} }{{hb}^{\mathrm{2}} −{kp}} \\ $$$${k}=\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}} \\ $$
Commented by ajfour last updated on 22/Mar/21
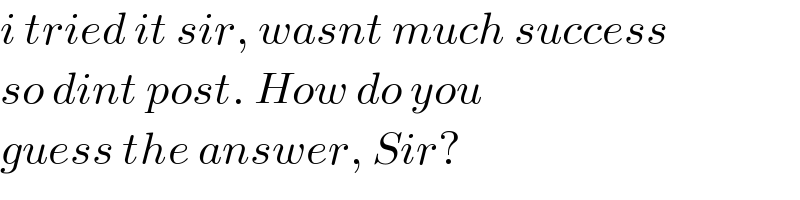
$${i}\:{tried}\:{it}\:{sir},\:{wasnt}\:{much}\:{success} \\ $$$${so}\:{dint}\:{post}.\:{How}\:{do}\:{you} \\ $$$${guess}\:{the}\:{answer},\:{Sir}? \\ $$
Commented by mr W last updated on 28/Mar/21
$${thanks}\:{for}\:{comfirming}\:{sir}! \\ $$
Commented by mr W last updated on 24/Mar/21

$${exact}\:{solution}\:{seems}\:{impossible}\:{to} \\ $$$${me}.\:{i}\:{could}\:{not}\:{find}\:{a}\:{geometric}\:{way} \\ $$$${either}.\:{i}\:{hope}\:{you}'{ll}\:{get}\:{more} \\ $$$${success}\:{through}\:{vector}\:{way}. \\ $$
Commented by ajfour last updated on 24/Mar/21
$${Thanks}\:{for}\:{pursuing}\:{it}\:{till}\:{here} \\ $$$${Sir}.. \\ $$
Commented by ajfour last updated on 24/Mar/21
Commented by ajfour last updated on 24/Mar/21
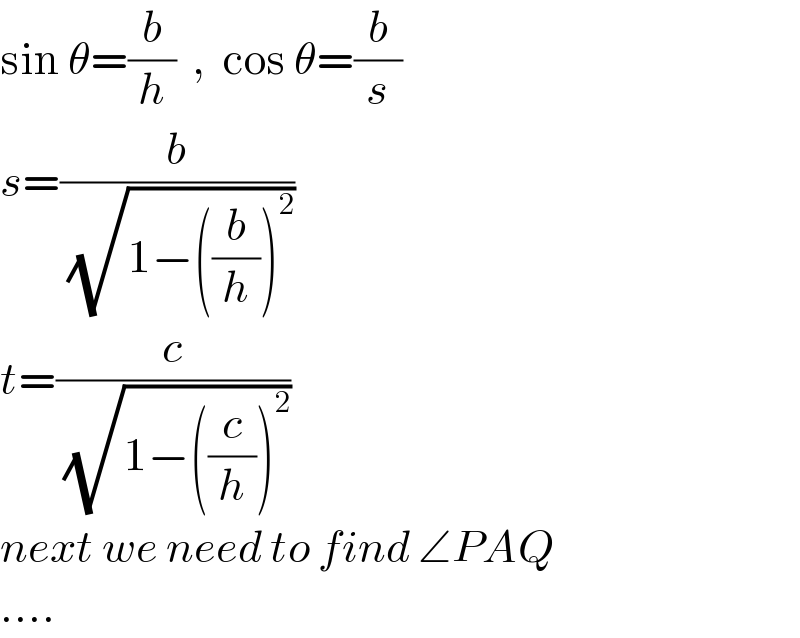
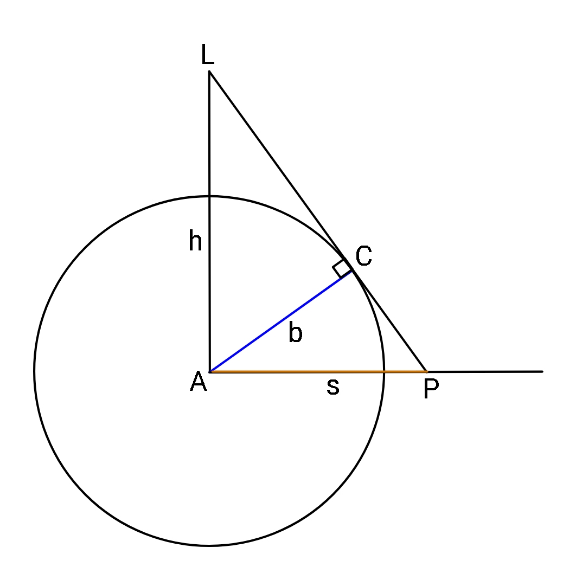
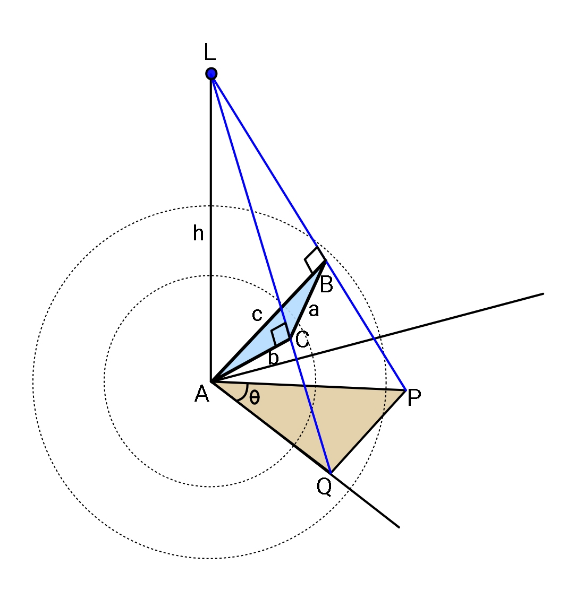
$$\mathrm{sin}\:\theta=\frac{{b}}{{h}}\:\:,\:\:\mathrm{cos}\:\theta=\frac{{b}}{{s}} \\ $$$${s}=\frac{{b}}{\:\sqrt{\mathrm{1}−\left(\frac{{b}}{{h}}\right)^{\mathrm{2}} }} \\ $$$${t}=\frac{{c}}{\:\sqrt{\mathrm{1}−\left(\frac{{c}}{{h}}\right)^{\mathrm{2}} }} \\ $$$${next}\:{we}\:{need}\:{to}\:{find}\:\angle{PAQ} \\ $$$$…. \\ $$
Commented by ajfour last updated on 24/Mar/21
Commented by mr W last updated on 25/Mar/21

$${i}\:{understand}\:{your}\:{thought}.\:{i}\:{did}\:{the} \\ $$$${same},\:{but}\:{it}\:{is}\:{not}\:{correct}.\:{for}\:{area}\:{of} \\ $$$${shadow}\:{it}\:{is}\:{not}\:{obviours}\:{what}\:{makes} \\ $$$${its}\:{area}\:{maximum}.\:{let}'{s}\:{look}\:{the} \\ $$$${symmetrical}\:{case}\:{that}\:{AB}={AC}. \\ $$$${we}\:{may}\:{think}\:{the}\:{area}\:{of}\:{the}\:{shadow} \\ $$$${is}\:{maximum},\:{when}\:\Delta{ABC}\:{stands} \\ $$$${perpendicularly}\:{to}\:{the}\:{line}\:{SR},\:{since} \\ $$$${the}\:{length}\:{of}\:{AR},\:{as}\:{well}\:{as}\:{AP}\:{and} \\ $$$${AQ}\:{are}\:{maximum}.\:{but}\:{this}\:{is}\:{not} \\ $$$${correct},\:{since}\:{the}\:{maximal}\:{length} \\ $$$${of}\:{AP}\:{and}\:{AQ}\:{doesn}'{t}\:{lead}\:{to}\:{the} \\ $$$${maximum}\:{area}\:{of}\:{APQ}. \\ $$
Commented by mr W last updated on 24/Mar/21
Commented by mr W last updated on 24/Mar/21
Commented by mr W last updated on 25/Mar/21
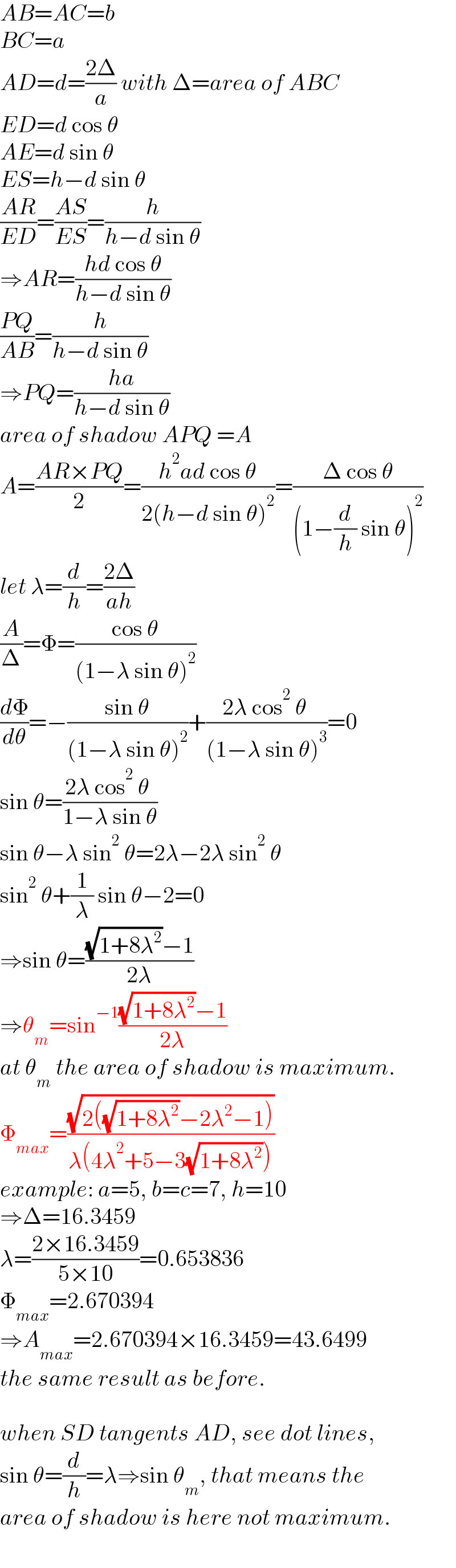
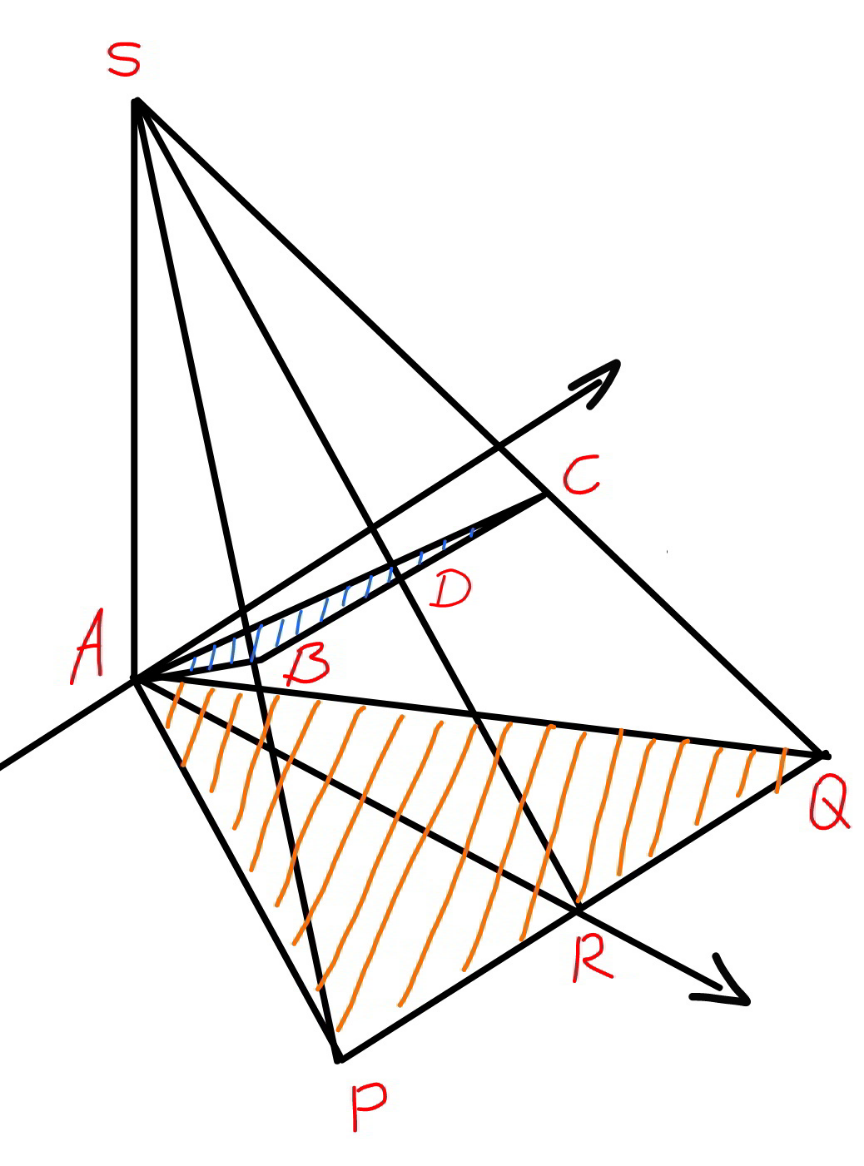
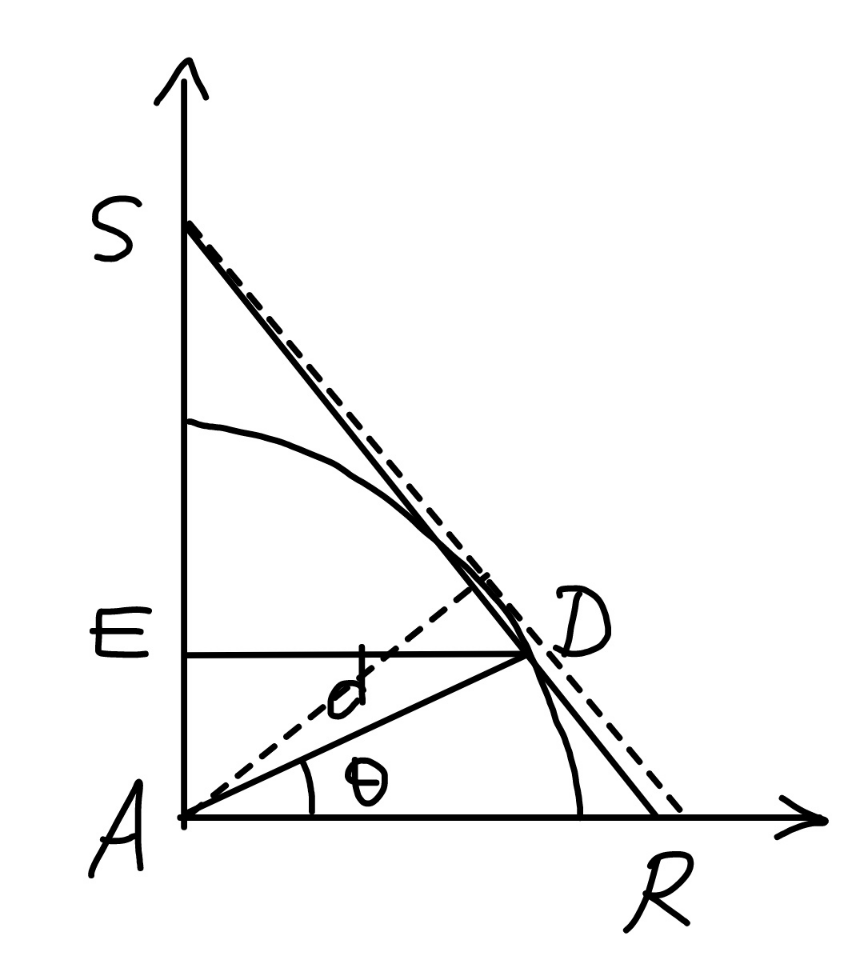
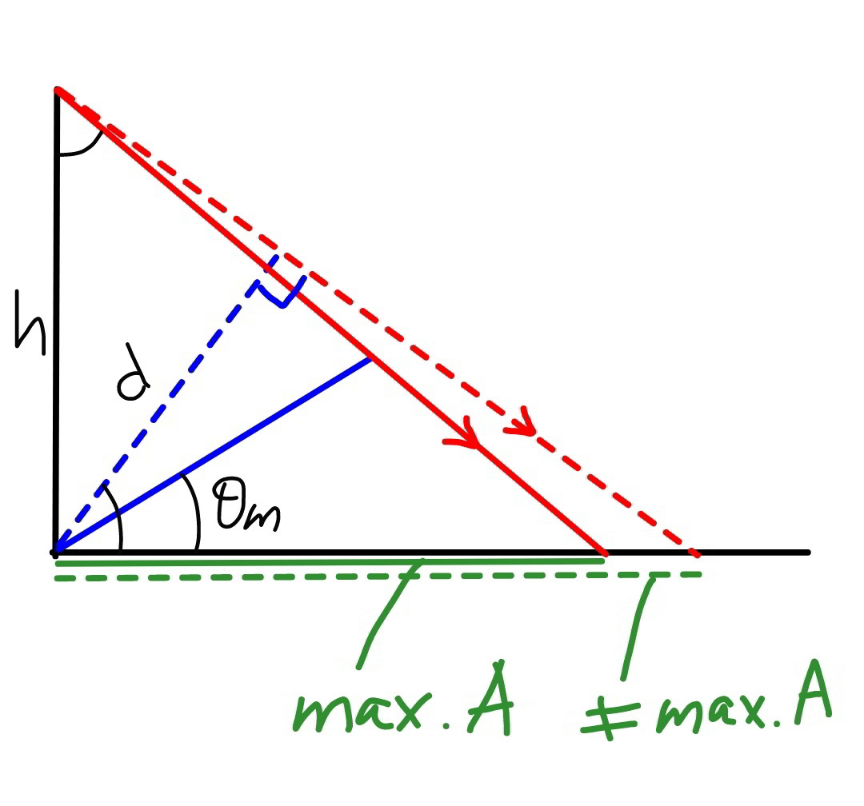
$${AB}={AC}={b} \\ $$$${BC}={a} \\ $$$${AD}={d}=\frac{\mathrm{2}\Delta}{{a}}\:{with}\:\Delta={area}\:{of}\:{ABC} \\ $$$${ED}={d}\:\mathrm{cos}\:\theta \\ $$$${AE}={d}\:\mathrm{sin}\:\theta \\ $$$${ES}={h}−{d}\:\mathrm{sin}\:\theta \\ $$$$\frac{{AR}}{{ED}}=\frac{{AS}}{{ES}}=\frac{{h}}{{h}−{d}\:\mathrm{sin}\:\theta} \\ $$$$\Rightarrow{AR}=\frac{{hd}\:\mathrm{cos}\:\theta}{{h}−{d}\:\mathrm{sin}\:\theta} \\ $$$$\frac{{PQ}}{{AB}}=\frac{{h}}{{h}−{d}\:\mathrm{sin}\:\theta} \\ $$$$\Rightarrow{PQ}=\frac{{ha}}{{h}−{d}\:\mathrm{sin}\:\theta} \\ $$$${area}\:{of}\:{shadow}\:{APQ}\:={A} \\ $$$${A}=\frac{{AR}×{PQ}}{\mathrm{2}}=\frac{{h}^{\mathrm{2}} {ad}\:\mathrm{cos}\:\theta}{\mathrm{2}\left({h}−{d}\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} }=\frac{\Delta\:\mathrm{cos}\:\theta}{\left(\mathrm{1}−\frac{{d}}{{h}}\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} } \\ $$$${let}\:\lambda=\frac{{d}}{{h}}=\frac{\mathrm{2}\Delta}{{ah}} \\ $$$$\frac{{A}}{\Delta}=\Phi=\frac{\mathrm{cos}\:\theta}{\left(\mathrm{1}−\lambda\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} } \\ $$$$\frac{{d}\Phi}{{d}\theta}=−\frac{\mathrm{sin}\:\theta}{\left(\mathrm{1}−\lambda\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} }+\frac{\mathrm{2}\lambda\:\mathrm{cos}^{\mathrm{2}} \:\theta\:}{\left(\mathrm{1}−\lambda\:\mathrm{sin}\:\theta\right)^{\mathrm{3}} }=\mathrm{0} \\ $$$$\mathrm{sin}\:\theta=\frac{\mathrm{2}\lambda\:\mathrm{cos}^{\mathrm{2}} \:\theta\:}{\mathrm{1}−\lambda\:\mathrm{sin}\:\theta} \\ $$$$\mathrm{sin}\:\theta−\lambda\:\mathrm{sin}^{\mathrm{2}} \:\theta=\mathrm{2}\lambda−\mathrm{2}\lambda\:\mathrm{sin}^{\mathrm{2}} \:\theta \\ $$$$\mathrm{sin}^{\mathrm{2}} \:\theta+\frac{\mathrm{1}}{\lambda}\:\mathrm{sin}\:\theta−\mathrm{2}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{sin}\:\theta=\frac{\sqrt{\mathrm{1}+\mathrm{8}\lambda^{\mathrm{2}} }−\mathrm{1}}{\mathrm{2}\lambda} \\ $$$$\Rightarrow\theta_{{m}} =\mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{\mathrm{1}+\mathrm{8}\lambda^{\mathrm{2}} }−\mathrm{1}}{\mathrm{2}\lambda} \\ $$$${at}\:\theta_{{m}} \:{the}\:{area}\:{of}\:{shadow}\:{is}\:{maximum}. \\ $$$$\Phi_{{max}} =\frac{\sqrt{\mathrm{2}\left(\sqrt{\mathrm{1}+\mathrm{8}\lambda^{\mathrm{2}} }−\mathrm{2}\lambda^{\mathrm{2}} −\mathrm{1}\right)}}{\lambda\left(\mathrm{4}\lambda^{\mathrm{2}} +\mathrm{5}−\mathrm{3}\sqrt{\mathrm{1}+\mathrm{8}\lambda^{\mathrm{2}} }\right)} \\ $$$${example}:\:{a}=\mathrm{5},\:{b}={c}=\mathrm{7},\:{h}=\mathrm{10} \\ $$$$\Rightarrow\Delta=\mathrm{16}.\mathrm{3459} \\ $$$$\lambda=\frac{\mathrm{2}×\mathrm{16}.\mathrm{3459}}{\mathrm{5}×\mathrm{10}}=\mathrm{0}.\mathrm{653836} \\ $$$$\Phi_{{max}} =\mathrm{2}.\mathrm{670394} \\ $$$$\Rightarrow{A}_{{max}} =\mathrm{2}.\mathrm{670394}×\mathrm{16}.\mathrm{3459}=\mathrm{43}.\mathrm{6499} \\ $$$${the}\:{same}\:{result}\:{as}\:{before}. \\ $$$$ \\ $$$${when}\:{SD}\:{tangents}\:{AD},\:{see}\:{dot}\:{lines}, \\ $$$$\mathrm{sin}\:\theta=\frac{{d}}{{h}}=\lambda\Rightarrow\mathrm{sin}\:\theta_{{m}} ,\:{that}\:{means}\:{the} \\ $$$${area}\:{of}\:{shadow}\:{is}\:{here}\:{not}\:{maximum}. \\ $$
Commented by mr W last updated on 25/Mar/21

$${if}\:\mathrm{sin}\:\theta_{{m}} =\lambda=\frac{{d}}{{h}}=\frac{\mathrm{2}\Delta}{{ah}} \\ $$$${A}_{{max}} =\Delta×\frac{\mathrm{cos}\:\theta}{\left(\mathrm{1}−\lambda\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} }=\Delta×\frac{\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}{\left(\mathrm{1}−\lambda^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\frac{\Delta}{\left(\mathrm{1}−\lambda^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} }=\frac{\Delta}{\left(\mathrm{1}−\frac{\mathrm{4}\Delta^{\mathrm{2}} }{{a}^{\mathrm{2}} {h}^{\mathrm{2}} }\right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$${this}\:{is}\:{the}\:{formula}\:{which}\:{i}\:{gave} \\ $$$${at}\:{first}.\:{but}\:{now}\:{we}\:{know}\:{it}\:{is}\:{not} \\ $$$${correct}. \\ $$
Commented by mr W last updated on 25/Mar/21
Commented by mr W last updated on 26/Mar/21

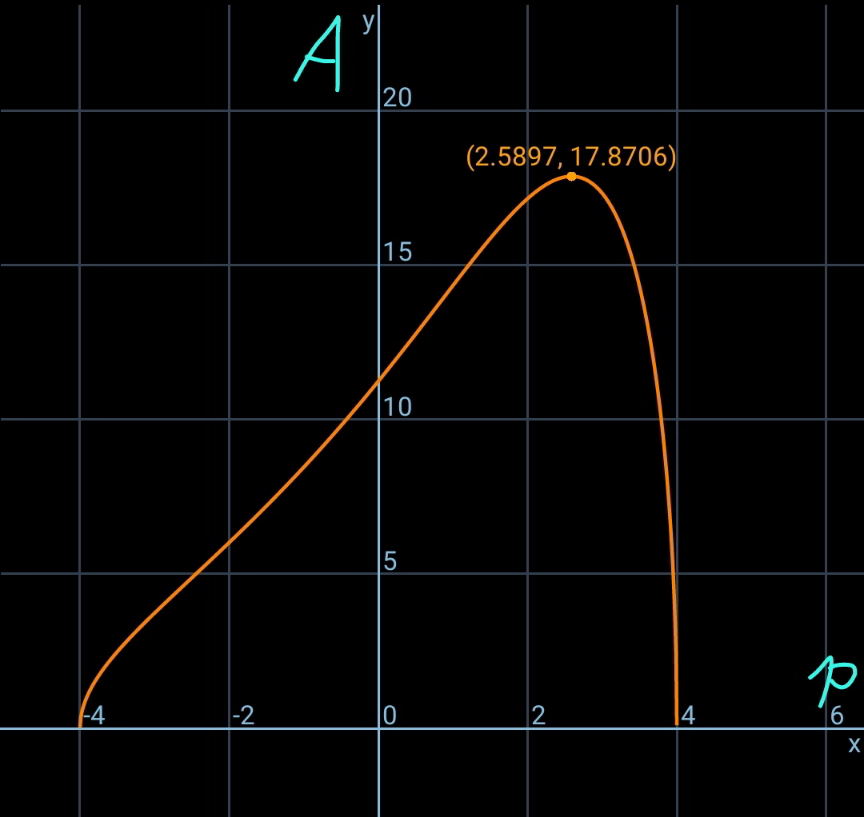
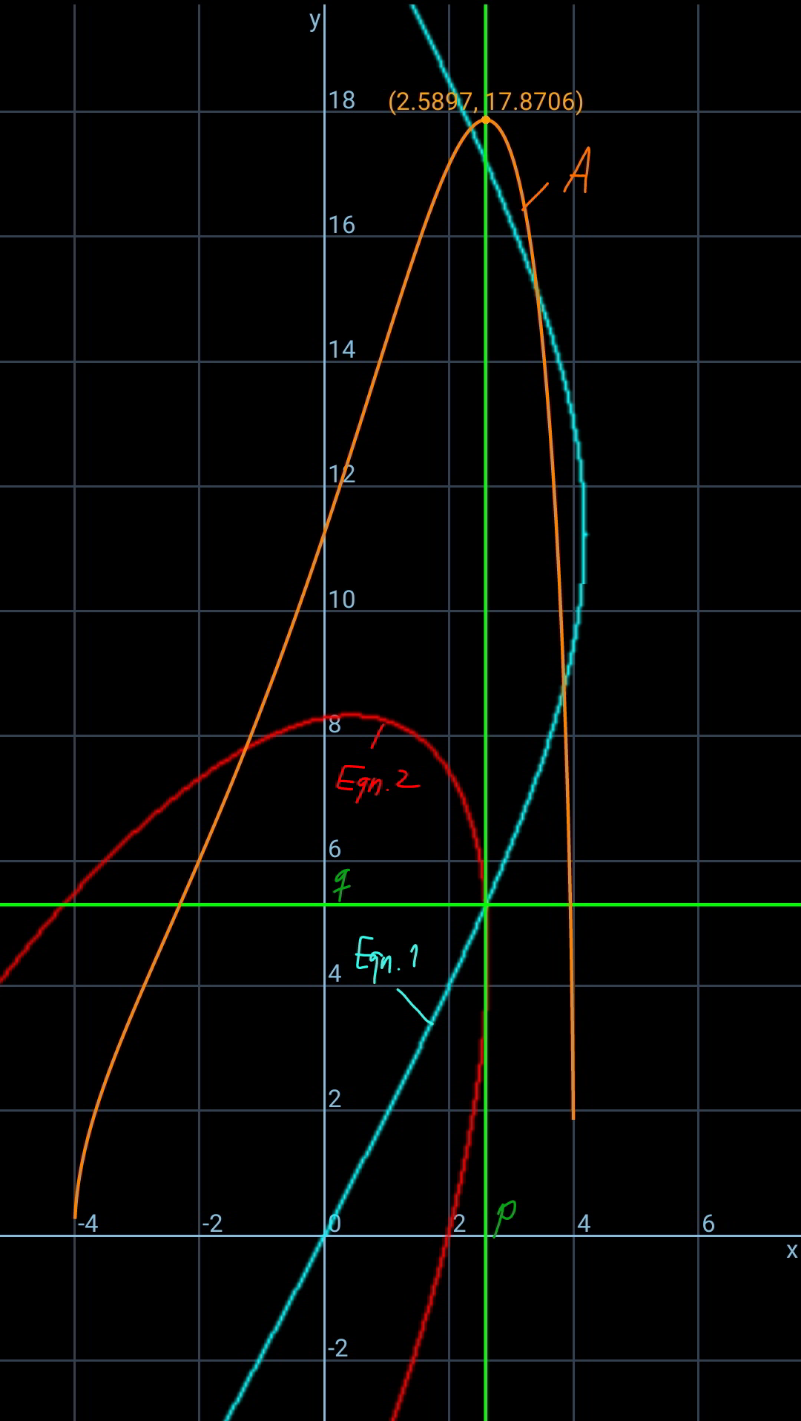
$$\underline{\boldsymbol{{Summary}}} \\ $$$${we}\:{can}\:{express}\:{the}\:{area}\:{of}\:{shadow}\:{as} \\ $$$${a}\:{function}\:{of}\:{a}\:{single}\:{variable}\:{p}: \\ $$$${A}=\frac{{h}^{\mathrm{2}} \sqrt{\left({b}^{\mathrm{2}} −{p}^{\mathrm{2}} \right)\left({c}^{\mathrm{2}} −{q}^{\mathrm{2}} \right)−\left({k}−{pq}\right)^{\mathrm{2}} }}{\mathrm{2}\left({h}−{p}\right)\left({h}−{q}\right)} \\ $$$${with} \\ $$$${q}=\frac{{b}^{\mathrm{2}} {c}^{\mathrm{2}} −{k}^{\mathrm{2}} +{hkp}−{c}^{\mathrm{2}} {p}^{\mathrm{2}} }{{hb}^{\mathrm{2}} −{kp}} \\ $$$${k}=\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${the}\:{maximum}\:{area}\:{of}\:{the}\:{shadow} \\ $$$${can}\:{be}\:{determined}\:{approximately}. \\ $$
Commented by mr W last updated on 26/Mar/21
Commented by mr W last updated on 26/Mar/21
Commented by ajfour last updated on 28/Mar/21
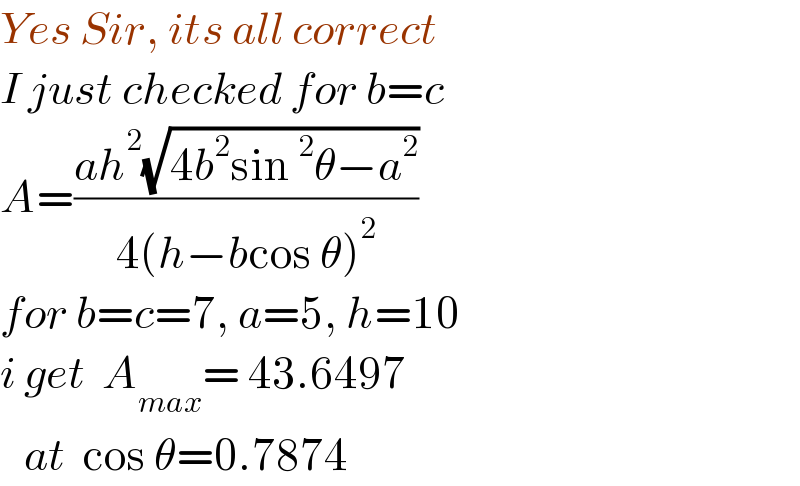
$${Yes}\:{Sir},\:{its}\:{all}\:{correct} \\ $$$${I}\:{just}\:{checked}\:{for}\:{b}={c} \\ $$$${A}=\frac{{ah}^{\mathrm{2}} \sqrt{\mathrm{4}{b}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta−{a}^{\mathrm{2}} }}{\mathrm{4}\left({h}−{b}\mathrm{cos}\:\theta\right)^{\mathrm{2}} } \\ $$$${for}\:{b}={c}=\mathrm{7},\:{a}=\mathrm{5},\:{h}=\mathrm{10}\:\: \\ $$$${i}\:{get}\:\:{A}_{{max}} =\:\mathrm{43}.\mathrm{6497} \\ $$$$\:\:\:{at}\:\:\mathrm{cos}\:\theta=\mathrm{0}.\mathrm{7874} \\ $$
Answered by mr W last updated on 25/Mar/21
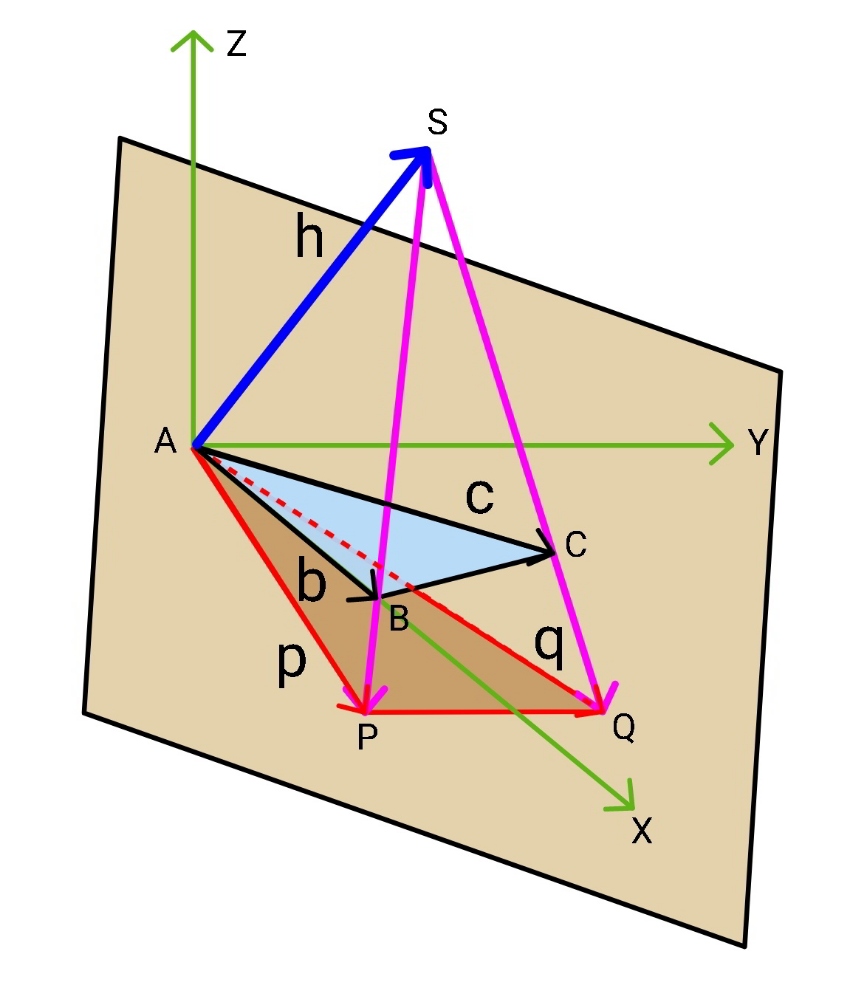
Commented by mr W last updated on 25/Mar/21
![vector way Δ=area of ABC SB=b−h SP=ξ(b−h) AP=h+SP=h+ξ(b−h)=(1−ξ)h+ξb AP∙h=0 (1−ξ)h^2 +ξb∙h=0 ξ=(1/(1−((b∙h)/h^2 ))) p=AP=(1/(1−((b∙h)/h^2 )))(((b∙h)/h^2 )h+b) similarly q=AQ=(1/(1−((c∙h)/h^2 )))(((c∙h)/h^2 )h+c) area of shadow A=(1/2)∣p×q∣ b=(b,0,0) c=(c cos ∠A, c sin ∠A,0) h=(αh,βh,γh) with γ=(√(1−α^2 −β^2 )) b∙h=αhb c∙h=αhc cos ∠A+βhc sin ∠A ⇒p=((bh)/(h−αb))(1+α^2 , αβ, αγ) ⇒q=((ch)/(h−c(α cos ∠A+β sin ∠A)))((1+α^2 ) cos ∠A+αβ sin ∠A, (1+β^2 ) sin ∠A+αβ cos ∠A, (α cos ∠A+β sin ∠A)γ) u=αβ×(α cos ∠A+β sin ∠A)γ−αγ×[(1+β^2 ) sin ∠A+αβ cos ∠A] u=−αγ sin ∠A v=(1+α^2 )×(α cos ∠A+β sin ∠A)γ−αγ×[(1+α^2 ) cos ∠A+αβ sin ∠A] v=−βγ sin ∠A w=(1+α^2 )×[(1+β^2 ) sin ∠A+αβ cos ∠A]−αβ×[(1+α^2 ) cos ∠A+αβ sin A] w=(1+α^2 +β^2 ) sin ∠A (1/2)∣p×q∣=(1/2)×((bh)/(h−αb))×((ch)/(h−c(α cos ∠A+β sin ∠A)))×(√(u^2 +v^2 +z^2 )) ∣p×q∣=((bch^2 sin ∠A(√((α^2 +β^2 )γ^2 +(1+α^2 +β^2 )^2 )))/(2(h−αb)[h−c(α cos ∠A+β sin ∠A)])) ∣p×q∣=((h^2 Δ(√((1−γ^2 )γ^2 +(2−γ^2 )^2 )))/((h−αb)[h−c(α cos ∠A+β sin ∠A)])) ∣p×q∣=((Δ(√(1+3α^2 +3β^2 )))/((1−(b/h)α)[1−(c/h)(α cos ∠A+β sin ∠A)])) let (b/h)=l, ((c cos ∠A)/h)=m, ((c sin ∠A)/h)=n area of shadow A=((Δ(√(1+3α^2 +3β^2 )))/((1−lα)(1−mα−nβ))) =(√Φ)Δ Φ=((1+3α^2 +3β^2 )/((1−lα)^2 (1−mα−nβ)^2 )) .....](https://www.tinkutara.com/question/Q136709.png)
$$\boldsymbol{{vector}}\:\boldsymbol{{way}} \\ $$$$ \\ $$$$\Delta={area}\:{of}\:{ABC} \\ $$$$ \\ $$$$\boldsymbol{{SB}}=\boldsymbol{{b}}−\boldsymbol{{h}} \\ $$$$\boldsymbol{{SP}}=\xi\left(\boldsymbol{{b}}−\boldsymbol{{h}}\right) \\ $$$$\boldsymbol{{AP}}=\boldsymbol{{h}}+\boldsymbol{{SP}}=\boldsymbol{{h}}+\xi\left(\boldsymbol{{b}}−\boldsymbol{{h}}\right)=\left(\mathrm{1}−\xi\right)\boldsymbol{{h}}+\xi\boldsymbol{{b}} \\ $$$$\boldsymbol{{AP}}\centerdot\boldsymbol{{h}}=\mathrm{0} \\ $$$$\left(\mathrm{1}−\xi\right){h}^{\mathrm{2}} +\xi\boldsymbol{{b}}\centerdot\boldsymbol{{h}}=\mathrm{0} \\ $$$$\xi=\frac{\mathrm{1}}{\mathrm{1}−\frac{\boldsymbol{{b}}\centerdot\boldsymbol{{h}}}{{h}^{\mathrm{2}} }} \\ $$$$\boldsymbol{{p}}=\boldsymbol{{AP}}=\frac{\mathrm{1}}{\mathrm{1}−\frac{\boldsymbol{{b}}\centerdot\boldsymbol{{h}}}{{h}^{\mathrm{2}} }}\left(\frac{\boldsymbol{{b}}\centerdot\boldsymbol{{h}}}{{h}^{\mathrm{2}} }\boldsymbol{{h}}+\boldsymbol{{b}}\right) \\ $$$${similarly} \\ $$$$\boldsymbol{{q}}=\boldsymbol{{AQ}}=\frac{\mathrm{1}}{\mathrm{1}−\frac{\boldsymbol{{c}}\centerdot\boldsymbol{{h}}}{{h}^{\mathrm{2}} }}\left(\frac{\boldsymbol{{c}}\centerdot\boldsymbol{{h}}}{{h}^{\mathrm{2}} }\boldsymbol{{h}}+\boldsymbol{{c}}\right) \\ $$$${area}\:{of}\:{shadow}\:{A}=\frac{\mathrm{1}}{\mathrm{2}}\mid\boldsymbol{{p}}×\boldsymbol{{q}}\mid \\ $$$$\boldsymbol{{b}}=\left({b},\mathrm{0},\mathrm{0}\right) \\ $$$$\boldsymbol{{c}}=\left({c}\:\mathrm{cos}\:\angle{A},\:{c}\:\mathrm{sin}\:\angle{A},\mathrm{0}\right) \\ $$$$\boldsymbol{{h}}=\left(\alpha{h},\beta{h},\gamma{h}\right)\:{with}\:\gamma=\sqrt{\mathrm{1}−\alpha^{\mathrm{2}} −\beta^{\mathrm{2}} } \\ $$$$\boldsymbol{{b}}\centerdot\boldsymbol{{h}}=\alpha{hb} \\ $$$$\boldsymbol{{c}}\centerdot\boldsymbol{{h}}=\alpha{hc}\:\mathrm{cos}\:\angle{A}+\beta{hc}\:\mathrm{sin}\:\angle{A} \\ $$$$\Rightarrow\boldsymbol{{p}}=\frac{{bh}}{{h}−\alpha{b}}\left(\mathrm{1}+\alpha^{\mathrm{2}} ,\:\alpha\beta,\:\alpha\gamma\right) \\ $$$$\Rightarrow\boldsymbol{{q}}=\frac{{ch}}{{h}−{c}\left(\alpha\:\mathrm{cos}\:\angle{A}+\beta\:\mathrm{sin}\:\angle{A}\right)}\left(\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)\:\mathrm{cos}\:\angle{A}+\alpha\beta\:\mathrm{sin}\:\angle{A},\:\left(\mathrm{1}+\beta^{\mathrm{2}} \right)\:\mathrm{sin}\:\angle{A}+\alpha\beta\:\mathrm{cos}\:\angle{A},\:\left(\alpha\:\mathrm{cos}\:\angle{A}+\beta\:\mathrm{sin}\:\angle{A}\right)\gamma\right) \\ $$$${u}=\alpha\beta×\left(\alpha\:\mathrm{cos}\:\angle{A}+\beta\:\mathrm{sin}\:\angle{A}\right)\gamma−\alpha\gamma×\left[\left(\mathrm{1}+\beta^{\mathrm{2}} \right)\:\mathrm{sin}\:\angle{A}+\alpha\beta\:\mathrm{cos}\:\angle{A}\right] \\ $$$${u}=−\alpha\gamma\:\mathrm{sin}\:\angle{A} \\ $$$${v}=\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)×\left(\alpha\:\mathrm{cos}\:\angle{A}+\beta\:\mathrm{sin}\:\angle{A}\right)\gamma−\alpha\gamma×\left[\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)\:\mathrm{cos}\:\angle{A}+\alpha\beta\:\mathrm{sin}\:\angle{A}\right] \\ $$$${v}=−\beta\gamma\:\mathrm{sin}\:\angle{A} \\ $$$${w}=\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)×\left[\left(\mathrm{1}+\beta^{\mathrm{2}} \right)\:\mathrm{sin}\:\angle{A}+\alpha\beta\:\mathrm{cos}\:\angle{A}\right]−\alpha\beta×\left[\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)\:\mathrm{cos}\:\angle{A}+\alpha\beta\:\mathrm{sin}\:{A}\right] \\ $$$${w}=\left(\mathrm{1}+\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} \right)\:\mathrm{sin}\:\angle{A} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\mid\boldsymbol{{p}}×\boldsymbol{{q}}\mid=\frac{\mathrm{1}}{\mathrm{2}}×\frac{{bh}}{{h}−\alpha{b}}×\frac{{ch}}{{h}−{c}\left(\alpha\:\mathrm{cos}\:\angle{A}+\beta\:\mathrm{sin}\:\angle{A}\right)}×\sqrt{{u}^{\mathrm{2}} +{v}^{\mathrm{2}} +{z}^{\mathrm{2}} } \\ $$$$\mid\boldsymbol{{p}}×\boldsymbol{{q}}\mid=\frac{{bch}^{\mathrm{2}} \mathrm{sin}\:\angle{A}\sqrt{\left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} \right)\gamma^{\mathrm{2}} +\left(\mathrm{1}+\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} \right)^{\mathrm{2}} }}{\mathrm{2}\left({h}−\alpha{b}\right)\left[{h}−{c}\left(\alpha\:\mathrm{cos}\:\angle{A}+\beta\:\mathrm{sin}\:\angle{A}\right)\right]} \\ $$$$\mid\boldsymbol{{p}}×\boldsymbol{{q}}\mid=\frac{{h}^{\mathrm{2}} \Delta\sqrt{\left(\mathrm{1}−\gamma^{\mathrm{2}} \right)\gamma^{\mathrm{2}} +\left(\mathrm{2}−\gamma^{\mathrm{2}} \right)^{\mathrm{2}} }}{\left({h}−\alpha{b}\right)\left[{h}−{c}\left(\alpha\:\mathrm{cos}\:\angle{A}+\beta\:\mathrm{sin}\:\angle{A}\right)\right]} \\ $$$$\mid\boldsymbol{{p}}×\boldsymbol{{q}}\mid=\frac{\Delta\sqrt{\mathrm{1}+\mathrm{3}\alpha^{\mathrm{2}} +\mathrm{3}\beta^{\mathrm{2}} }}{\left(\mathrm{1}−\frac{{b}}{{h}}\alpha\right)\left[\mathrm{1}−\frac{{c}}{{h}}\left(\alpha\:\mathrm{cos}\:\angle{A}+\beta\:\mathrm{sin}\:\angle{A}\right)\right]} \\ $$$${let}\:\frac{{b}}{{h}}={l},\:\frac{{c}\:\mathrm{cos}\:\angle{A}}{{h}}={m},\:\frac{{c}\:\mathrm{sin}\:\angle{A}}{{h}}={n} \\ $$$${area}\:{of}\:{shadow}\:{A}=\frac{\Delta\sqrt{\mathrm{1}+\mathrm{3}\alpha^{\mathrm{2}} +\mathrm{3}\beta^{\mathrm{2}} }}{\left(\mathrm{1}−{l}\alpha\right)\left(\mathrm{1}−{m}\alpha−{n}\beta\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\sqrt{\Phi}\Delta\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\Phi=\frac{\mathrm{1}+\mathrm{3}\alpha^{\mathrm{2}} +\mathrm{3}\beta^{\mathrm{2}} }{\left(\mathrm{1}−{l}\alpha\right)^{\mathrm{2}} \left(\mathrm{1}−{m}\alpha−{n}\beta\right)^{\mathrm{2}} } \\ $$$$….. \\ $$
