Question Number 136417 by I want to learn more last updated on 21/Mar/21

Answered by EDWIN88 last updated on 22/Mar/21
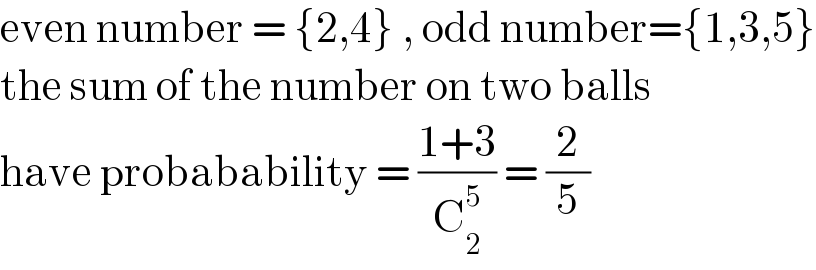
$$\mathrm{even}\:\mathrm{number}\:=\:\left\{\mathrm{2},\mathrm{4}\right\}\:,\:\mathrm{odd}\:\mathrm{number}=\left\{\mathrm{1},\mathrm{3},\mathrm{5}\right\} \\ $$$$\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{number}\:\mathrm{on}\:\mathrm{two}\:\mathrm{balls} \\ $$$$\mathrm{have}\:\mathrm{probabability}\:=\:\frac{\mathrm{1}+\mathrm{3}}{\mathrm{C}_{\mathrm{2}} ^{\mathrm{5}} }\:=\:\frac{\mathrm{2}}{\mathrm{5}} \\ $$
Answered by nadovic last updated on 22/Mar/21

$${The}\:{sum}\:{will}\:{be}\:{even}\:{if}\:{and}\:{only}\:{if}\: \\ $$$${both}\:{numbers}\:{are}\:{even}\:{or}\:{both}\:{are}\:{odd}. \\ $$$$\overset{} {\mathrm{S}ample}\:\mathrm{Space},\:{S}\:=\:\left\{\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:\mathrm{4},\:\mathrm{5}\right\} \\ $$$$\mathrm{Odd}\:\mathrm{numbers},\:{D}\:=\:\left\{\mathrm{1},\:\mathrm{3},\:\mathrm{5}\right\} \\ $$$$\underset{} {\mathrm{E}ven}\:\mathrm{numbers},\:{E}\:=\:\left\{\mathrm{2},\:\mathrm{4}\right\} \\ $$$$\:\:\left({a}\right)\:\mathrm{P}\left({sum}\:{is}\:{even}\right)\:=\:\frac{\mathrm{C}_{\mathrm{2}} +^{\mathrm{2}} \mathrm{C}_{\mathrm{2}} }{\mathrm{C}_{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\frac{\mathrm{2}}{\mathrm{5}} \\ $$$$\:\:\left({b}\right)\:\mathrm{Even}\:\mathrm{Sum},\:{V}\:=\:\left\{\mathrm{4},\:\mathrm{6},\:\mathrm{8}\right\} \\ $$$$\:\:\:\:\:\:\:\:\:{E}\cap{V}\:=\:\left\{\mathrm{4}\right\} \\ $$$$\Rightarrow\:\:\:\:\mathrm{P}\left({E}/{V}\right)\:=\:\:\frac{{n}\left({E}\cap{V}\right)}{{n}\left({V}\right)} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{P}\left({E}/{V}\right)\:=\:\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$
