Question Number 136445 by aupo14 last updated on 22/Mar/21
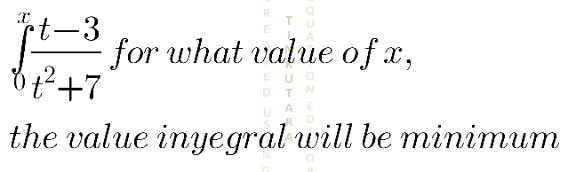
Answered by liberty last updated on 22/Mar/21
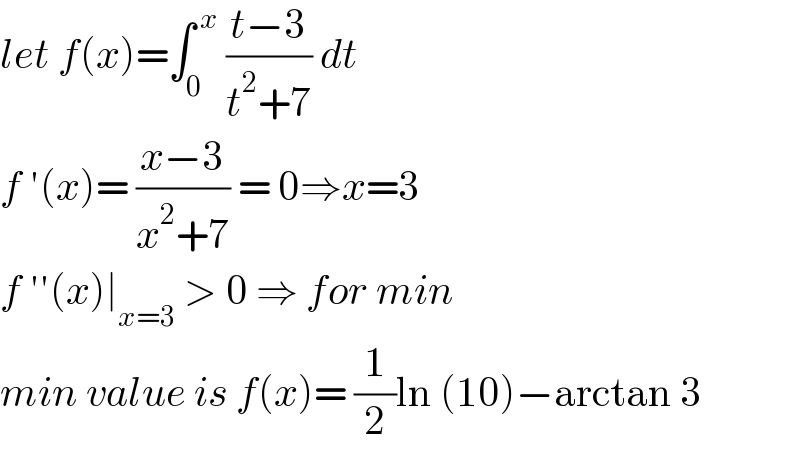
$${let}\:{f}\left({x}\right)=\int_{\mathrm{0}} ^{\:{x}} \:\frac{{t}−\mathrm{3}}{{t}^{\mathrm{2}} +\mathrm{7}}\:{dt}\: \\ $$$${f}\:'\left({x}\right)=\:\frac{{x}−\mathrm{3}}{{x}^{\mathrm{2}} +\mathrm{7}}\:=\:\mathrm{0}\Rightarrow{x}=\mathrm{3} \\ $$$${f}\:''\left({x}\right)\mid_{{x}=\mathrm{3}} \:>\:\mathrm{0}\:\Rightarrow\:{for}\:{min} \\ $$$${min}\:{value}\:{is}\:{f}\left({x}\right)=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left(\mathrm{10}\right)−\mathrm{arctan}\:\mathrm{3} \\ $$
Commented by aupo14 last updated on 22/Mar/21
can you give me the way you integrate it? im having a bit trouble
Commented by mr W last updated on 22/Mar/21
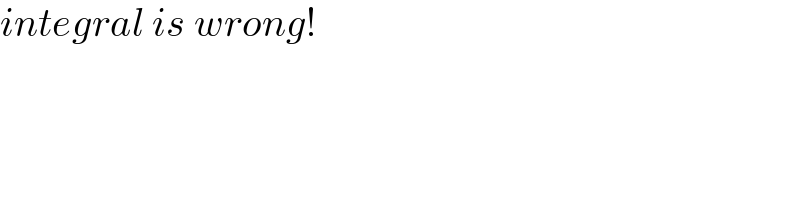
$${integral}\:{is}\:{wrong}! \\ $$
Commented by liberty last updated on 22/Mar/21
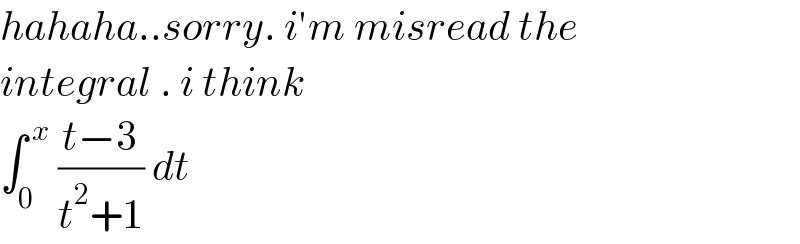
$${hahaha}..{sorry}.\:{i}'{m}\:{misread}\:{the} \\ $$$${integral}\:.\:{i}\:{think} \\ $$$$\int_{\mathrm{0}} ^{\:{x}} \:\frac{{t}−\mathrm{3}}{{t}^{\mathrm{2}} +\mathrm{1}}\:{dt} \\ $$
Answered by mr W last updated on 22/Mar/21
![f(x)=∫_0 ^x ((t−3)/(t^2 +7))dt =∫_0 ^x [(t/(t^2 +7))−(3/(t^2 +7))]dt =(1/2)∫_0 ^x ((d(t^2 +7))/(t^2 +7))−3∫_0 ^x (dt/(t^2 +7)) =(1/2)[ln (t^2 +7)]_0 ^x −(3/( (√7)))[tan^(−1) (t/( (√7)))]_0 ^x =(1/2)ln ((x^2 +7)/7)−(3/( (√7))) tan^(−1) (x/( (√7))) f′(x)=((x−3)/(x^2 +7))=0 ⇒x=3 f(x)_(min) =f(3)=(1/2)ln ((16)/7)−(3/( (√7)))tan^(−1) (3/( (√7)))≈−0.548](https://www.tinkutara.com/question/Q136459.png)
$${f}\left({x}\right)=\int_{\mathrm{0}} ^{{x}} \frac{{t}−\mathrm{3}}{{t}^{\mathrm{2}} +\mathrm{7}}{dt} \\ $$$$\:\:\:\:\:\:\:\:\:=\int_{\mathrm{0}} ^{{x}} \left[\frac{{t}}{{t}^{\mathrm{2}} +\mathrm{7}}−\frac{\mathrm{3}}{{t}^{\mathrm{2}} +\mathrm{7}}\right]{dt} \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{{x}} \frac{{d}\left({t}^{\mathrm{2}} +\mathrm{7}\right)}{{t}^{\mathrm{2}} +\mathrm{7}}−\mathrm{3}\int_{\mathrm{0}} ^{{x}} \frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{7}} \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{ln}\:\left({t}^{\mathrm{2}} +\mathrm{7}\right)\right]_{\mathrm{0}} ^{{x}} −\frac{\mathrm{3}}{\:\sqrt{\mathrm{7}}}\left[\mathrm{tan}^{−\mathrm{1}} \frac{{t}}{\:\sqrt{\mathrm{7}}}\right]_{\mathrm{0}} ^{{x}} \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\frac{{x}^{\mathrm{2}} +\mathrm{7}}{\mathrm{7}}−\frac{\mathrm{3}}{\:\sqrt{\mathrm{7}}}\:\mathrm{tan}^{−\mathrm{1}} \frac{{x}}{\:\sqrt{\mathrm{7}}} \\ $$$${f}'\left({x}\right)=\frac{{x}−\mathrm{3}}{{x}^{\mathrm{2}} +\mathrm{7}}=\mathrm{0}\:\Rightarrow{x}=\mathrm{3} \\ $$$${f}\left({x}\right)_{{min}} ={f}\left(\mathrm{3}\right)=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\frac{\mathrm{16}}{\mathrm{7}}−\frac{\mathrm{3}}{\:\sqrt{\mathrm{7}}}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{3}}{\:\sqrt{\mathrm{7}}}\approx−\mathrm{0}.\mathrm{548} \\ $$
