Question Number 136537 by Jamshidbek last updated on 23/Mar/21
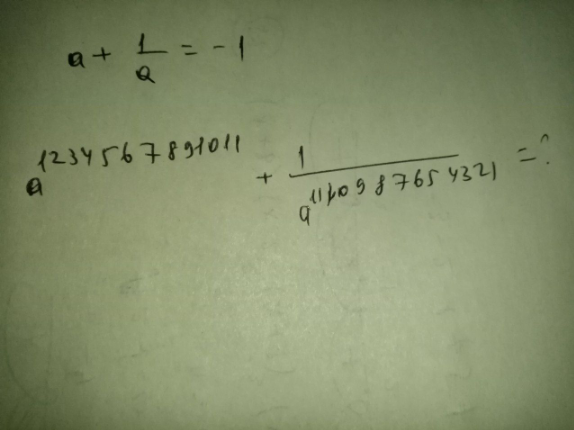
Answered by Olaf last updated on 23/Mar/21

$${a}+\frac{\mathrm{1}}{{a}}\:=\:−\mathrm{1} \\ $$$${a}^{\mathrm{2}} +{a}+\mathrm{1}\:=\:\mathrm{0} \\ $$$${a}\:=\:\frac{−\mathrm{1}\pm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:=\:{e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \mathrm{or}\:{e}^{{i}\frac{\mathrm{4}\pi}{\mathrm{3}}} \\ $$$$\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}+\mathrm{5}+\mathrm{6}+\mathrm{7}+\mathrm{8}+\mathrm{9}+\mathrm{1}+\mathrm{0}+\mathrm{1}+\mathrm{1} \\ $$$$=\:\frac{\mathrm{9}×\mathrm{10}}{\mathrm{2}}+\mathrm{3}\:=\:\mathrm{48}\:=\:\mathrm{3}{n}\:\left({n}\:=\:\mathrm{16}\right) \\ $$$$\Rightarrow\:\mathrm{1234567891011}\:=\:\mathrm{3}{p},\:{p}\in\mathbb{N} \\ $$$$\mathrm{and}\:\mathrm{1110987654321}\:=\:\mathrm{3}{q},\:{q}\in\mathbb{N} \\ $$$$\mathrm{If}\:{a}\:=\:{e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \:: \\ $$$${a}^{\mathrm{1234567891011}} +\frac{\mathrm{1}}{{a}^{\mathrm{1110987654321}} } \\ $$$$=\:{a}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}×\mathrm{3}{p}} +\frac{\mathrm{1}}{{e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}×\mathrm{3}{q}} }\:=\:{e}^{\mathrm{2}{p}\pi{i}} +{e}^{−\mathrm{2}{q}\pi{i}} \:=\:\mathrm{2} \\ $$$$\mathrm{If}\:{a}\:=\:{e}^{{i}\frac{\mathrm{4}\pi}{\mathrm{3}}} \:: \\ $$$$=\:{a}^{{i}\frac{\mathrm{4}\pi}{\mathrm{3}}×\mathrm{3}{p}} +\frac{\mathrm{1}}{{e}^{{i}\frac{\mathrm{4}\pi}{\mathrm{3}}×\mathrm{3}{q}} }\:=\:{e}^{\mathrm{4}{p}\pi{i}} +{e}^{−\mathrm{4}{q}\pi{i}} \:=\:\mathrm{2} \\ $$$$\mathrm{answer}\:\mathrm{is}\::\:\mathrm{2} \\ $$
Commented by Jamshidbek last updated on 23/Mar/21

$${thank}\:{you}\:{sir} \\ $$
