Question Number 136651 by mhabs last updated on 24/Mar/21
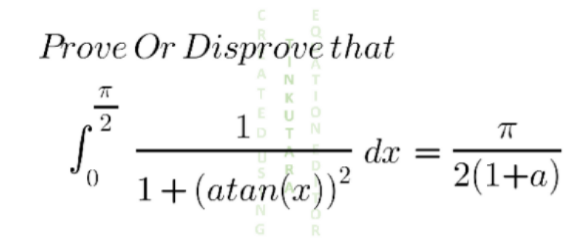
Answered by Ñï= last updated on 24/Mar/21
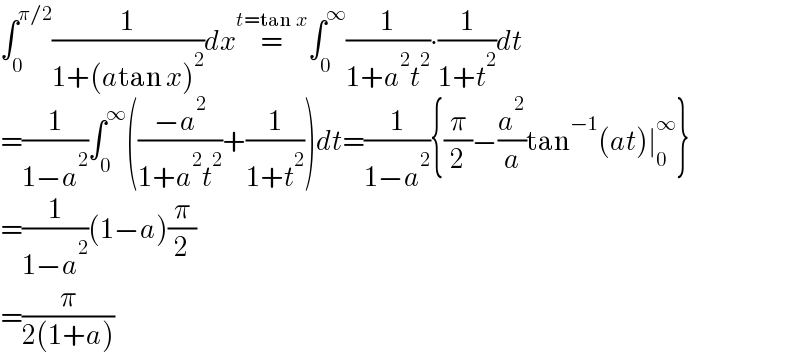
$$\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{\mathrm{1}}{\mathrm{1}+\left({a}\mathrm{tan}\:{x}\right)^{\mathrm{2}} }{dx}\overset{{t}=\mathrm{tan}\:{x}} {=}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{1}+{a}^{\mathrm{2}} {t}^{\mathrm{2}} }\centerdot\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}−{a}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} \left(\frac{−{a}^{\mathrm{2}} }{\mathrm{1}+{a}^{\mathrm{2}} {t}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }\right){dt}=\frac{\mathrm{1}}{\mathrm{1}−{a}^{\mathrm{2}} }\left\{\frac{\pi}{\mathrm{2}}−\frac{{a}^{\mathrm{2}} }{{a}}\mathrm{tan}^{−\mathrm{1}} \left({at}\right)\mid_{\mathrm{0}} ^{\infty} \right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}−{a}^{\mathrm{2}} }\left(\mathrm{1}−{a}\right)\frac{\pi}{\mathrm{2}} \\ $$$$=\frac{\pi}{\mathrm{2}\left(\mathrm{1}+{a}\right)} \\ $$
Answered by Dwaipayan Shikari last updated on 24/Mar/21
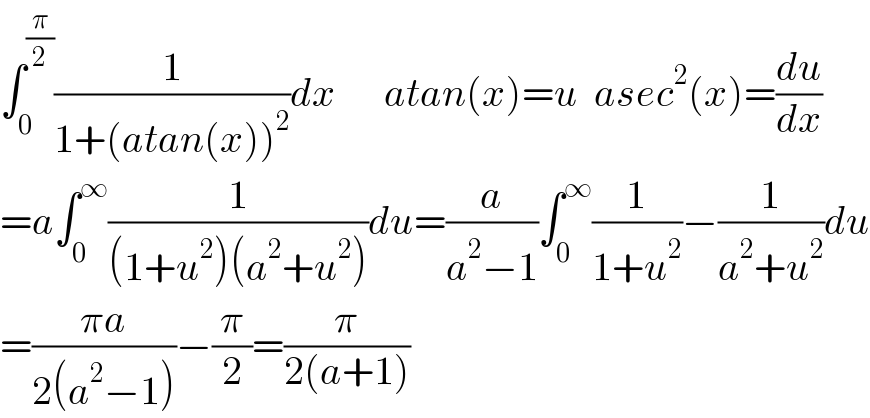
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{\mathrm{1}+\left({atan}\left({x}\right)\right)^{\mathrm{2}} }{dx}\:\:\:\:\:\:{atan}\left({x}\right)={u}\:\:{asec}^{\mathrm{2}} \left({x}\right)=\frac{{du}}{{dx}} \\ $$$$={a}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\left({a}^{\mathrm{2}} +{u}^{\mathrm{2}} \right)}{du}=\frac{{a}}{{a}^{\mathrm{2}} −\mathrm{1}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }−\frac{\mathrm{1}}{{a}^{\mathrm{2}} +{u}^{\mathrm{2}} }{du} \\ $$$$=\frac{\pi{a}}{\mathrm{2}\left({a}^{\mathrm{2}} −\mathrm{1}\right)}−\frac{\pi}{\mathrm{2}}=\frac{\pi}{\mathrm{2}\left({a}+\mathrm{1}\right)} \\ $$
