Question Number 136656 by 0731619177 last updated on 24/Mar/21
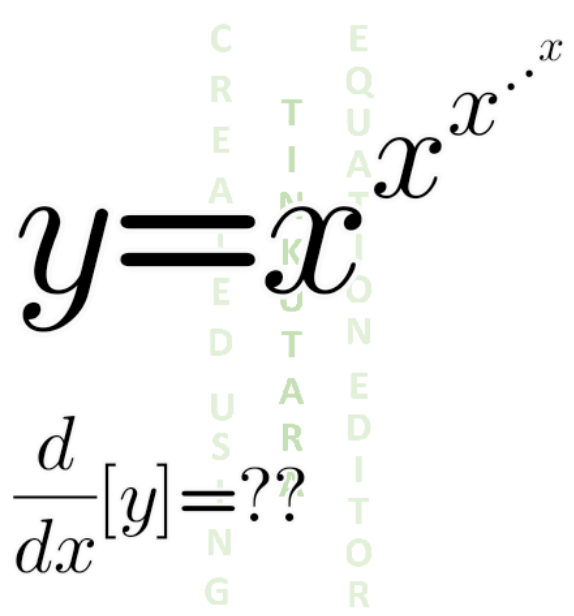
Answered by Ñï= last updated on 24/Mar/21
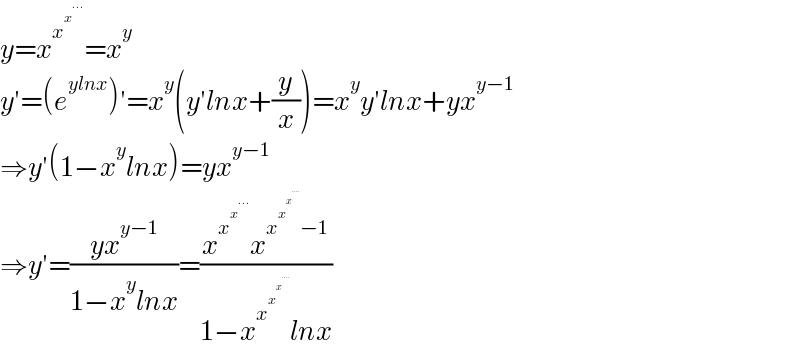
$${y}={x}^{{x}^{{x}^{…} } } ={x}^{{y}} \\ $$$${y}'=\left({e}^{{ylnx}} \right)'={x}^{{y}} \left({y}'{lnx}+\frac{{y}}{{x}}\right)={x}^{{y}} {y}'{lnx}+{yx}^{{y}−\mathrm{1}} \\ $$$$\Rightarrow{y}'\left(\mathrm{1}−{x}^{{y}} {lnx}\right)={yx}^{{y}−\mathrm{1}} \\ $$$$\Rightarrow{y}'=\frac{{yx}^{{y}−\mathrm{1}} }{\mathrm{1}−{x}^{{y}} {lnx}}=\frac{{x}^{{x}^{{x}^{…} } } {x}^{{x}^{{x}^{{x}^{….} } } −\mathrm{1}} }{\mathrm{1}−{x}^{{x}^{{x}^{{x}^{….} } } } {lnx}} \\ $$
Commented by 0731619177 last updated on 24/Mar/21

$${thanks} \\ $$
Commented by snipers237 last updated on 24/Mar/21
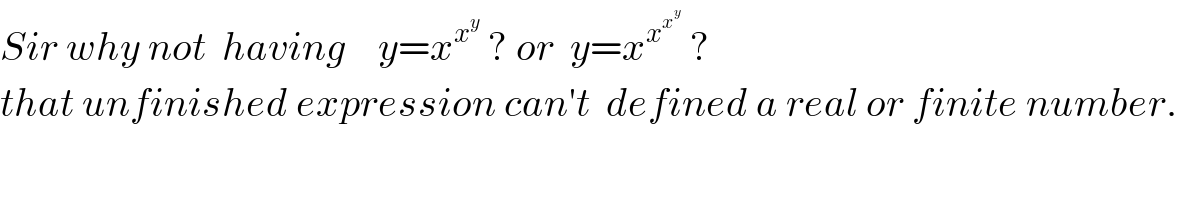
$${Sir}\:{why}\:{not}\:\:{having}\:\:\:\:{y}={x}^{{x}^{{y}} } \:?\:{or}\:\:{y}={x}^{{x}^{{x}^{{y}} } } \:? \\ $$$${that}\:{unfinished}\:{expression}\:{can}'{t}\:\:{defined}\:{a}\:{real}\:{or}\:{finite}\:{number}. \\ $$
Commented by MJS_new last updated on 25/Mar/21
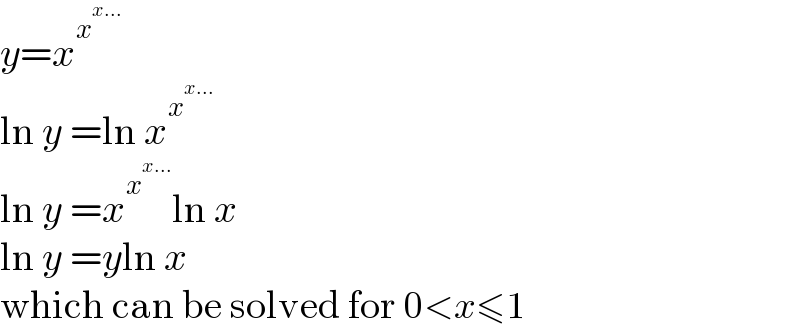
$${y}={x}^{{x}^{{x}…} } \\ $$$$\mathrm{ln}\:{y}\:=\mathrm{ln}\:{x}^{{x}^{{x}…} } \\ $$$$\mathrm{ln}\:{y}\:={x}^{{x}^{{x}…} } \mathrm{ln}\:{x} \\ $$$$\mathrm{ln}\:{y}\:={y}\mathrm{ln}\:{x} \\ $$$$\mathrm{which}\:\mathrm{can}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{for}\:\mathrm{0}<{x}\leqslant\mathrm{1} \\ $$
Commented by snipers237 last updated on 24/Mar/21
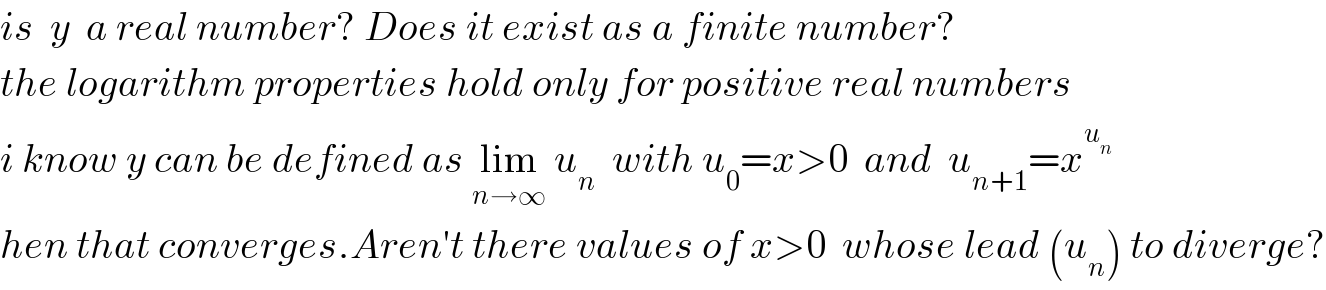
$${is}\:\:{y}\:\:{a}\:{real}\:{number}?\:{Does}\:{it}\:{exist}\:{as}\:{a}\:{finite}\:{number}? \\ $$$${the}\:{logarithm}\:{properties}\:{hold}\:{only}\:{for}\:{positive}\:{real}\:{numbers} \\ $$$${i}\:{know}\:{y}\:{can}\:{be}\:{defined}\:{as}\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{u}_{{n}} \:\:{with}\:{u}_{\mathrm{0}} ={x}>\mathrm{0}\:\:{and}\:\:{u}_{{n}+\mathrm{1}} ={x}^{{u}_{{n}} } \:\:\: \\ $$$${hen}\:{that}\:{converges}.{Aren}'{t}\:{there}\:{values}\:{of}\:{x}>\mathrm{0}\:\:{whose}\:{lead}\:\left({u}_{{n}} \right)\:{to}\:{diverge}? \\ $$
