Question-136670

Question Number 136670 by rexford last updated on 24/Mar/21

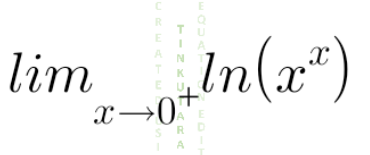
Answered by Dwaipayan Shikari last updated on 24/Mar/21

0

Answered by MJS_new last updated on 24/Mar/21

\ln x^{x} = x \ln x \forall x > 0

\lim_{x \to 0^{+}} x \ln x = \lim_{t \to + \infty} \frac{\ln \frac{1}{t}}{t} = - \lim_{t \to + \infty} \frac{\ln t}{t} =

= - \lim_{t \to + \infty} \frac{\frac{d}{d t} [\ln t]}{\frac{d}{d t} [t]} = - \lim_{t \to + \infty} \frac{\frac{1}{t}}{1} = 0

Commented by rexford last updated on 24/Mar/21

t h a n k s v e r y m u c h f o r y o u r t i m e

Facebook Tweet Pin